Lecture 72 - Monoidal Categories

Lecture 72 - Monoidal Categories

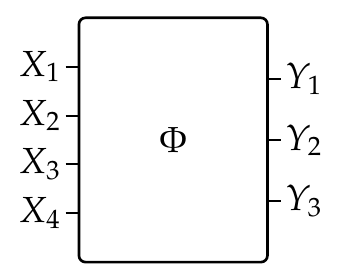
In the last few lectures, we have seen how to describe complex systems made out of many parts. Each part has abstract wires coming in from the left standing for 'requirements' - things you might want it to do - and from the right standing for 'resources' - things you might need to give it, so it can do what you want:

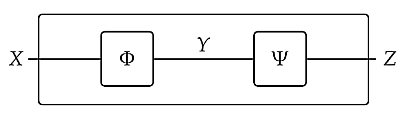
We've seen that these parts can be stuck together in series, by 'composition':

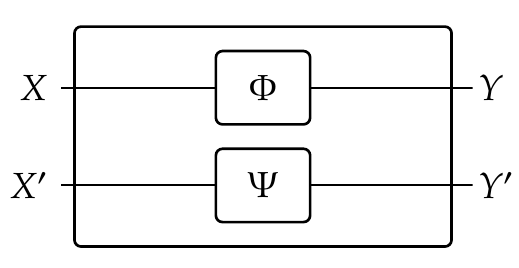
and in parallel, using 'tensoring':

One reason I wanted to show you this is for you to practice reasoning with diagrams in situations where you can both compose and tensor morphisms. Examples include:

The kind of structure where you can compose and tensor morphisms is called a 'monoidal category'. This is a category \(\mathcal{C}\) together with:

[ \alpha_{X,Y,Z} \colon (X \otimes Y) \otimes Z \stackrel{\sim}{\longrightarrow} X \otimes (Y \otimes Z) ]

[ \lambda_X \colon I \otimes X \stackrel{\sim}{\longrightarrow} X ]

[ \rho_x \colon X \otimes I \stackrel{\sim}{\longrightarrow} X ]

We need the associator and unitors because in examples it's usually not true that \( (X \otimes Y) \otimes Z\) is equal to \(X \otimes (Y \otimes Z)\), etc. They're just isomorphic! But we want the associator and unitors to obey equations because they're just doing boring stuff like moving parentheses around, and if we use them in two different ways to go from, say,

[ ((W \otimes X) \otimes Y) \otimes Z) ]

to

[ W \otimes (X \otimes (Y \otimes Z)) ]

we want those two ways to agree! Otherwise life would be too confusing.

If you want to see exactly what equations the associator and unitors should obey, read this:

But beware: these equations, discovered by Mac Lane in 1963, are a bit scary at first! They say that certain diagrams built using tensoring, the associator and unitors commute, and the point is that Mac Lane proved a theorem saying these are enough to imply that all diagrams of this sort commute.

This result called 'Mac Lane's coherence theorem'. It's rather subtle; if you're curious about the details try this:

Note: monoidal categories may not necessarily have a natural isomorphism

[ \beta_{X,Y} \colon X \otimes Y \stackrel{\sim}{\longrightarrow} Y \otimes X .]

When we have that, obeying some more equations, we have a 'braided monoidal category'. You can see the details in my notes. And when our braided monoidal category has the feature that braiding twice:

[ X\otimes Y \stackrel{\beta_{X,Y}}{\longrightarrow } Y \otimes X \stackrel{\beta_{Y,X}}{\longrightarrow } X \otimes Y ]

is the identity, we have a 'symmetric monoidal category'. In this case we call the braiding a symmetry and often write it as

[ \sigma_{X,Y} \colon X \otimes Y \stackrel{\sim}{\longrightarrow} Y \otimes X ]

since the letter \(\sigma\) should make you think 'symmetry'.

All the examples of monoidal categories I listed are actually symmetric monoidal - unless you think of circuit diagrams as having wires in 3d space that can actually get tangled up with each other, in which case they are morphisms in a braided monoidal category.

Puzzle 278. Use the definition of monoidal category to prove the interchange law

[ (f \otimes g) (f' \otimes g') = ff' \otimes gg' ]

whenever \(f,g,f',g'\) are morphsms making either side of the equation well-defined. (Hint: you only need the part of the definition I explained in my lecture, not the scary diagrams I didn't show you.)

Puzzle 279. Draw a picture illustrating this equation.

Puzzle 280. Suppose \(f : I \to I\) and \(g : I \to I\) are morphisms in a monoidal category going from the unit object to itself. Show that

[ fg = gf .]

To read other lectures go here.

© 2018 John Baez