John Baez

Algebraic Topological Methods in Computer Science 2008, University of Paris Diderot (Paris 7)

July 7, 2008

Computation and the Periodic Table

By now there is an extensive network of interlocking analogies between physics, topology, logic and computer science, which can be seen most easily by comparing the roles that symmetric monoidal closed categories play in each subject. However, symmetric monoidal categories are just the n = 1, k = 3 entry of a hypothesized "periodic table" of k-tuply monoidal n-categories. This raises the question of how these analogies extend. 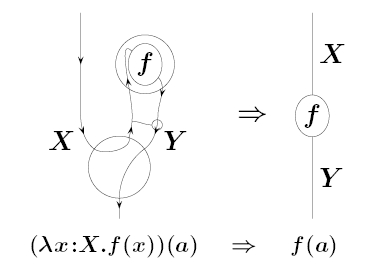We present some thoughts on this question, focusing on how symmetric monoidal closed 2-categories might let us understand the lambda calculus more deeply. This is based on work in progress with Mike Stay.

Click on this to see the transparencies of the talk:

• Computation and the Periodic Table - in PDF and Postscript

• John Baez and James Dolan, Higher-dimensional algebra and topological quantum field theory, J. Math. Phys. 36 (1995), 6073-6105.

• John Baez and Laurel Langford, Higher-dimensional algebra IV: 2-tangles, Adv. Math. 180 (2003), 705-764.

• John Baez and Mike Stay, Physics, topology, logic and computation: a Rosetta Stone, to appear in New Structures in Physics, ed. Bob Coecke.

• Albert Burroni, Higher-dimensional word problems with applications to equational logic, Theor. Comp. Sci. 115 (1993), 43-62.

• Yves Guiraud, The three dimensions of proofs, Ann. Pure Appl. Logic 141 (2006), 266-295.

• Barnaby P. Hilken, Towards a proof theory of rewriting: the simply-typed 2λ-calculus, Theor. Comp. Sci. 170 (1996), 407-444.

• C. Barry Jay and Neil Ghani, The virtues of eta-expansion, J. Functional Programming 1 (1993), 1-19.

• R. A. G. Seely, Weak adjointness in proof theory in Proc. Durham Conf. on Applications of Sheaves, Springer Lecture Notes in Mathematics 753, Springer, Berlin, 1979, pp. 697-701.

• R. A. G. Seely, Modeling computations: a 2-categorical framework, in Proc. Symposium on Logic in Computer Science 1987, Computer Society of the IEEE, pp. 65-71.

• Vladimir Voevodsky, A very short note on the homotopy lambda calculus, Sept. 27, 2006.

home