The Conway Polynomial

These days I'm mainly working on the relationship of braids and quantization. Lots of people are interested in that these days, but lots more aren't, I bet, so let me briefly explain just a bit...

There's a knot invariant called the Conway polynomial that may be defined by essentially two rules. It's a polynomial in one variable, say $z$; let's call the polynomial assigned to the knot (or link) $K$, $\nabla(K)$. The knot $K$ has to be oriented; that is, one must draw little arrows tangent to it that say which way to go: $\to$. Okay:

Rule 1: If $K$ is the unknot (an unknotted circle), $\nabla(K) = 1$. This is sort of a normalization rule.

Rule 2: Suppose $K$, $K'$, and $L$ are 3 knots (or links) differing at just one crossing (we're supposing them to be drawn as pictures in 2 dimensions).

At this crossing they look as follows:

$K$ looks like:

$K'$ looks like:

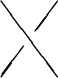
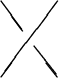
$L$ looks like:

(All of them should have arrows pointing down. Any rotated version of this picture is fine too -- this is topology, after all!)

Then we have the ``skein relation''

$$\nabla(K) - \nabla(K') = z\nabla(L) .$$

It was Louis Kauffman, I believe, who first noted that this looks a lot like the famous canonical commutation relations, or Heisenberg relations:

$$pq - qp = -i \hbar$$

(Here $p$ is momentum, $q$ is position, and $\hbar$ is Planck's constant). Of course it looks more like it if you call the variable $z$ ``$\hbar$'', but the real thing is to note that the two kinds of crossings in $K$ and $K'$ are analogous (somehow) to the different orderings in $pq$ and $qp$.

Well, one could easily laugh this off as the ravings of someone who has been studying knot theory for too long, but it turned out that there was a deep connection. It was Turaev who first gave a precise formulation. He constructed an algebra from knots that involved a variable, $\hbar$, and such that as $\hbar \rightarrow 0$ it converged (in some sense) to an algebra of loops on a two-dimensional surface. Projected onto a two-dimensional surface the knots $K$ and $K'$ are the same, of course, so this makes some sense.

This however was only the tip of the iceberg...

© 1992 John Baez
baez@math.removethis.ucr.andthis.edu

home