r-Algebras

So...let's say we have an r-algebra. That's an algebra with an invertible linear map $R: A\otimes A \rightarrow A\otimes A$, which we draw as a right-crossing:

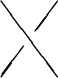
which satisfies 1) the Yang-Baxter equations:

2) $R(1\otimes a) = a\otimes 1$ and $R(a\otimes 1) = 1\otimes a$,

and 3) the quasitriangularity conditions; writing multiplication as the joining of strands these are

and

We say an r-algebra is "r-commutative" if

and "strong" if $R^2$ is the identity, or $R$ equals its inverse, i.e.:

(Note that a left-crossing

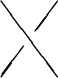
is the inverse of a right-crossing.)

All sorts of noncommutative analogs of manifolds are r-commutative algebras: quantum groups, noncommutative tori, quantum vector spaces, the Weyl and Clifford algebras, certain universal enveloping algebras, supermanifolds, etc. It seems that the ones with direct relevance to quantum theory in 4 dimensions are "strong," while the non-strong ones, like quantum groups, are primarily relevant to 2- and 3-dimensional physics. I would now like to describe an analog of differential forms for strong r-commutative algebras, and illustrate it for the case of the Heisenberg algebra -- i.e., the algebra defined by the canonical commutation relations: $pq - qp = -i \hbar$.

What are differential forms? Of course, they're the basis of a lot of differential geometry, and there are lots of equivalent ways of defining them, but let me take an algebraic viewpoint. Let $A$ be the algebra of smooth functions on a manifold $M$. We define differential forms as follows. Each function $f$ in $A$ has a "differential" $df$, and the functions and their differentials generate an algebra in which we impose the following relations:

1. Linearity: $d(f+g) = df + dg$, $d(cf) = c(df)$ for any scalar $c$.

2. The product rule: $d(fg) = (df)g + f(dg)$.

3. The derivative of a constant vanishes: $d1 = 0$.

4. Commutation relations: $f(dg) = (dg)f$ and $(df)(dg) = -(dg)(df)$.

This algebra is called the algebra of differential forms on $M$.

That's all, folks! If you've taken a course in differential geometry you were probably exposed to tangent planes and all that stuff, but if you want to get calculating with differential forms as soon as possible this is all you need to start with.

Note that rule 4) is the only one in which we switch elements of $A$ -- moving $f$ to the right of $g$. This is the rule we'll need to modify for an r-commutative algebra. You could, of course, just leave out rule 4): given any algebra $A$, the algebra whose relations are just given by 1)-3) is called the "universal differential calculus" for $A$. It's a reasonable substitute for differential forms when $A$ is any old noncommutative algebra, and (from one viewpoint) it's the basis of Alain Connes' approach to noncommutative differential geometry. But when you have a strong r-commutative algebra one can replace rule 3) with

4$'$) Commutation relations: $f(dg) = (dg^i)f_i$ and $(df)(dg) = -(dg^i)(df_i)$.

Here I should explain that I'm writing $R(f\otimes g)$ as the sum over $i$ of tensor products of the form $g^i\otimes f_i$ (one can always do this), and I'm using the Einstein summation convention (sum over repeated indices) to avoid writing the summation sign. What we're doing in rule 4$'$) is just what we should do: use $R$ to "switch" $f$ and $g$ instead of "naively" switching them as in 4).

Now let me show what this buys you in the case of the Heisenberg algebra. This is the algebra over $C$ generated by 3 formal variables, $p$, $q$, and $h$, subject to the relations that

$$pq - qp = -ih^2$$

$$ph =hp$$

$$qh=hq$$

Note that we're not treating $h$ as a number here, but as a variable, so I have to explicitly say that it commutes with everything. (If $h$ were a number, it would be $\sqrt{\hbar}$.)

This algebra is actually a strong r-commutative algebra in a unique manner such that

$$R(p\otimes h) = h\otimes p$$

$$R(q\otimes h) = h\otimes q$$

and

$$R(p\otimes q) = q\otimes p - i h\otimes h$$

Note what these say: the first two say that you switch $h$ with $p$ and $q$ in the usual way, and the third one says that when you switch $p$ and $q$, you get the expected term and then a piece, $-i h\otimes h$, which comes from the fact that $p$ and $q$ don't commute. The point is that while the Heisenberg algebra is not commutative, the canonical commutations relations do tell you exactly what to do when you switch $p$ and $q$, which is just as good!

If I may digress...I happen to have the paper by Heisenberg, Born, and Jordan with me, "Zur Quantenmechanik II", published in 1926, in which the canonical commutation relations are introduced. I quote:

Das Rechnen mit den quantentheoretischen Grössen würde wegen der Nichtgültigkeit des kommutativen Gesetzes der Multiplikation in gewissem Sinne unbestimmt bleiben, wenn nicht der Wert von $pq - qp$ vorgeschrieben würde. Wir führen daher als fundamentale quantenmechanische Relation ein:

$$pq - qp = (\frac{h}{2\pi i}){\bf 1}.$$

or if your German is rusty:

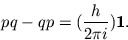
`Due to the failure of the commutative law for multiplication, computations with quantum-theoretical quantities are ambiguous in a certain sense, unless one prescribes a value for $pq - qp$. We introduce accordingly the following as the fundamental quantum-mechanical relation:

$$pq - qp = (\frac{h}{2\pi i}){\bf 1}.$$

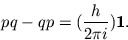
Ain't that cool? Anyway, we take the Heisenberg algebra as a strong r-commutative algebra and define the differential forms on this algebra by the rules 1), 2) and 3'), we get the following standard-looking relations:

$$\begin{array}{llll} h dp = dp h, & h dq = dq h, & p\... ...h = dh h, & p dp = dp p, & q dq = dq q\\ \end{array}$$

and a bunch of similar ones involving two differentials:

$$\begin{array}{llll} dh dp = -dp dh, & dh dq = -dq dh... ...dq,\\ dh dh = 0, & dp dp = 0, & dq dq = 0\\ \end{array}$$

but then some more interesting ones:

$$\begin{array}{c} p dq - dq p = -ih dh\\ q dp - dp q = ih dh\\ dp dq = -dq dp \end{array}$$

It's a nice little exercise to see that these really do follow from 1)-4$'$). One can have fun doing various things with these "quantized differential forms" (and their generalizations), basically by taking your favorite facts from the differential geometry of phase space and trying to "quantize" them, but let me just briefly run through the basics. (Now I will let myself be more mathematical.) One may form a quotient of the Heisenberg algebra by specializing the variable $h$ to some value; this is called the Weyl algebra. The corresponding differential forms on the Weyl algebra were discovered by I. Segal some time ago and called "quantized differential forms;" their cohomology gives a nice way of understanding the Wick product in quantum field theory. (He also dealt with a fermionic version using the Clifford algebra.) In my paper on r-commutative geometry I recommend an approach in which one views the Heisenberg algebra as a "bundle" over the "line" whose coordinate is given by $h$. A given "fiber" (at which $h$ has some numerical value) is then a Weyl algebra (except for the "classical fiber" at $h= 0$, which is just the algebra of polynomials on phase space). I put quotes around the words "fiber bundle" because only the classical fiber is really a manifold; the rest are "quantum manifolds," i.e. noncommutative algebras. But the fiber bundle viewpoint gives good insight into the relation between the differential forms on the base (the line), the fibers (Weyl algebras) and the total space (the Heisenberg algebra). This viewpoint also works for noncommutative tori (and other cases). Neither of these examples are exciting from the point of view of braid invariants, since they are "strong". The differential forms as defined above do not work very well for non-strong r-algebras. I have no idea whether there is a good general definition of differential forms for r-commutative algebras; there is a definition that works for the quantum plane and other quantum vector spaces with Hecke-type relations (i.e., not $R^2 = 1$, but $R^2 = (1-q)R + q$.) I just finished writing a paper in which I define a generalization of Hochschild homology for r-algebras and relate it to the r-commutative differential forms defined above. This paper is available here:

• Hochschild homology in a braided tensor category, Trans. Amer. Math. Soc. 344 (1994), 885-906.

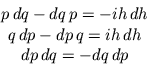
But if actually you want to read that, you probably should read this first:

• R-commutative geometry and quantization of Poisson algebras, Adv. Math. 95 (1992) 61 - 91.

© 1992 John Baez
baez@math.removethis.ucr.andthis.edu

home