

That's what the spacecraft Dawn said on Twitter today. After more than 7 years and a visit to the asteroid Vesta, Dawn has reached its goal!
I hope the white spots on Ceres are a solar power plant for an alien base, or at least a 'cryovolcano' — a volcano that shoots up liquid water instead of lava. But probably they're just ice or snow.
Still, this is pretty cool! Ceres is probably a protoplanet whose growth got stopped by the huge gravitational pull of Jupiter. We know it has water vapor in its tiny atmosphere. It may have a lot of ice inside, unlike most of the rocky asteroids. So we can learn a bit about how planets first formed by visiting this world.
It's also cool how we got there. NASA couldn't explore Ceres without ion propulsion. Dawn started out its journey with 425 kilograms of the noble gas xenon. It turns this gas into ions and shoots them out the back to accelerate through space. So, it rides through space on a blue-green beam of ions!
This is the kind of thing we can do if we stop fussing and fighting for a while. Are we really ready to explore the universe? Maybe not yet. But someday....

This is the kind of thruster that powered the spacecraft Dawn to the asteroids Vesta and Ceres. It's beautiful! It creates a beam of xenon ions. These ions blast into space at 40 kilometers per second — 90,000 miles per hour! — pushing the ship forward.
Dawn is solar powered. It sucks up 10 kilowatts of solar power and uses this to run the ion thruster. It started out with 275 kilograms of the noble gas xenon. It takes atoms of this gas and strips off some the electrons, leaving the atoms positively charged. These are called ions.
It accelerates these ions with an electric field, and they shoot out of thousands of tiny holes — which I think you can see here. Each hole acts as a lens that electrically focuses the ions.
Because the ion thruster puts out positive ions, an equal amount of negative charge must be expelled to keep the spacecraft from getting a huge electric charge. So, a small gadget called the 'neutralizer' shoots out electrons.
The force produced by Dawn's thrusters is tiny: just 40 millinewtons. A newton is the force it takes to accelerate one kilogram one meter per second each second. Dawn's thrusters push as hard as a sheet of paper pushes down on your hand!
So, this spacecraft takes four days to accelerate from 0 to 100 kilometers per hour, while a good car can do it in 3-6 seconds. The advantage of Dawn is that it can keep up this acceleration for years without running out of propellant. This is what made it the first spacecraft able to slow down and orbit one body in our Solar System, then take off and go to another, then slow down and orbit that!
Puzzle 1: Why does Dawn use xenon? Is it just because this gas has a really cool-sounding name?
Puzzle 2: What bad things might happen if Dawn built up a big electric charge?
Puzzle 3: Why does the ion beam glow? Why is it blue?
Puzzle 4: Another elegant form of propulsion is a solar sail, where sunlight pushes a spacecraft directly. Why isn't this better than converting sunlight to energy and using that to run an ion drive? After all, converting energy from one form to another tends to create waste heat.
For answers to these puzzles, see the comments on my G+ post.
The ancient game of go still holds many challenges. Compared to go, chess is like tac-tac-toe. There are 255168 possible games of tic-tac-toe. There are about 10120 possible chess games. But there are about 10761 possible go games!
The main challenge with go is playing it well. But there's also counting the number of legal positions.
A full-fledged go board has 19 × 19 squares, and approximately this many legal positions:
That's about 2 × 10170.
John Tromp wants to know the exact number. Why? Because it's a fun challenge. He knows an algorithm to calculate this number. It's very clever. But it still takes a lot of computing power.
He recently calculated the number of legal moves on an 18 × 18 board. It took 9 months, and 4 petabytes of disk IO on a Dell PowerEdge R820 server. He did it at the Institute for Advanced Studies in Princeton... that place where Einstein used to hang out. The answer is:
To get the answer for a 19 × 19 board will take more work. Using some very clever math, the task can be split up into 9 jobs that each compute 64 bits of the 566-bit result. To do this and be sure the answer is right, he needs about 10 to 13 servers, each with at least 8 cores, 512 gigabytes of RAM, and 10-15 terabytes of disk space. The job will take about 5-9 months.
You can read more about this here:
including the answers for all square boards of size up to 18 × 18. The most interesting part is the algorithm to compute these numbers:
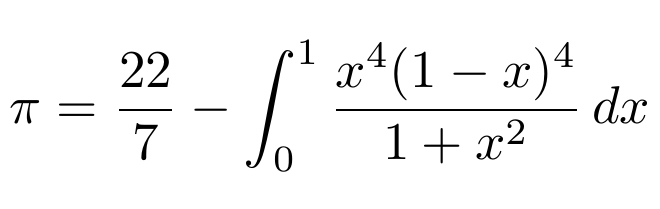
But getting into the silly spirit of things, consider this formula. It's true. But it's hilarious.
This is a famous approximation to pi:
The hilarious part is that the difference
is given by the elegant integral shown above!
This formula goes back at least to this paper:
• D. P. Dalzell, On 22/7, J. London Math. Soc. 19 (1944), 133–134,
Since the integrand is nonnegative, it gives a nice proof that pi is less than 22/7, and with a little more work you can use it to show that pi is more than
For more on this formula, including a proof, see:
and
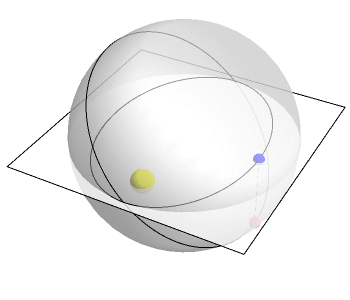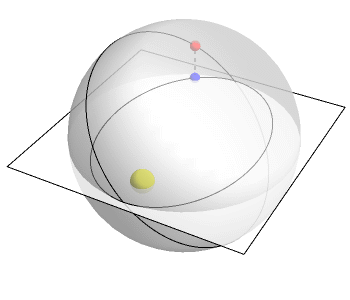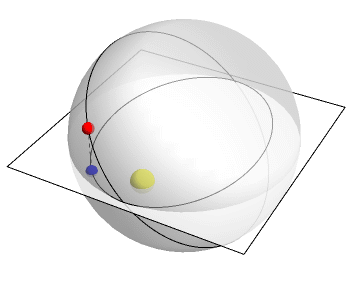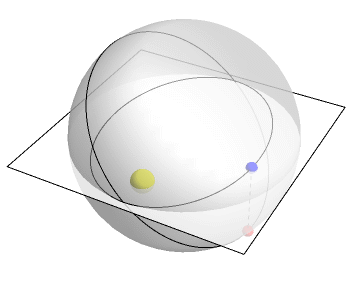
I bet you know that planets go around the sun in elliptical orbits. But do you know why?
In fact, they're moving in circles in 4 dimensions. But when these circles are projected down to 3-dimensional space, they become ellipses! This animation by Greg Egan shows the idea.
The plane here represents 2 of the 3 space dimensions we live in. The vertical direction is the mysterious fourth dimension. The planet goes around in a circle in 4-dimensional space. But down here in 3 dimensions, its 'shadow' moves in an ellipse!
What's this fourth dimension I'm talking about here? It's a lot like time. But it's not exactly time. It's the difference between ordinary time and another sort of time, which flows at a rate inversely proportional to the distance between the planet and the sun.
Egan's animation uses this other sort of time. Relative to this other time, the planet is moving at constant speed around a circle in 4 dimensions. But in ordinary time, its shadow in 3 dimensions moves faster when it's closer to the sun.
All this sounds crazy, but it's not some new physics theory. It's just a different way of thinking about Newtonian physics! Of course you can see that planets move in elliptical orbits without resorting to the 4th dimension. But it becomes a lot more obvious if you do!
Physicists have known about this viewpoint at least since 1980, thanks to a paper by the mathematical physicist Jürgen Moser. Some parts of the story are much older. A lot of papers have been written about it.
But I only realized how simple it is when I got a paper in my email from someone I didn't know: an amateur mathematician named Jesper Göransson. I get a lot of papers by crackpots, but the occasional gem like this makes up for all those.
The best thing about Göransson's 4-dimensional description of planetary motion is that it gives a clean explanation of an amazing fact. You can take any elliptical orbit, apply a rotation of 4-dimensional space, and get another valid orbit!
Of course we can rotate an elliptical orbit about the sun in the usual 3-dimensional way and get another elliptical orbit. The interesting part is that we can also do 4-dimensional rotations. This can make a round ellipse look skinny: when we tilt a circle into the fourth dimension, its 'shadow' in 3-dimensional space becomes thinner!
In fact, you can turn any elliptical orbit into any other elliptical orbit with the same energy by a 4-dimensional rotation of this sort. All elliptical orbits with the same energy are really just circular orbits on the same sphere in 4 dimensions!
For the details, try this:
I had to go through Göransson's calculations to convince myself that they were right. Here is his paper:

This image starts out as a dot. You keep zooming in to see more detail.
First it stretches out to become a line segment. As you zoom in further, you see its thickness. It's really a long thin rectangle.
But wait longer and you see it's really a field of dots. And zooming into any one of these dots, this process repeats... forever!
Each long thin rectangle is 10,000 times longer than the next smaller one.
So, you're looking at a very complicated set of points in the plane, whose dimension seems to depend on how closely you zoom in. In this example, created by Simon Willerton, the dimension keeps cycling:
But you can make examples that do other things.
The moral? Mathematicians have various ways of defining the dimension of a set of points in the plane, or even more general sets. A point, or a finite set of points, is 0-dimensional. A line, or a smooth curve, is 1-dimensional. A solid rectangle, or a disk, is 2-dimensional.
But sometimes it's more complicated! There are fractals whose dimension is not an integer... at least if we use the right definition of 'dimension'. The old Lebesgue dimension is always an integer, but the Hausdorff–Besicovich dimension or Minkowski dimension can be fractional, or even irrational.
And there are also sets whose dimension seems to depend on how closely you look at them! That's what we have here.
Willerton is working on a theory of scale-dependent dimension, to make this precise. He's writing a series of blog articles on it, and the first is here:
For the details, go here:
In 2007, NASA discovered seven very dark circles on a mountain in Mars. Using infrared cameras, they checked the temperature of these circles—and discovered that they didn't change much from day to night.
"They are cooler than the surrounding surface in the day and warmer at night," said Glen Cushing of the U.S. Geological Survey's Astrogeology Team. "Their thermal behavior is not as steady as large caves on Earth that often maintain a fairly constant temperature, but it is consistent with these being deep holes in the ground."
In short, they could be windows into caves!
They're called the Seven Sisters: Dena, Chloe, Wendy, Annie, Abby, Nikki and Jeanne. They range in diameter from about 100 to 250 meters.
They're on one of the highest places on Mars: a volcano named Arsia Mons near Mars' tallest mountain, Olympus Mons.
But the picture here is part of another story. A few years ago, an artist named Ron Guyatt started making "solar system travel posters." This was one of the first.
You can see them all here:
There are 3 pages of them. Click to make them bigger.
He says:
Space tourism is still a long ways off, but it's not hard to imagine that someday, tourists will visit the natural geological landmarks of other worlds much like they tour the Grand Canyon, Mount Everest or Ayers Rock. Each of these great tourist destinations needs a classic retro travel poster to entice visitors. Until the day people settle off-world and make their own destinations many of these may be the places that people will want to travel to. I hope that these posters can inspire people to think beyond our world to the limitless possibilities of the Universe.
I like this idea!
The posters on Guyatt's website are more abstract than the one here. Compare it to this:
Which do you like better? I like the less abstract version. But they're both good.
Puzzle: There are lots of things called "The Seven Sisters". Which ones do you know?
For some answers, look at the comments on my G+ post.
A petabyte is a lot of information. But how many petabytes does it take to completely describe one gram of water?
I'm running a workshop on Information and Entropy in early April, so I've got this sort of thing on my mind. The answer is: 500,000,000,000 terabytes. To see how to calculate this, and lots more, try:
The graphic here is originally from Mozy, but it was edited over at Gizmodo.
March 27, 2015
Puzzle: If the Earth became a black hole, how big would
this black hole be?
Answer: Its radius would be approximately 0.887 centimeters.
We can get quite far on this problem using just dimensional analysis. General relativity involves two constants: the gravitational constant \(G\) and the speed of light \(c\). \(G\) has units of force times distance2 per mass2, or $$ \frac{ML}{T^2} \times \frac{L^2}{M^2} = \frac{L^3}{T^2M} $$ \(c\) has units of length over time, so \(G/c^2\) has units of $$ \frac{T^2}{L^2} \times \frac{L^3}{T^2M} = \frac{L}{M} $$ Units of length per mass! So, to get the radius of a black hole, we just need to multiply its mass by \(G/c^2\). We'll get the right answer up to some constant factor.
We need to think harder to work out the constant factor, though Newtonian mechanics works just as well as general relativity for this: you can work out, for a given point mass, at what distance the escape velocity is the speed of light... and this just happens to be the exact radius of the event horizon of a black hole with that mass! It's just a nice coincidence.
So, the radius of a black hole of mass \(m\) — its so-called Schwarzschild radius — is $$ \frac{2Gm}{c^2} $$ Working this out in metric units, its radius in meters is \(1.4851 \times 10^{-27}\) times its mass in kilograms.
The mass of the Earth is \(5.972 \times 10^{24}\) kilograms. So, if you squashed the Earth down to a black hole, its Schwarzschild radius would be $$ 1.4851 \times 10^{-27}\; \frac{\mathrm{meters}}{\mathrm{kilogram}} \times \ 5.972 \times 10^{24}\; \mathrm{kilograms} = 0.008869 \ \mathrm{meters} $$ or about 0.887 centimeters.
Guess what: black holes are bigger on the inside — and they get bigger as they get older!
For example, take the big black hole in the center of our galaxy, called Sagittarius A*. It's about 2 million kilometers across. That's pretty big — but the orbit of Mercury is 60 times bigger. This black hole is old, roughly a billion years old. And here's the cool part: it's been growing on the inside all this time!
How is this possible? Well, since spacetime is severely warped in a black hole, its volume can be bigger than you'd guess from outside. And its volume can change. Since we understand general relativity quite well, we can calculate how this works! But nobody thought of doing it until last year, when Marios Christodoulou and my friend Carlo Rovelli did it.
How big is the black hole at the center of our galaxy? On the inside, it can hold a million solar systems! Its volume is about 1034 cubic kilometers! And it's growing at a rate of about 1025 cubic kilometers per year!
Or suppose you have an ordinary star that turns into a black hole. This black hole will last a long time before it evaporates due to Hawking radiation. Christodolou and Rovelli estimate how big its volume will get before this happens. And it gets really big — bigger than the current-day observable universe!
Before you get too excited, remember: people falling into the black hole will not have time to do anything fun inside. They will hit the singularity in a short time. Very very roughly speaking, the problem is not the shortage of space inside the black hole, it's the shortage of time.
If you fall into the black hole at the center of our galaxy, it will be about 1 minute, at most, before you hit the singularity. You will not get to see most of the space inside the black hole! The singularity is not in the 'middle' of the black hole - it's in your future. You will hit it before you can reach the 'middle'. So, you will only get to see part of the 'edge regions' inside the black hole.
The 'middle regions' can only be seen by people who fell in much earlier. And they can't see the 'edge', where you are!
And now for the serious part.
The hard part of this problem is defining the volume inside a black hole.
If you choose a moment in time, the black hole's event horizon at that moment is a sphere. There are infinitely many ways to extend this sphere to a solid ball. In other words: there are many ways to choose a slice of space inside the black hole whose boundary is your chosen sphere.
The slice can bend forwards in time, or backwards in time. We can choose a wiggly slice or a smooth one. Each slice has its own volume.
How do you choose one, so you can calculate its volume? Christodoulou and Rovelli choose the one with the largest volume. This may sound like it's cheating. But it's not.
Think of a simpler problem one dimension down. You have a loop of wire. You ask me: "What's the area of the surface whose boundary is this loop?"
I say: "That's a meaningless question! Which surface? There are lots!"
You say: "Pick the best one!"
So, it's up to me. I take some soapy water and make a soap film whose boundary is that loop. That's the surface I use. If the loop of wire is not too crazy in its shape, this surface is uniquely defined. In some sense it's the "least wiggly" surface I could choose.
This surface minimizes the area. A more wiggly surface would have more area.
Christodoulou and Rovelli are doing the same thing. But spacetime is different than space! If you choose a wiggly 3-dimensional spatial surface in spacetime, it will have less volume than a flatter surface with the same boundary!
So, the way to pick the flattest, nicest spatial surface inside our black hole is to pick the one that maximizes the volume.
If you tried to minimize the volume, you could get it as close to zero as you wanted. And this would have nothing to do with black holes! This would be true even in your living room.
Puzzle: why?
Here's the paper:
This computer is called JUQUEEN. You can see 7 big boxes here. Each box holds 4 racks. Each rack holds 16 boards. Each board holds 32 nodes. Each node has 32 cores.
A core is like the processor in your laptop. So, this computer is roughly like half a million laptops — all connected and working together. It can compute at a rate of 5 petaflops. That's 5,000,000,000,000,000 floating-point operations per second!
This computer was recently used to compute the ratio of the proton and neutron masses. A proton weighs about 1836 times as much as an electron. A neutron is a bit heavier: about 1839 times the electron mass.
This is important, since it means a lone proton is stable, while a lone neutron is not: in about 15 minutes, it will decay into a proton and some other stuff. This is why the universe is mainly made of hydrogen, not neutrons!
Why is the neutron a bit heavier? People have been wondering for a long time.
The answer lies in the Standard Model, our best theory of particles and all the forces except gravity. Protons and neutrons are made of quarks, and the Standard Model says exactly how this works. So, we can use the Standard Model to compute the ratio of proton and neutron masses.
But it's not easy! As anyone who has studied quantum field theory will tell you, this problem is a nightmare. For the course I took, in the final exam we had to compute how two electrons scatter off each other. I probably screwed up, because I only got a B+. But that problem is really, really easy compared to computing the mass of a proton or neutron.
The problem is that the strong force, which holds the quarks together, interacts with itself in a complicated way. The strong force is carried by particles called gluons. Quarks emit and absorb gluons. But gluons also emit and absorb gluons! So, a proton or neutron is like a blob containing 3 quarks - but a blob made of gluons, virtual quark-antiquark pairs, and some other virtual particles, all held together by their interactions.
To accurately compute the total energy of this blob, and thus its mass, you basically need to simulate it. And even though we know the basic rules, that takes a lot of computing.
But now it's been done!
You can see the world in a grain of sand... or even a single proton.
The abstract gives a tiny taste:
The existence and stability of atoms rely on the fact that neutrons are more massive than protons. The measured mass difference is only 0.14% of the average of the two masses. A slightly smaller or larger value would have led to a dramatically different universe. Here, we show that this difference results from the competition between electromagnetic and mass isospin breaking effects. We performed lattice quantum-chromodynamics and quantum-electrodynamics computations with four nondegenerate Wilson fermion flavors and computed the neutron-proton mass-splitting with an accuracy of 300 kilo.electron volts, which is greater than 0 by 5 standard deviations. We also determine the splittings in the Σ, Ξ, D, and Ξcc isospin multiplets, exceeding in some cases the precision of experimental measurements.
If you're a quantum field theory geek, you'll want to read the 'supplementary material', because that's where all the details are:
Here you'll see particle physics jargon blending with computing jargon in a marvelous symphony:
Starting with Sec. 6 we present the details of the many simulations that are performed and summarized here. The use of Rational Hybrid Monte-Carlo method is discussed with a special emphasis on the lowest eigenvalues of the Dirac operator. Autocorrelations are under control for our choice of parameters in the QCD part of our work. However, due to the zero mass of the photon and the correspondingly large correlation lengths, a standard Hybrid Monte-Carlo integration of the photon fields results in large autocorrelation times. We show how we solved this problem by developing a Fourier accelerated algorithm. For the propagator calculations we used a 2-level multi-grid approach to have several hundred source positions and significantly improve our statistics.
And here's a vastly harder challenge: do these calculations in a way where you can prove they are accurate up to some tolerance. We can't do this yet because we haven't even proved the Standard Model is mathematically consistent. Until we do, and until we develop a rigorous approach to computing things like the proton-neutron mass difference, there's always the danger that researchers are subconsciously choosing certain approximations because they seem to make the answer come out closer to what we observe.
Puzzle: Why are there just 7 big boxes here, not 8? Everything else comes in powers of 2. If it had 8 boxes, JUQUEEN would have
cores. But it has just 458752. Budget cuts?
For my April 2015 diary, go here.