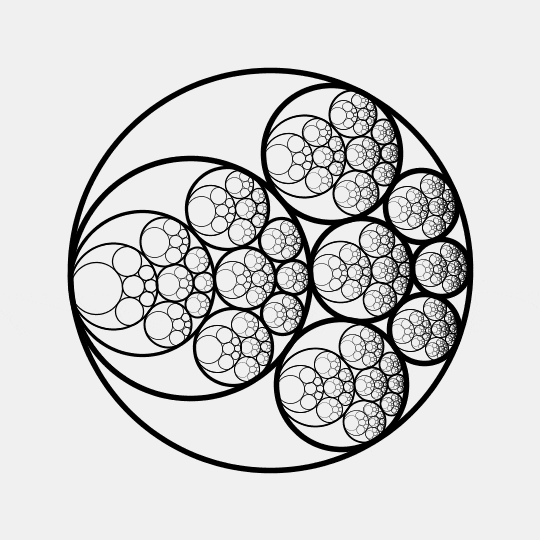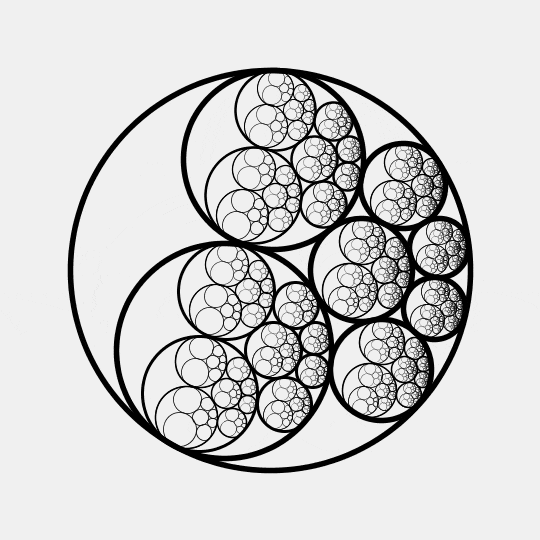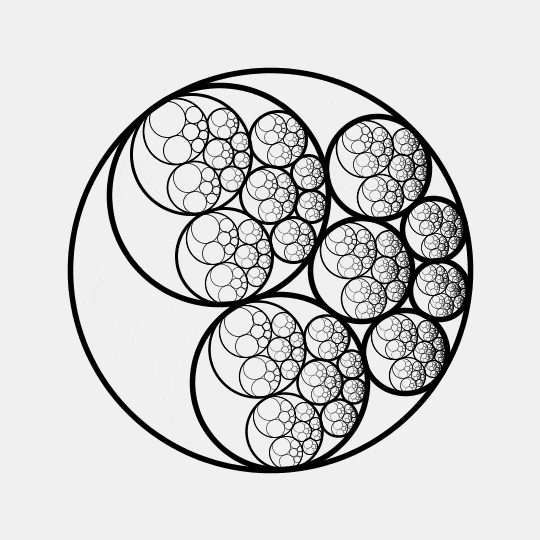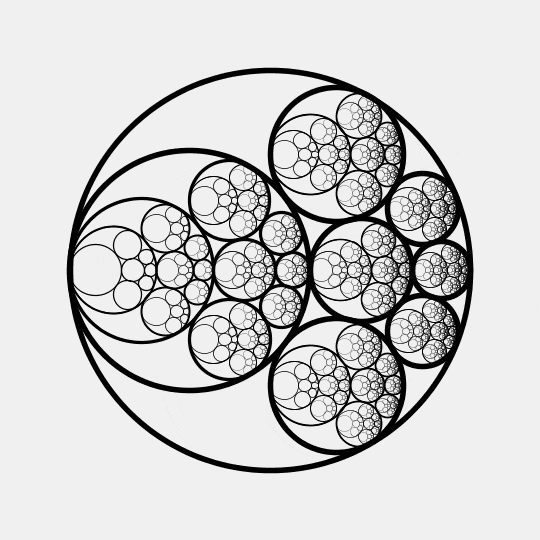
This beautiful animation by Gábor Damásdi illustrates an amazing result of Jakob Steiner. Namely: if you can snugly fit some circles inside one circle and outside another, you can move these circles around while they stay touching! They may need to change size, though.
Just for fun, this animation goes ahead and recursively uses the same pattern inside each of the smaller circles, ad infinitum.
This result by Steiner, proved in the 1800s, is usually called 'Steiner's porism'.
What the heck is a 'porism'?
This is one of those scary Greek math words like 'syzygy' and 'plethysm' — words that nobody ever seems to explain in a clear, intuitive way. It's not promising that the Wikipedia entry for 'porism' begins:
The subject of porisms is perplexed by the multitude of different views which have been held by geometers as to what a porism really was and is.In brief, a porism is something in between a problem and a theorem. Here's what Wikipedia says:
The older geometers regarded a theorem as directed to proving what is proposed, a problem as directed to constructing what is proposed, and finally a porism as directed to finding what is proposed.
Got it?
Gábor Damásdi has a fun page on Tumblr:
He writes:
Hi there!I am a Hungarian math student, currently doing my master degree at Eötvös Loránd University in Budapest. In my free time I like to draw mathematical stuff like fractals, tillings, tessellations, polyhedrons and so on.
I usually use the following programs to create them: Processing, Geogebra, Gimp, Inksckape. If you want to do similar pictures this is a good place to start: processing.org.
I also organize math camps and math competitions in Hungary. I usually work with a really good foundation called the "The joy of thinking foundation".If you are interested you can find more information here: http://agondolkodasorome.hu/en/.
Jakob Steiner did a lot of fundamental work in projective geometry in the 1800s. A contemporary described him this:
He is a middle-aged man, of pretty stout proportions, has a long intellectual face, with beard and moustache and a fine prominent forehead, hair dark rather inclining to turn grey. The first thing that strikes you on his face is a dash of care and anxiety, almost pain, as if arising from physical suffering - he has rheumatism. He never prepares his lectures beforehand. He thus often stumbles or fails to prove what he wishes at the moment, and at every such failure he is sure to make some characteristic remark.
Here is some information about his porism:

It captures the quaintness of some older Hong Kong shops as well as the charm of the cat. A lot of older neighborhoods are getting displaced by fancy skyscrapers, but Lisa and I spent a lot of time in Ya Mau Tei, an area which retains its charm. That's where Lisa visits the jade market. And that's where I saw this cat in a store window, sleeping next to a statue of a cat:

We also visited a lot of temples. Here is Lisa in the Nan Lian Garden, near a Buddhist nunnery:

and here's another view of that garden:

Set theory starts out as a very simple way of organizing our thoughtsb something every student should learn. But it gets more tricky when we start pondering infinite sets. And when we start pondering the universe — the collection of all sets — it gets a lot harder. Mathematicians have learned that there are obstacles to fully understanding the universe.
The collection of all sets can't be a set — Bertrand Russell and other logicians discovered this over a century ago. But more importantly, Gödel's theorem puts limits on how well any axioms can pin down the properties of the universe. Most mathematicians like to use the Zermelo-Fraenkel axioms together with the axiom of choice. But there are many questions left unsettled by these axioms.
Knowing this, you might give up on trying to fully understand the universe. That's actually what most mathematicians do. Frankly, the questions left unsettled by the ZFC axioms don't seem very urgent to most of us!
But set theorists don't give up. They've developed a lot of fascinating ways to make progress despite the obstacles.
In the 1960s, Paul Cohen introduced forcing. This is a way to make the universe larger, by making up a bunch of new sets, without violating the axioms you're using.
If I think the universe is \(U\), you can use forcing to say "fine, but it's equally consistent to assume the universe is some larger collection \(V\)". Cohen used this to show the axiom of choice couldn't be proved from the other axioms in ZFC. Given a universe U where the Zermelo-Fraenkel axioms hold, he used forcing to build a bigger universe \(V\) where those axioms still hold, but the axiom of choice does not!
As an undergrad, I gave up my studies of set theory before I learned forcing. It was too hard to understand, and probably too badly explained: I don't think anyone even said what I just told you! I moved on to other things - there's a lot of fun stuff to learn. But for modern set theorists, forcing is utterly basic.
So what's new?
One new thing is 'set-theoretic geology':
So, starting with some universe \(V\), we look for a smaller universe \(U\) that can give rise to \(V\) by forcing. If this is true, we call \(U\) a ground for \(V\).
There can be lots of grounds for a universe \(V\). This raises a big question: if we have two grounds for \(V\), is there a ground that's contained in both?
In 2015, Toshimichi Usuba showed this is true! In fact he showed that for any set of grounds of \(V\), there's a ground contained in all of these.
This raises another big question: is there a smallest ground, a ground contained in all other grounds? If so, this is called the bedrock of our universe \(V\).
Usuba showed that the bedrock exists if a certain kind of infinite number exists! There are different sizes of infinity, and this particular kind is called 'hyper-huge'. It's so huge that it's not even explained in the Wikipedia article on huge cardinals. So, I can't explain it to you, or even to myself.
But still, I think I get the basic idea: if we have a large enough infinity, digging down infinitely far that much will get us down to the bedrock of the universe.
Naively, I tend to favor small universes. So, the bedrock appeals to me. However, you need a big universe to have large infinities like 'hyper-huge cardinals'. So, my minimalist philosophy runs into a problem, because your universe needs to contain big infinities for you to 'have time' to dig deep enough to hit bedrock!
Is this a paradox? Certainly not in the literal sense of a logical contradiction. But how about in the sense of something bizarre that makes no sense?
Probably not. There's a way to take the universe and divide into 'levels', called the von Neumann hierarchy. If you assert the existence of large cardinals, you're making the universe 'taller' — you're adding extra levels. But if you stick in extra sets by forcing, you might be making the universe 'wider' — that is, adding more sets at existing levels. So, you may need a super-huge cardinal to have enough time to chip away at the stuff in all these levels until you hit bedrock.
This is just my guess; I'm no expert. For more information from an actual expert try Joel David Hamkins' article.
He talks about a concept called the 'mantle', without explaining it. But he explains it in a comment to his post: the mantle of the universe is the intersection of all grounds. If there's a hyper-huge cardinal, this must be the bedrock. If not, other things can happen.