
ANITA, the Antarctic Impulse Transient Antenna, detects ultra-high-energy cosmic neutrinos. Here it is in front of Mount Erebus.
It's seen some amazing things... possibly signs of physics beyond the Standard Model! But first let me say a word about how it works.
A neutrino shooting through Antarctic ice hits an atom and creates a shower of charged particles moving faster than the speed of light in ice. They create Cherenkov radiation, the electromagnetic analogue of a sonic boom. Some of this radiation is in the form of radio waves. As they leave the ice, these waves refract. It's called the Askaryan effect.
ANITA, hanging from a floating weather balloon, has seen many events like this. But two of these pulses came up through the Earth's crust, which is not how it's supposed to work!
An ultra-high-energy neutrino shouldn't be able to go through the Earth. Low-energy neutrinos can go through light years of rock, but their rate of absorption goes up with their energy. The pulses seen by ANITA seem to have come from particles with an energy of about \(0.6\) EeV: that is, \(6 \cdot 10^{17}\) electron volts. That's an extremely high energy. Such energetic neutrinos should not be able to penetrate lots of rock.
This picture explains it: "cross section" is, roughly speaking, proportional to the absorption probability.
ANITA saw one of these events in 2006, and one in 2014. Another Antarctic neutrino detector, IceCube, has seen similar strange events.
So, something strange is going on. This could be great! But don't believe the theories yet — it's way too early.
For more, read:
More progress on a famous problem!
A subset of the plane has "diameter 1" if the distance between any two points in this set is ≤ 1. For example, an equilateral triangle with edges of length 1 has diameter 1... and it doesn't fit in the circle with diameter 1.

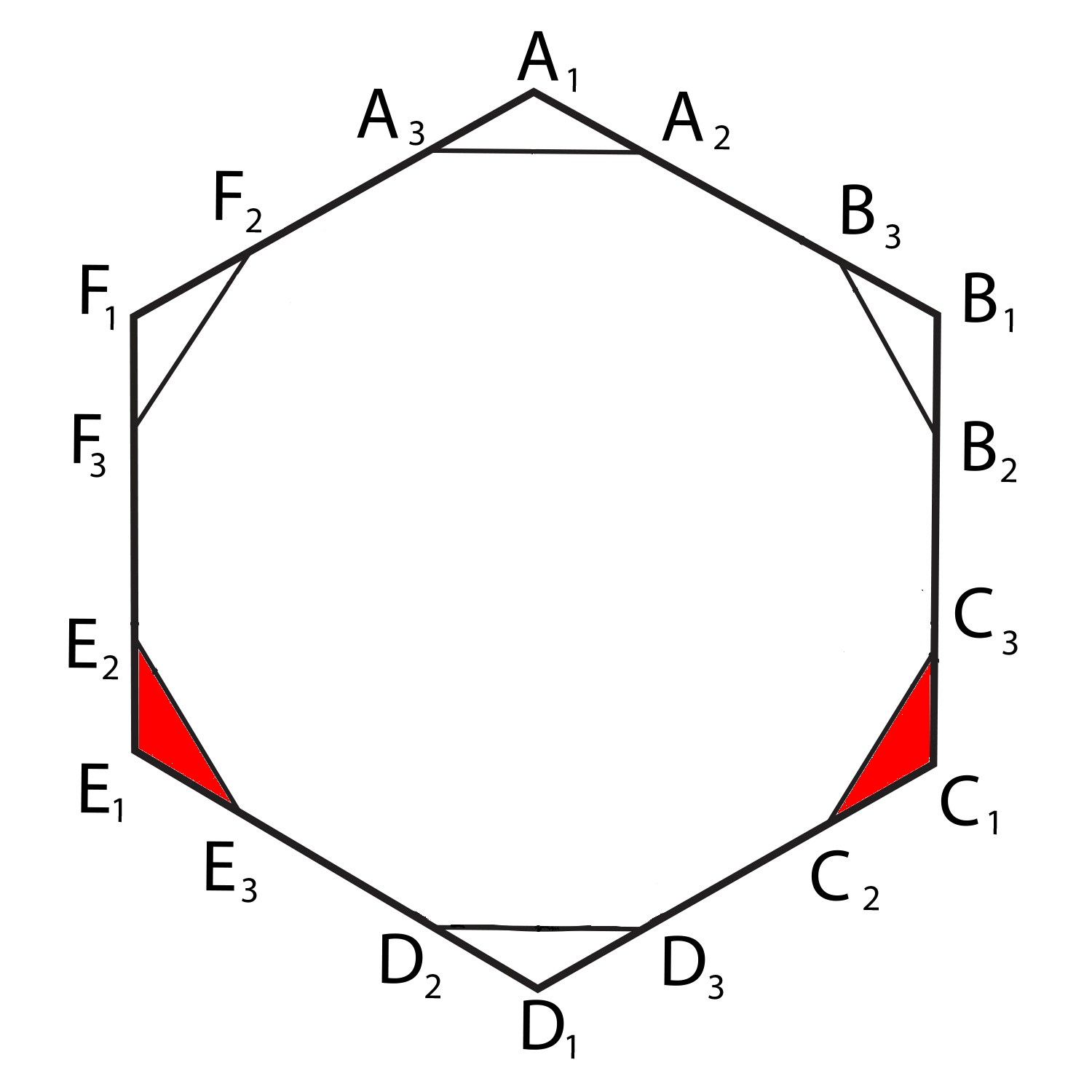
In 1914 the famous mathematician Lebesgue sent a letter to his pal Pál. He challenged Pál to find the convex set with least possible area such that every set of diameter 1 fits inside... at least after you rotate, translate and/or reflect it.

Pál showed the smallest regular hexagon containing a disk of diameter 1 would work. Its area is
But he also showed you could cut off two corners, and get a solution of area just
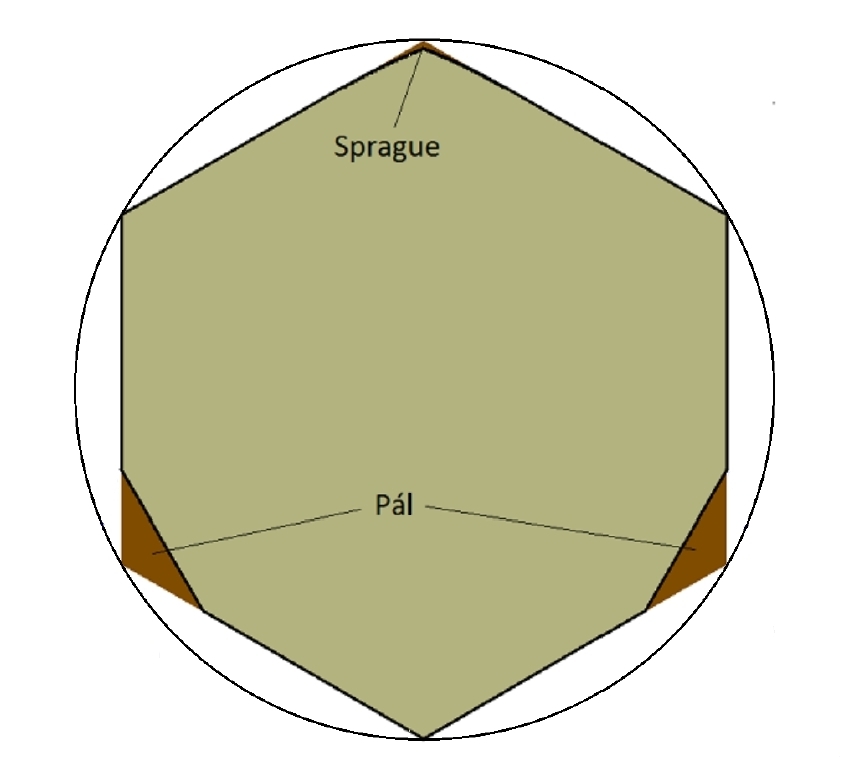
In 1936, Sprague showed another piece of the hexagon could be removed and still leave a universal covering.
This piece has area about 0.02. Cutting it out, we get a universal covering of area
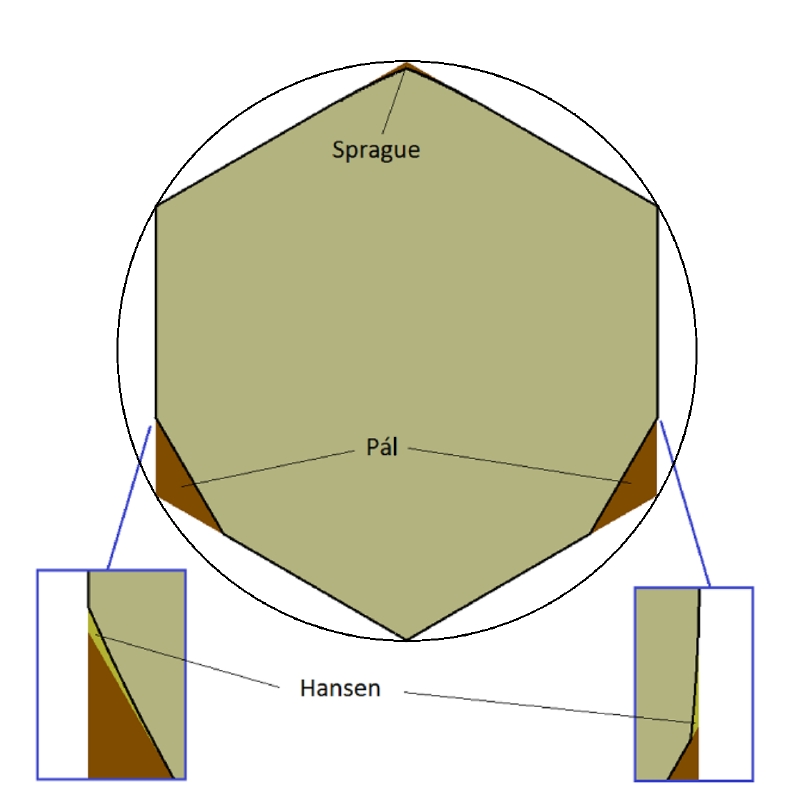
In 1992, Hansen removed two microscopic slivers from Sprague's universal covering and got an even better one!
These slivers were absurdly small, with areas of roughly \(4 \cdot 10^{-11}\) and \(8 \cdot 10^{-21}\). He got a universal covering of area
At this point two mathematicians joked:
"...it does seem safe to guess that progress on this problem, which has been painfully slow in the past, may be even more painfully slow in the future."But that's when Philip Gibbs came in!
He found a way to remove a piece about a million times bigger than Hansen’s larger sliver. Its area was a whopping \(2 \cdot 10^{-5}\), leaving a universal covering of area
I met Philip Gibbs in London last week at a workshop on Noether's theorem. It turned out he's now done even better! He has chopped off another enormous chunk, with area \( 2 \cdot 10^{-5}\), leaving a universal covering of area just
Huge progress! For details, read his paper:
The moral is that even plane geometry holds deep problems connected to optimization.
Lebesgue's universal covering problem, the sofa moving problem, the Moser worm problem, Bellman's lost-in-a-forest problem — we just don't know powerful techniques to tackle these... yet.

For more on Lebesgue's univeral covering problem, read these:

A polygon can be dissected into straight-edged pieces which you can rearrange to get any other polygon of the same area! This is called the Wallace–Bolyai–Gerwien theorem.
In fact, you can always use a "hinged" dissection, as illustrated here by Rodrigo Silveira Camaro:
This was proved in 2007:
But what about higher dimensions? Two polyhedra are "scissors-congruent" if you can cut one into finitely many polyhedral pieces, then reassemble them to get the other. In 1900 Hilbert asked: are any two polyhedra with the same area scissors-congruent? His student Max Dehn answered this in less than a year: no!
The cube, and a regular tetahedron with the same volume, are not scissors-congruent. To prove this Dehn found another invariant of scissors-congruence beside the volume!
But this is just the beginning of the story, which now involves hyperbolic space, algebraic K-theory, and even ideas connected to quantum gravity, like the famous "pentagon identity" arising from two ways to chop this shape into tetrahedra:

For more:
The population of insects has been crashing worldwide. Butterflies and moths are down 35% in the last 40 years. Other invertebrates are down even more:
Here we see the milligrams of arthropods (like insects) caught in sticky traps on the ground (A) and forest canopy (B) in a rain forest in Puerto Rico. Dramatic collapse! And it hurts the whole ecosystem: lizard populations are halved or worse. For more details, read the actual study:

New progress on a hard problem: Greg Egan broke the record for the shortest number with the digits 1 through 7 arranged in all possible orders. He found one with just 5908 digits.
Here is Egan's solution. It's 4 digits shorter than the previous best, and he got it using ideas from Aaron Williams' work on Hamiltonian cycles on Cayley graphs:

But what's the pattern? What's really going on?
Robin Houston noticed that the new winner containing all permutations of \(n=7\) digits has $$ n! + (n-1)! + (n-2)! + (n-3)! + (n-3) = 5908 $$ digits. And Egan also found new winners for \(n=8\) and \(n = 9\) which also fit this pattern!
However, this formula does not correctly predict the length of the winners for \(n=3\) and \(n=4\)... so the true pattern is more complicated.
After I wrote the above on Twitter, progress continued, with some surprising twists. I persuaded Erica Klarreich to write an article about the story, so go here for the rest:
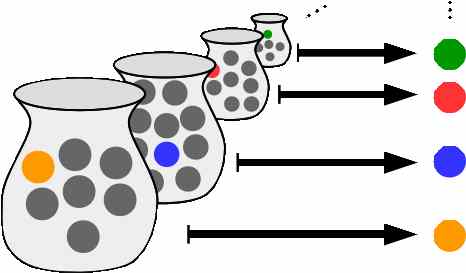
The axiom of choice says that given any collection of bins, each containing at least one object, it is possible to make a selection of exactly one object from each bin, even if the collection is infinite. It has shocking consequences... but so does its negation!
The axiom of choice implies that we can't define lengths, areas, and volumes for all sets in a way that obeys a short list of reasonable-sounding rules. Indeed, we can chop a ball into 5 subsets and rearrange them to get 2 balls: the "Banach-Tarski paradox".
If we assume the negation of the axiom of choice, we can make this problem go away. Technically: Solovay found models of ZF¬C (set theory and the negation of axiom of choice) where all subsets of Euclidean space are measurable! But that doesn't mean life is trouble-free.

Indeed, in all known models of ZF¬C, there is a set that can be partitioned into strictly more equivalence classes than the original set has elements! (More precisely, there's no injection from the set of equivalence classes to the original set.) It's hard to find axioms that give just what we want, and nothing freaky.

Today I learned: unlike in our universe, in 2d space solids melt in two separate stages! Solid, hexatic, liquid — as shown above.
This has been discussed by theoretical physicists since the 1970s, but in 2013 it was confirmed experimentally using a layer of small magnetized beads. They saw two phase transitions as we shake these beads harder and harder, shifting them from a solid phase to a liquid!
The solid phase has long-range correlations between the orientation of the rows of beads: that's what 'long range orientational order' means. The actual positions of the beads are also correlated, but these correlations decay according to a power law that's what 'quasi-long range translational order' means.
In the hexatic phase, the orientational correlations decay with distance following a power law!
In the liquid phase, they decay exponentially.
In 3d, crystals can have long-range translational order. In the 1960s, Mermin and Wagner proved this is impossible in 2d if the particle only interact with short-range forces. In the 1970s, Kosterlitz, Thouless, Halperin, Nelson and Young worked out how solids melt in 2d, and discovered that there should be a hexatic phase between solid and liquid.
For details, see: