Einstein's Equation

To state Einstein's equation in simple English, we need to consider a round ball of test particles that are all initially at rest relative to each other. As we have seen, this is a sensible notion only in the limit where the ball is very small. If we start with such a ball of particles, it will, to second order in time, become an ellipsoid as time passes. This should not be too surprising, because any linear transformation applied to a ball gives an ellipsoid, and as the saying goes, ``everything is linear to first order''. Here we get a bit more: the relative velocity of the particles starts out being zero, so to first order in time the ball does not change shape at all: the change is a second-order effect.

Let $V(t)$ be the volume of the ball after a proper time $t$ has elapsed, as measured by the particle at the center of the ball. Then Einstein's equation says:

$${\ddot V\over V} \Bigr\vert _{t = 0} = -{1\over 2} \left( \b... ...m -momentum \; in \;} z {\rm\; direction} \end{array} \right)$$

where these flows are measured at the center of the ball at time zero, using local inertial coordinates. These flows are the diagonal components of a $4 \times 4$ matrix $T$ called the `stress-energy tensor'. The components $T_{\alpha \beta}$ of this matrix say how much momentum in the $\alpha$ direction is flowing in the $\beta$ direction through a given point of spacetime, where $\alpha,\beta = t,x,y,z$. The flow of $t$-momentum in the $t$-direction is just the energy density, often denoted $\rho$. The flow of $x$-momentum in the $x$-direction is the `pressure in the $x$ direction' denoted $P_x$, and similarly for $y$ and $z$. It takes a while to figure out why pressure is really the flow of momentum, but it is eminently worth doing. Most texts explain this fact by considering the example of an ideal gas.

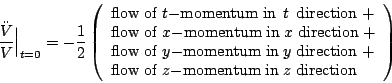
In any event, we may summarize Einstein's equation as follows:

$${\ddot V\over V} \Bigr\vert _{t = 0} = -{1\over 2} (\rho + P_x + P_y + P_z).$$ (2)

This equation says that positive energy density and positive pressure curve spacetime in a way that makes a freely falling ball of point particles tend to shrink. Since $E = mc^2$ and we are working in units where $c = 1$, ordinary mass density counts as a form of energy density. Thus a massive object will make a swarm of freely falling particles at rest around it start to shrink. In short: gravity attracts.

We promised to state Einstein's equation in plain English, but have not done so yet. Here it is:

Given a small ball of freely falling test particles initially at rest with respect to each other, the rate at which it begins to shrink is proportional to its volume times: the energy density at the center of the ball, plus the pressure in the $x$ direction at that point, plus the pressure in the $y$ direction, plus the pressure in the $z$ direction.

In the final section of this article, we will prove that this sentence is equivalent to Einstein's equation. The reader who already knows general relativity may be somewhat skeptical of this claim. After all, Einstein's equation in its usual tensorial form is really a bunch of equations: the left and right sides of equation (1) are $4 \times 4$ matrices. It is hard to believe that the single equation (2) captures all that information. It does, though, as long as we include one bit of fine print: in order to get the full content of the Einstein equation from equation (2), we must consider small balls with all possible initial velocities -- i.e., balls that begin at rest in all possible local inertial reference frames.

Before we begin, it is worth noting an even simpler formulation of Einstein's equation that applies when the pressure is the same in every direction:

Given a small ball of freely falling test particles initially at rest with respect to each other, the rate at which it begins to shrink is proportional to its volume times: the energy density at the center of the ball plus three times the pressure at that point.

This version is only sufficient for `isotropic' situations: that is, those in which all directions look the same in some local inertial reference frame. But, since the simplest models of cosmology treat the universe as isotropic -- at least approximately, on large enough distance scales -- this is all we shall need to derive an equation describing the big bang!

© 2006 John Baez and Emory Bunn

home