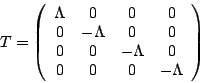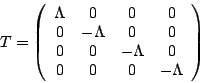Next: Spatial Curvature
Up: Some Consequences
Previous: The Big Bang
The simplified big bang model just described is inaccurate for
the very early history of the universe, when the pressure of radiation
was important. Moreover, recent observations seem to indicate that it is
seriously inaccurate even in the present epoch. First of all, it seems
that much of the energy density is not accounted for by known forms of
matter. Still more shocking, it seems that the expansion of the
universe may be accelerating rather than slowing down! One possibility
is that the energy density and pressure are nonzero even for the vacuum.
For the vacuum to not pick out a preferred notion of `rest', its
stress-energy tensor must be proportional to the metric. In local
inertial coordinates this means that the stress-energy tensor
of the vacuum must be
where 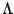 is called the `cosmological
constant'. This amounts to giving empty space an energy density equal
to
is called the `cosmological
constant'. This amounts to giving empty space an energy density equal
to 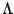 and pressure equal to
and pressure equal to 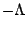 , so that
, so that 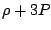 for
the vacuum is
for
the vacuum is 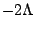 . Here pressure effects dominate because there are
more dimensions of space than of time! If we add this cosmological
constant term to equation (3), we get
. Here pressure effects dominate because there are
more dimensions of space than of time! If we add this cosmological
constant term to equation (3), we get
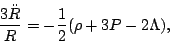 |
(4) |
where 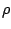 and
and 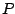 are the energy density and pressure due to matter.
If we treat matter as we did before, this gives
are the energy density and pressure due to matter.
If we treat matter as we did before, this gives
Thus, once the universe expands sufficiently, the cosmological constant
becomes more important than the energy density of matter in
determining the fate of the universe. If 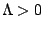 ,
a roughly exponential expansion will then ensue. This seems
to be happening in our universe now.
,
a roughly exponential expansion will then ensue. This seems
to be happening in our universe now.
Next: Spatial Curvature
Up: Some Consequences
Previous: The Big Bang
© 2006 John Baez and Emory Bunn