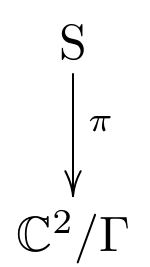
that's one-to-one away from the singularity. There are many resolutions, but one minimal resolution. All others factor uniquely through this one:
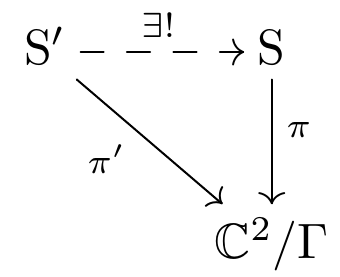

that's one-to-one away from the singularity. There are many resolutions, but one minimal resolution. All others factor uniquely through this one:
