• The cyclic groups, ℤ/n 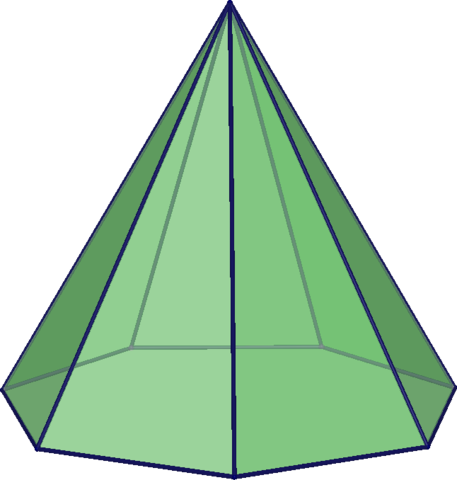
• The dihedral groups, Dn 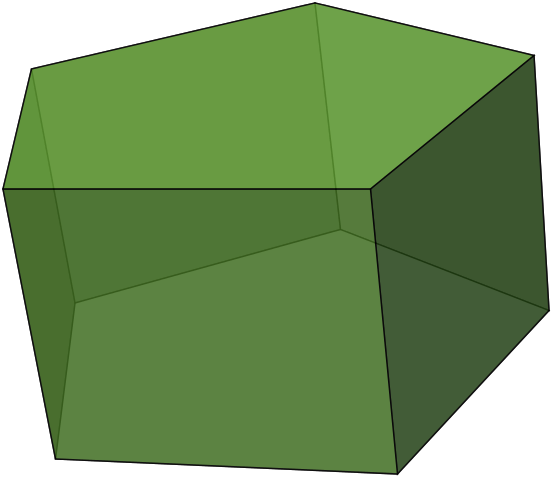
• The symmetry group of the tetrahedron, A4 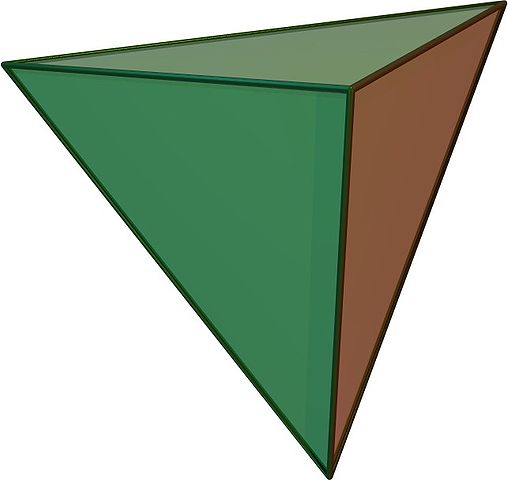
• The symmetry group of the cube or octahedron, S4 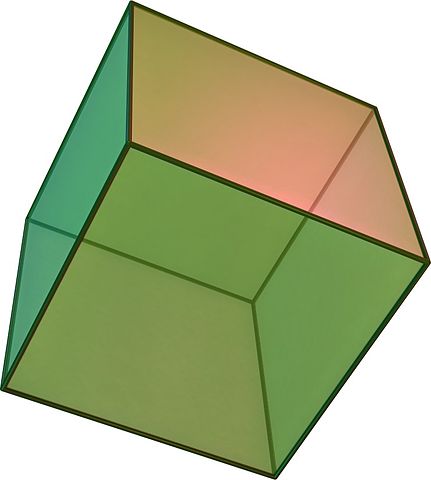
• The symmetry group of the dodecahedron or icosahedron, A5 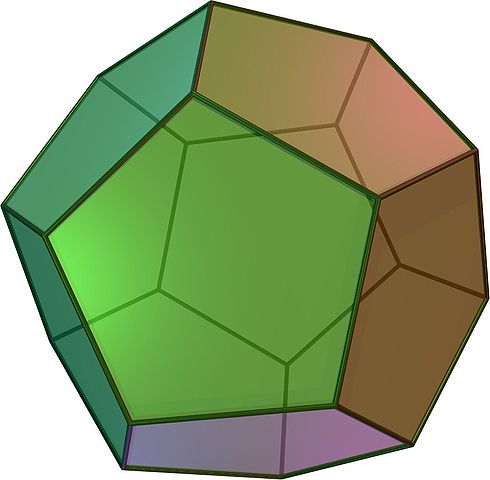
• The cyclic groups, ℤ/n 
• The dihedral groups, Dn 
• The symmetry group of the tetrahedron, A4 
• The symmetry group of the cube or octahedron, S4 
• The symmetry group of the dodecahedron or icosahedron, A5 