- ... ball.1
- If you want to be really concrete, imagine a spinning gyroscope
fitting snugly in a box. Rotate the box.
- ... (frames).2
- In other words, a element of
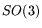 determines a mapping of
determines a mapping of 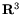 to
to 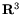 . As it happens,
the action is faithful, i.e., the mapping determines the element of
. As it happens,
the action is faithful, i.e., the mapping determines the element of
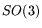 .
.
- ... moment.3
- A quick review: write
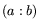 for the equivalence
class of
for the equivalence
class of 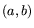 . We will associate either a complex number
. We will associate either a complex number 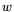 or else
or else 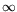 with each class
with each class 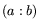 . If
. If 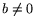 , then
, then
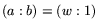 , where
, where 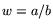 . All pairs of the form
. All pairs of the form 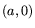 belong to the
class
belong to the
class 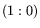 . So we associate
. So we associate 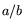 with
with 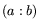 if
if 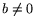 , and
, and
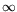 with
with 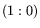 . Mapping the complex plane plus
. Mapping the complex plane plus 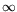 to the
Riemann sphere via the usual stereographic projection completes the trick.
Some sample points to bear in mind: the north pole is
to the
Riemann sphere via the usual stereographic projection completes the trick.
Some sample points to bear in mind: the north pole is 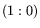 ; the south
pole is
; the south
pole is 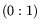 ; points on the equator have the form
; points on the equator have the form
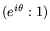 .
(For the purist, the special treatment of
.
(For the purist, the special treatment of 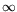 rankles. It is not
singled out on either the complex projective line or on the Riemann sphere.
Later I will show how to set up the correspondence without this blemish.)
rankles. It is not
singled out on either the complex projective line or on the Riemann sphere.
Later I will show how to set up the correspondence without this blemish.)
- ... simple4
- In
the infinite dimensional case, you have to use the spectral decomposition
of
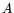 instead of an orthonormal basis of eigenvectors; another reason why
spin is simpler than position.
instead of an orthonormal basis of eigenvectors; another reason why
spin is simpler than position.
-
... proportional
to
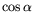 .
5
.
5
- Why wouldn't the electron simply snap into
alignment with the magnetic field? Answer: the spinning electron would act
like a gyroscope, and precess in response to the torque exerted by the
field. Thus it would maintain its angle of inclination to the field.