_guest post by **[Jade Master](https://sites.google.com/view/jadeedenstarmaster/home)**_
I just finished a [paper](https://arxiv.org/abs/1904.09091) which uses Lawvere theories to generalize Petri nets. I can think of two reasons why people might be interested in this:
* Category theorists love Lawvere theories and are in awe of their power. However, it can be hard to find instances where Lawvere theories are used to get something specific and practical accomplished.
* There are lots of papers on Petri nets and their variants. The bibliography on [Petri nets world](http://www.informatik.uni-hamburg.de/TGI/PetriNets/bibliographies/aboutpnbibl.html) has over 8500 citations. This generalization puts some of the more popular variants under a common framework and allows for exploration of the relationships between them.
This is a blog for category theory so I figured I'd tell you what a Petri net is.
**Definition:** A **Petri net** is a pair of functions
$$ (s,t \colon T \to \mathbb{N}[S]) $$
where $\mathbb{N} \colon \mathsf{Set} \to \mathsf{Set}$ is the free commutative monoid monad which sends a set to (the underlying set of) the free commutative monoid on that set. A Petri net can be thought of as a graph whose vertices are elements of a free commutative monoid. $T$ is called the set of **transitions**, $S$ is the set of **places**, and $s$ and $t$ are the **source** and **target** functions. The idea is that each place can hold a natural number of tokens which can be shuffled around by a transition in proportions given by its source and target.
There is a classical result which says that every Lawvere theory $\mathsf{Q}$ gives a monad $M_{\mathsf{Q}} \colon \mathsf{Set} \to \mathsf{Set}$. This generalizes the monad $\mathbb{N}$. We use this to generalize Petri nets into $\mathsf{Q}$-nets.
**Definition** A $\mathsf{Q}$-net $P$ is a pair of functions
$$ (s,t \colon T \to M_{\mathsf{Q}} S) $$
A morphism from $P$ to a $\mathsf{Q}$-net
$$ (P' = s',t' \colon T' \to M_{\mathsf{Q}} S')$$
is a pair of functions $ f\colon T \to T',g \colon S \to S'$ that respect the source and target functions of $P$ and $P'$. This defines a category $\mathsf{Q}$-net.
This category depends functorially on the Lawvere theory $\mathbf{Q}$. Indeed there is a functor
$$(-)\text{-}\mathsf{Net} \colon \mathsf{Law} \to \mathsf{Cat}$$
A classical result says that morphisms of Lawvere theories give nice morphisms of the monads they induce. This relationship is used to define the functors in the image of $(-)$-$\mathsf{Net}$.
Functoriality is nice. We have the following diagram of Lawvere theories:
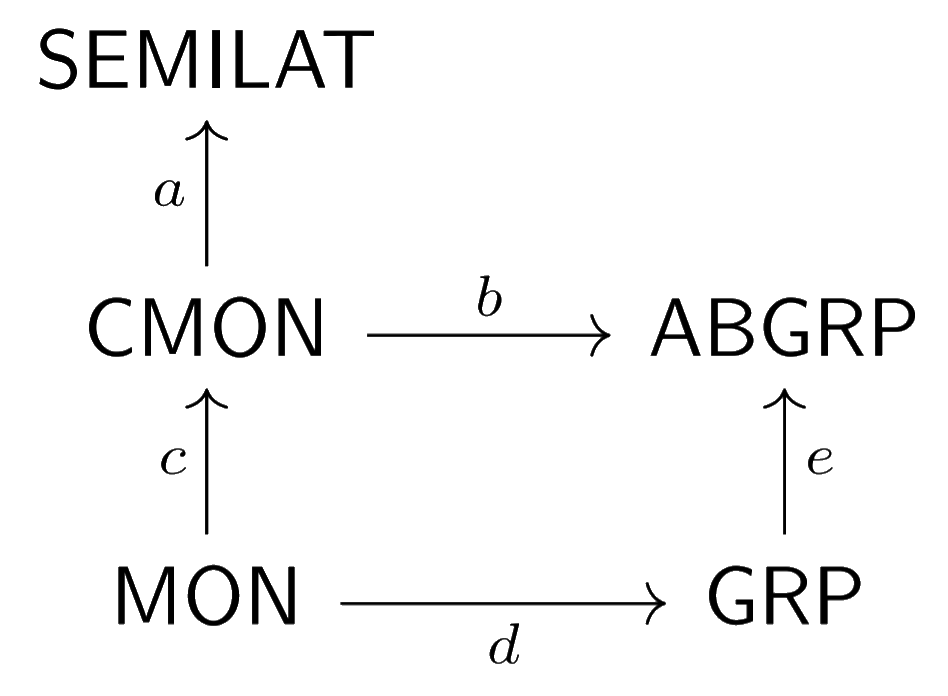 where
* $\mathsf{SEMILAT}$ is the Lawvere theory of semi-lattices i.e. idempotent commutative monoids,
* $\mathsf{CMON}$ is the Lawvere theory of commutative monoids,
* $\mathsf{MON}$ is the Lawvere theory of monoids,
* $\mathsf{ABGRP}$ is the Lawvere theory of abelian groups and,
* $\mathsf{GRP}$ is the Lawvere theory of groups.
I won't say what the functors in this diagram are except that they are the most natural functors of their type; I refer you to my paper to see what they actually are. This diagram induces the following diagram of categories using the functor $(-)$-$\mathsf{Net}$:
where
* $\mathsf{SEMILAT}$ is the Lawvere theory of semi-lattices i.e. idempotent commutative monoids,
* $\mathsf{CMON}$ is the Lawvere theory of commutative monoids,
* $\mathsf{MON}$ is the Lawvere theory of monoids,
* $\mathsf{ABGRP}$ is the Lawvere theory of abelian groups and,
* $\mathsf{GRP}$ is the Lawvere theory of groups.
I won't say what the functors in this diagram are except that they are the most natural functors of their type; I refer you to my paper to see what they actually are. This diagram induces the following diagram of categories using the functor $(-)$-$\mathsf{Net}$:
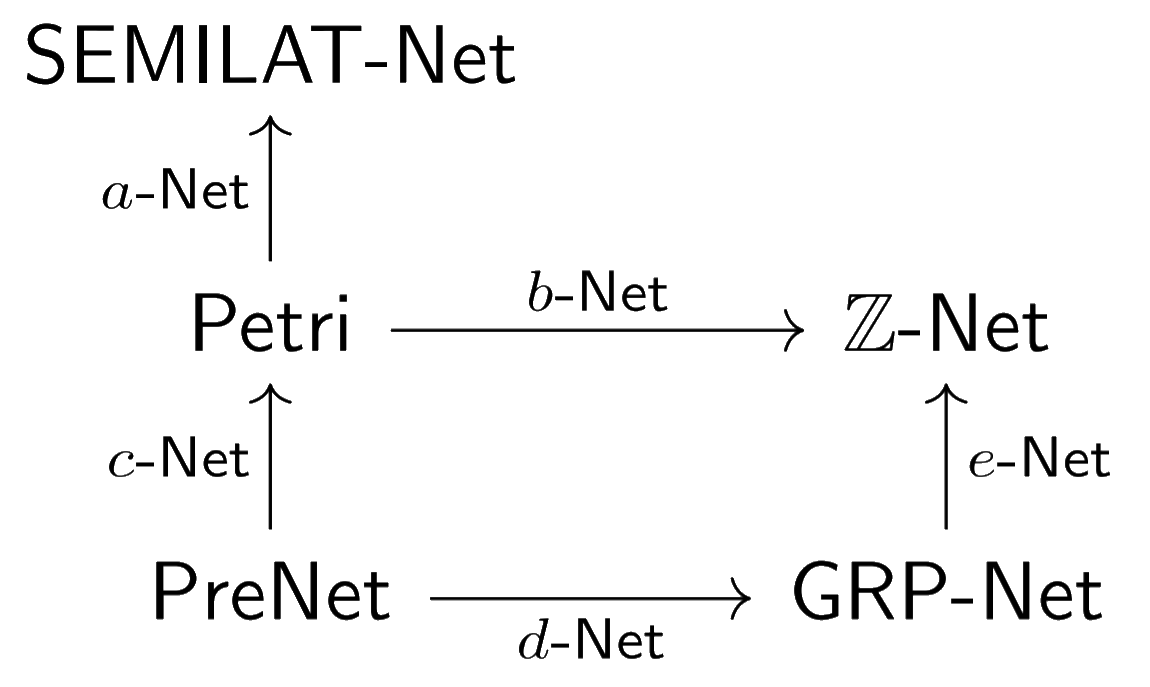 Many of the categories here are familiar to the Petri net community.
* $\mathsf{SEMILAT}$-$\mathsf{Net}$ is the category of elementary net systems. These are Petri nets which can have a maximum of one token in each place. Elementary net systems are used to represent non-concurrent programs; the location of the token represents how far along the computer is in execution.
* $\mathsf{Petri}$ is the good old category of Petri nets.
* $\mathsf{PreNet}$ is the category of pre-nets; Petri nets which are equipped with an ordering of the places on their input and output. These are useful for keeping track of causality in sequences of processes.
* $\mathbb{Z}$-$\mathsf{Net}$ is the category of [integer nets](https://arxiv.org/abs/1805.05988). These are [lending Petri nets](https://www.sciencedirect.com/science/article/pii/S0167642315001021) without a few properties. Integer nets and lending Petri nets are useful for modeling credit and borrowing. Places can hold negative tokens which represent debt.
Some of the functors in this diagram are known. $c$-$\mathsf{Net}$ and $e$-$\mathsf{Net}$ are commonly referred to as **abelianization**. This is because the $c$-$\mathsf{Net}$ sends a pre-net to the Petri net with an abelianized free monoid of places by forgetting about the ordering on the input and output of each species. $e$-$\mathsf{Net}$ is an analogous functor for $\mathbb{Z}$-$\mathsf{Net}$ and their non-commutative cousin $\mathsf{GRP}$-$\mathsf{Net}$.
This all sounds great but definitions are cheap. To justify a generalization can show that in its examples familiar consequences follow. Petri nets present free commutative monoidal categories: i.e., there is a meaningful adjunction between the category of Petri nets and a category where the objects are commutative monoidal categories. Commutative monoidal categories are symmetric monoidal categories whose symmetries are given by the identity. If you prefer, you can think of commutative monoidal categories categories as commutative monoid objects in $\mathsf{Cat}$.
This statement can be seen as a justification of the usefulness of Petri nets, because symmetric monoidal categories are the language of processes which can be done in sequence and in parallel. This adjunction makes precise the way in which Petri nets represent processes and gives a mathematical description of the way transitions shuffle tokens around in a Petri net. For a Petri net $P$, the free commutative monoidal category on $P$ is a category where the objects are all possible token configurations and the morphisms are all possible processes which bring one token configuration to another.
If the definition of $\mathsf{Q}$-$\mathsf{Net}$ is any good we should have a similar statement for $\mathsf{Q}$-nets. Indeed, $\mathsf{Q}$-nets present free models of $\mathsf{Q}$ in $\mathsf{Cat}$. There is an adjunction
$$F_{\mathsf{Q}} \dashv U_{\mathsf{Q}} \colon\mathsf{Q}\text{-}\mathsf{Net} \to \mathsf{Q}\text{-}\mathsf{Cat}$$
where $\mathsf{Q}$-$\mathsf{Cat}$ is the subcategory of $\mathsf{Mod( Q, Cat)}$ consisting of
* categories which have a free model of $\mathsf{Q}$ of objects, and
* functors whose object component is the unique extension of a function between the generating sets.
This may seem like an ugly category, but I'm convinced it's necessary. The freeness of the objects of the objects in $\mathsf{Q}$-$\mathsf{Cat}$ arise because $\mathsf{Q}$-nets have a free model of $\mathsf{Q}$ of species. Just like Petri nets, for a $\mathsf{Q}$-net $P$, $F_{\mathsf{Q}} P$ is a category where the morphisms represent all possible process which can be built using the transitions of $P$, the operations of $\mathsf{Q}$, and composition.
Although I don't do this yet, this formalism can be used to efficiently generate new variants of Petri nets which follow some set of algebraic rules. The above adjunction means that these nets are equipped with an out of the box description of their operational semantics. I'm just starting to explore $\mathsf{Q}$-nets and I'm excited to see what else they can do.
Many of the categories here are familiar to the Petri net community.
* $\mathsf{SEMILAT}$-$\mathsf{Net}$ is the category of elementary net systems. These are Petri nets which can have a maximum of one token in each place. Elementary net systems are used to represent non-concurrent programs; the location of the token represents how far along the computer is in execution.
* $\mathsf{Petri}$ is the good old category of Petri nets.
* $\mathsf{PreNet}$ is the category of pre-nets; Petri nets which are equipped with an ordering of the places on their input and output. These are useful for keeping track of causality in sequences of processes.
* $\mathbb{Z}$-$\mathsf{Net}$ is the category of [integer nets](https://arxiv.org/abs/1805.05988). These are [lending Petri nets](https://www.sciencedirect.com/science/article/pii/S0167642315001021) without a few properties. Integer nets and lending Petri nets are useful for modeling credit and borrowing. Places can hold negative tokens which represent debt.
Some of the functors in this diagram are known. $c$-$\mathsf{Net}$ and $e$-$\mathsf{Net}$ are commonly referred to as **abelianization**. This is because the $c$-$\mathsf{Net}$ sends a pre-net to the Petri net with an abelianized free monoid of places by forgetting about the ordering on the input and output of each species. $e$-$\mathsf{Net}$ is an analogous functor for $\mathbb{Z}$-$\mathsf{Net}$ and their non-commutative cousin $\mathsf{GRP}$-$\mathsf{Net}$.
This all sounds great but definitions are cheap. To justify a generalization can show that in its examples familiar consequences follow. Petri nets present free commutative monoidal categories: i.e., there is a meaningful adjunction between the category of Petri nets and a category where the objects are commutative monoidal categories. Commutative monoidal categories are symmetric monoidal categories whose symmetries are given by the identity. If you prefer, you can think of commutative monoidal categories categories as commutative monoid objects in $\mathsf{Cat}$.
This statement can be seen as a justification of the usefulness of Petri nets, because symmetric monoidal categories are the language of processes which can be done in sequence and in parallel. This adjunction makes precise the way in which Petri nets represent processes and gives a mathematical description of the way transitions shuffle tokens around in a Petri net. For a Petri net $P$, the free commutative monoidal category on $P$ is a category where the objects are all possible token configurations and the morphisms are all possible processes which bring one token configuration to another.
If the definition of $\mathsf{Q}$-$\mathsf{Net}$ is any good we should have a similar statement for $\mathsf{Q}$-nets. Indeed, $\mathsf{Q}$-nets present free models of $\mathsf{Q}$ in $\mathsf{Cat}$. There is an adjunction
$$F_{\mathsf{Q}} \dashv U_{\mathsf{Q}} \colon\mathsf{Q}\text{-}\mathsf{Net} \to \mathsf{Q}\text{-}\mathsf{Cat}$$
where $\mathsf{Q}$-$\mathsf{Cat}$ is the subcategory of $\mathsf{Mod( Q, Cat)}$ consisting of
* categories which have a free model of $\mathsf{Q}$ of objects, and
* functors whose object component is the unique extension of a function between the generating sets.
This may seem like an ugly category, but I'm convinced it's necessary. The freeness of the objects of the objects in $\mathsf{Q}$-$\mathsf{Cat}$ arise because $\mathsf{Q}$-nets have a free model of $\mathsf{Q}$ of species. Just like Petri nets, for a $\mathsf{Q}$-net $P$, $F_{\mathsf{Q}} P$ is a category where the morphisms represent all possible process which can be built using the transitions of $P$, the operations of $\mathsf{Q}$, and composition.
Although I don't do this yet, this formalism can be used to efficiently generate new variants of Petri nets which follow some set of algebraic rules. The above adjunction means that these nets are equipped with an out of the box description of their operational semantics. I'm just starting to explore $\mathsf{Q}$-nets and I'm excited to see what else they can do. where
* $\mathsf{SEMILAT}$ is the Lawvere theory of semi-lattices i.e. idempotent commutative monoids,
* $\mathsf{CMON}$ is the Lawvere theory of commutative monoids,
* $\mathsf{MON}$ is the Lawvere theory of monoids,
* $\mathsf{ABGRP}$ is the Lawvere theory of abelian groups and,
* $\mathsf{GRP}$ is the Lawvere theory of groups.
I won't say what the functors in this diagram are except that they are the most natural functors of their type; I refer you to my paper to see what they actually are. This diagram induces the following diagram of categories using the functor $(-)$-$\mathsf{Net}$:
where
* $\mathsf{SEMILAT}$ is the Lawvere theory of semi-lattices i.e. idempotent commutative monoids,
* $\mathsf{CMON}$ is the Lawvere theory of commutative monoids,
* $\mathsf{MON}$ is the Lawvere theory of monoids,
* $\mathsf{ABGRP}$ is the Lawvere theory of abelian groups and,
* $\mathsf{GRP}$ is the Lawvere theory of groups.
I won't say what the functors in this diagram are except that they are the most natural functors of their type; I refer you to my paper to see what they actually are. This diagram induces the following diagram of categories using the functor $(-)$-$\mathsf{Net}$:
 Many of the categories here are familiar to the Petri net community.
* $\mathsf{SEMILAT}$-$\mathsf{Net}$ is the category of elementary net systems. These are Petri nets which can have a maximum of one token in each place. Elementary net systems are used to represent non-concurrent programs; the location of the token represents how far along the computer is in execution.
* $\mathsf{Petri}$ is the good old category of Petri nets.
* $\mathsf{PreNet}$ is the category of pre-nets; Petri nets which are equipped with an ordering of the places on their input and output. These are useful for keeping track of causality in sequences of processes.
* $\mathbb{Z}$-$\mathsf{Net}$ is the category of [integer nets](https://arxiv.org/abs/1805.05988). These are [lending Petri nets](https://www.sciencedirect.com/science/article/pii/S0167642315001021) without a few properties. Integer nets and lending Petri nets are useful for modeling credit and borrowing. Places can hold negative tokens which represent debt.
Some of the functors in this diagram are known. $c$-$\mathsf{Net}$ and $e$-$\mathsf{Net}$ are commonly referred to as **abelianization**. This is because the $c$-$\mathsf{Net}$ sends a pre-net to the Petri net with an abelianized free monoid of places by forgetting about the ordering on the input and output of each species. $e$-$\mathsf{Net}$ is an analogous functor for $\mathbb{Z}$-$\mathsf{Net}$ and their non-commutative cousin $\mathsf{GRP}$-$\mathsf{Net}$.
This all sounds great but definitions are cheap. To justify a generalization can show that in its examples familiar consequences follow. Petri nets present free commutative monoidal categories: i.e., there is a meaningful adjunction between the category of Petri nets and a category where the objects are commutative monoidal categories. Commutative monoidal categories are symmetric monoidal categories whose symmetries are given by the identity. If you prefer, you can think of commutative monoidal categories categories as commutative monoid objects in $\mathsf{Cat}$.
This statement can be seen as a justification of the usefulness of Petri nets, because symmetric monoidal categories are the language of processes which can be done in sequence and in parallel. This adjunction makes precise the way in which Petri nets represent processes and gives a mathematical description of the way transitions shuffle tokens around in a Petri net. For a Petri net $P$, the free commutative monoidal category on $P$ is a category where the objects are all possible token configurations and the morphisms are all possible processes which bring one token configuration to another.
If the definition of $\mathsf{Q}$-$\mathsf{Net}$ is any good we should have a similar statement for $\mathsf{Q}$-nets. Indeed, $\mathsf{Q}$-nets present free models of $\mathsf{Q}$ in $\mathsf{Cat}$. There is an adjunction
$$F_{\mathsf{Q}} \dashv U_{\mathsf{Q}} \colon\mathsf{Q}\text{-}\mathsf{Net} \to \mathsf{Q}\text{-}\mathsf{Cat}$$
where $\mathsf{Q}$-$\mathsf{Cat}$ is the subcategory of $\mathsf{Mod( Q, Cat)}$ consisting of
* categories which have a free model of $\mathsf{Q}$ of objects, and
* functors whose object component is the unique extension of a function between the generating sets.
This may seem like an ugly category, but I'm convinced it's necessary. The freeness of the objects of the objects in $\mathsf{Q}$-$\mathsf{Cat}$ arise because $\mathsf{Q}$-nets have a free model of $\mathsf{Q}$ of species. Just like Petri nets, for a $\mathsf{Q}$-net $P$, $F_{\mathsf{Q}} P$ is a category where the morphisms represent all possible process which can be built using the transitions of $P$, the operations of $\mathsf{Q}$, and composition.
Although I don't do this yet, this formalism can be used to efficiently generate new variants of Petri nets which follow some set of algebraic rules. The above adjunction means that these nets are equipped with an out of the box description of their operational semantics. I'm just starting to explore $\mathsf{Q}$-nets and I'm excited to see what else they can do.
Many of the categories here are familiar to the Petri net community.
* $\mathsf{SEMILAT}$-$\mathsf{Net}$ is the category of elementary net systems. These are Petri nets which can have a maximum of one token in each place. Elementary net systems are used to represent non-concurrent programs; the location of the token represents how far along the computer is in execution.
* $\mathsf{Petri}$ is the good old category of Petri nets.
* $\mathsf{PreNet}$ is the category of pre-nets; Petri nets which are equipped with an ordering of the places on their input and output. These are useful for keeping track of causality in sequences of processes.
* $\mathbb{Z}$-$\mathsf{Net}$ is the category of [integer nets](https://arxiv.org/abs/1805.05988). These are [lending Petri nets](https://www.sciencedirect.com/science/article/pii/S0167642315001021) without a few properties. Integer nets and lending Petri nets are useful for modeling credit and borrowing. Places can hold negative tokens which represent debt.
Some of the functors in this diagram are known. $c$-$\mathsf{Net}$ and $e$-$\mathsf{Net}$ are commonly referred to as **abelianization**. This is because the $c$-$\mathsf{Net}$ sends a pre-net to the Petri net with an abelianized free monoid of places by forgetting about the ordering on the input and output of each species. $e$-$\mathsf{Net}$ is an analogous functor for $\mathbb{Z}$-$\mathsf{Net}$ and their non-commutative cousin $\mathsf{GRP}$-$\mathsf{Net}$.
This all sounds great but definitions are cheap. To justify a generalization can show that in its examples familiar consequences follow. Petri nets present free commutative monoidal categories: i.e., there is a meaningful adjunction between the category of Petri nets and a category where the objects are commutative monoidal categories. Commutative monoidal categories are symmetric monoidal categories whose symmetries are given by the identity. If you prefer, you can think of commutative monoidal categories categories as commutative monoid objects in $\mathsf{Cat}$.
This statement can be seen as a justification of the usefulness of Petri nets, because symmetric monoidal categories are the language of processes which can be done in sequence and in parallel. This adjunction makes precise the way in which Petri nets represent processes and gives a mathematical description of the way transitions shuffle tokens around in a Petri net. For a Petri net $P$, the free commutative monoidal category on $P$ is a category where the objects are all possible token configurations and the morphisms are all possible processes which bring one token configuration to another.
If the definition of $\mathsf{Q}$-$\mathsf{Net}$ is any good we should have a similar statement for $\mathsf{Q}$-nets. Indeed, $\mathsf{Q}$-nets present free models of $\mathsf{Q}$ in $\mathsf{Cat}$. There is an adjunction
$$F_{\mathsf{Q}} \dashv U_{\mathsf{Q}} \colon\mathsf{Q}\text{-}\mathsf{Net} \to \mathsf{Q}\text{-}\mathsf{Cat}$$
where $\mathsf{Q}$-$\mathsf{Cat}$ is the subcategory of $\mathsf{Mod( Q, Cat)}$ consisting of
* categories which have a free model of $\mathsf{Q}$ of objects, and
* functors whose object component is the unique extension of a function between the generating sets.
This may seem like an ugly category, but I'm convinced it's necessary. The freeness of the objects of the objects in $\mathsf{Q}$-$\mathsf{Cat}$ arise because $\mathsf{Q}$-nets have a free model of $\mathsf{Q}$ of species. Just like Petri nets, for a $\mathsf{Q}$-net $P$, $F_{\mathsf{Q}} P$ is a category where the morphisms represent all possible process which can be built using the transitions of $P$, the operations of $\mathsf{Q}$, and composition.
Although I don't do this yet, this formalism can be used to efficiently generate new variants of Petri nets which follow some set of algebraic rules. The above adjunction means that these nets are equipped with an out of the box description of their operational semantics. I'm just starting to explore $\mathsf{Q}$-nets and I'm excited to see what else they can do.