


|
|

|
Now let's talk about building the Leech lattice from integral octonions!
The Leech lattice is a marvelous thing. Here are three ways to define it:
Take a bunch of balls of radius one in 24 dimensions. Get as many balls to touch a single ball as you possibly can. Then, get as many balls to touch these as you possibly can. Go on like this forever. Unlike in 3 dimensions, you have no real choice about how to do this: the balls will inevitably be centered at points of the Leech lattice.
Take disks of radius one in the plane and pack them in the densest possible lattice arrangement. Use this pattern to form a layer of balls in 3 dimensions. Stack layers like this on top of each other, pushing them down to get the densest possible lattice packing of 3d balls. Use this pattern to form a layer of balls in 4 dimensions! Stack layers like this on top of each other, pushing them down to get the densest possible lattice packing of 4d balls. Repeat this until you get to 24 dimensions. There will be some choices — but no matter how you make these choices, you'll inevitably be led to the Leech lattice.
Up to isometry, the Leech lattice is the unique even unimodular lattice in 24 dimensions whose shortest nonzero vectors have length 2.
Since the Leech lattice lives in 24 dimensions and octonions live in 8, we should try to describe points in the Leech lattice using triples of octonions.
That's what Geoffrey Dixon and Robert Wilson did:
As a spinoff, this explains why there are
$$ 3 \cdot 240 \cdot (1 + 16 + 16^2) = 196,560$$
shortest nonzero vectors in the Leech lattice. 240 is the number of shortest nonzero vectors in the \(\mathrm{E}_8\) lattice — or in other words, the number of integral octonions of norm 1. The formula above was known, but not the explanation.
In a further paper, he used his idea to give an octonionic description of the symmetries of the Leech lattice:
If you take all the rotations and reflections that are symmetries of the Leech lattice, they generate a group called \(\mathrm{Co}_0\) with
$$ 8,315,553,613,086,720,000 $$
elements. This is not a simple group, because it contains the transformation \(x \mapsto -x\), which commutes with everything else. But when you mod out by that, you get a simple group called \(\mathrm{Co}_1\). This is half as big, with only
$$ 4,157,776,806,543,360,000 $$
elements. It's one of the most important sporadic finite simple groups!
All of this sounds quite fun, though also quite terrifying.
Luckily, Greg Egan found a way to simplify Wilson's ideas in a comment to Part 8. So, let me describe Egan's construction, and then reprint his proof that it works.
Egan took Wilson's construction and showed how to eliminate all mention of the octonions, focusing simply on the \(\mathrm{E}_8\) lattice. Here's one way to state Egan's result:
Theorem. Let \(L_0 \subseteq \mathbb{R}^8\) be the \(\mathrm{E}_8\) lattice, and let \(r_1, \dots, r_8 \in L_0\) be a basis of simple roots. There exists a rotation
$$R : \mathbb{R}^8 \to \mathbb{R}^8$$
such that:
For any rotation \(R\) with these properties, define lattices
$$ L_1 = T_1 L_0, \qquad L_2 = T_2 L_0 $$
Then the lattice consisting of all triples \((a,b,c) \in \mathbb{R}^{24}\) such that:
$$a, b, c \in L_0$$ $$a+b, a+c, b+c \in L_1$$ $$a+b+c \in L_2$$
is isometric to a copy of the Leech lattice that has been rescaled by a factor of \(\sqrt{2}\).
Proof. See below. \(\blacksquare\)
Here's the picture in my head:
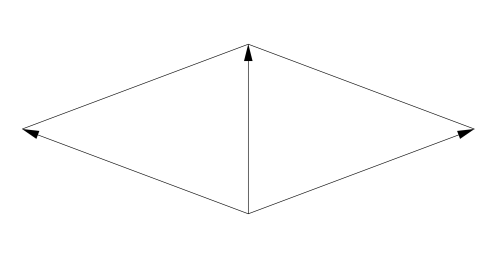
The vertical vector is the root \(r_i\). It has length \(\sqrt{2}\), as roots of \(\mathrm{E}_8\) do. The other two vectors are \(w_{i,1}\) and \(w_{i,2}\). They have length 2 and their dot product with \(r_i\) is 1. And in fact, their sum is \(r_i\).
Why? Since they've been formed by rescaling \(r_i\) and then rotating the result in opposite directions, their sum must be some number times \(r_i\). But since this sum has dot product 2 with \(r_i\), and so does \(r_i\) itself, that number must be 1.
Of course, the neat part is that all 24 vectors — the \(r_i\), the \(w_{1,i}\) and the \(w_{2,i}\) — all live in the same \(\mathrm{E}_8\) lattice.
So, if we want, we can take them to be integral octonions! We have to be careful: the integral octonions \(\mathbf{O}\) form a lattice that's a copy of the \(\mathrm{E}_8\) lattice rescaled by \(1/\sqrt{2}\). But luckily, this cancels the factor of \(\sqrt{2}\) in the theorem above. So, Egan's construction gives a copy of the Leech lattice at its correct scale as a sublattice of \(\mathbf{O}^3\)!
To understand why his construction works, we can't do better than read what he wrote. So, in everything that follows — even in the 'postscript' at the end — I'll just be quoting him.
by Greg Egan
I recently read Robert Wilson's beautiful paper Octonions and the Leech lattice, which constructs the Leech lattice as a sublattice of the space of triples of a certain set of octonions.
The particular set of octonions Wilson chooses to work with are not Cayley integral octonions, so they are not closed under multiplication. However, I realised that it's quite easy to tweak his construction to work with (any of the seven sets of) Cayley integral octonions instead. What's more, the geometrical aspects of his construction can be abstracted away from the octonionic aspects, giving a nice way to produce the Leech lattice (up to a rescaling) as a sublattice of \(L_0^3\), where \(L_0\) is any lattice isomorphic (up to a rescaling) to \(\mathrm{E}_8\).
So, suppose \(L_0\) is either isomorphic to \(\mathrm{E}_8\), or to some multiple of \(\mathrm{E}_8\). For the sake of concreteness, I will illustrate what follows using a specific example, the lattice generated by the rows of this matrix, which we will call \(r_1,\dots,r_8\):
$$r_i=\left( \begin{array}{cccccccc} -1 & -1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & -1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & -1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{array}\right)$$
These vectors have squared norms of 2, which is the usual normalisation convention for \(\mathrm{E}_8\), and they comprise a set of simple roots whose mutual dot products are \(-1\) for roots joined by an edge in the Dynkin diagram for \(\mathrm{E}_8\), and 0 otherwise.
In this lattice, the shortest non-zero vectors have squared norms of 2, and the next-shortest vectors have squared norms of 4, i.e. they are \(\sqrt{2}\) larger. For every simple root \(r_i\), there are numerous vectors \(w_{i,j}\) of squared norm 4 for which \(r_i\cdot w_{i,j}=1\). (In fact there are 576 such vectors in every case, but that particular number is not important.) If we were dealing with a differently scaled lattice, then this dot product would be different, of course, so the scale-invariant aspect here is that the angle between \(r_i\) and all these \(w_{i,j}\) is \(\arccos{\frac{1}{2\sqrt{2}}}\).
The \(w_{i,j}\) split up into pairs that lie precisely opposite each other with respect to \(r_i\), with all three vectors lying in the same plane. In fact, because of the particular angle, \(\arccos{\frac{1}{2\sqrt{2}}}\), between the vectors and the ratio of \(\sqrt{2}\) between their lengths, the sum of the two \(w_{i,j}\) in each such pair is simply equal to \(r_i\).
Now, we have so many choices of these pairs of \(w_{i,j}\) that we can find an ordered pair \((w_{i,1}, w_{i,2})\) for every root \(r_i\) such that the vectors \(w_{i,1}\) all lie at the same angles to each other as the corresponding \(r_i\), and so do the second members of each pair, \(w_{i,2}\). The mutual dot products between these vectors will be twice as large as those of the \(r_i\), but in other respects they just follow the \(\mathrm{E}_8\) Dynkin diagram as usual.
We will define \(L_1\) to be the lattice generated by the eight \(w_{i,1}\) and \(L_2\) to be the lattice generated by the eight \(w_{i,2}\); both these lattices are sublattices of \(L_0\) that are isomorphic to a version of \(\mathrm{E}_8\) that is \(\sqrt{2}\) larger than that of \(L_0\) itself.
To prove that such sets of vectors really exist, here is an example. (I haven't calculated how many different choices there are, but the number runs at least into the thousands.)
$$ w_{i,1}=\left( \begin{array}{rrrrrrrr} 0 & -1 & 1 & 1 & 1 & 0 & 0 & 0 \\ -1 & 0 & -1 & 0 & -1 & 1 & 0 & 0 \\ -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{3}{2} & \frac{1}{2} & \frac{1}{2} \\ 1 & -1 & 0 & 0 & -1 & 0 & 0 & -1 \\ 0 & 1 & -1 & 1 & 1 & 0 & 0 & 0 \\ -\frac{1}{2} & \frac{1}{2} & \frac{3}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{3}{2} & \frac{1}{2} \\ 0 & -1 & 0 & -1 & 0 & 0 & -1 & 1 \end{array} \right)$$
$$w_{i,2}=\left( \begin{array}{rrrrrrrr} -1 & 0 & -1 & -1 & -1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & -1 & 0 & 0 \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{3}{2} & -\frac{1}{2} & -\frac{1}{2} \\ -1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & -1 & 1 & -1 & 0 & -1 & 0 & 0 \\ \frac{1}{2} & -\frac{1}{2} & -\frac{3}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & -\frac{3}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & \frac{3}{2} & -\frac{1}{2} \end{array} \right)$$
It's not hard to check that for any \(i\), we have \(w_{i,1}+w_{i,2} = r_i\), that \(w_{i,1}\cdot r_i = w_{i,2}\cdot r_i = 1\), and the individual sets \(\{w_{i,1}\}\) and \(\{w_{i,2}\}\) generate lattices \(L_1\) and \(L_2\) that are versions of \(\mathrm{E}_8\) larger by a factor of \(\sqrt{2}\) than the version generated by \(\{r_i\}\).
Because of the geometry of the roots of these three lattices as we've defined them, we can concisely capture the relationship between the lattices themselves as follows. We define a linear operator \(R\) by the requirement that:
$$R w_{i,1} = \sqrt{2} r_i, \quad i=1,\dots,8$$
That is, in each plane spanned by \(w_{i,1}\) and \(r_i\), \(R\) rotates by an angle of \(\arccos{\frac{1}{2\sqrt{2}}}\). But \(w_{i,2}\) lies in that same plane, separated from \(r_i\) by the same angle, so we have:
$$R^2 w_{i,1} = R \sqrt{2} r_i = w_{i,2},\quad i=1,\dots,8$$
The entire lattices generated by these vectors are related in the same fashion. We will write this as:
$$T_1 L_0 = L_1, \quad T_2 L_0 = L_2$$
where we have now defined:
$$T_1 = \sqrt{2} R^{-1}, \quad T_2 = \sqrt{2} R$$
We also have the nice relation, which follows from \(w_{i,1}+w_{i,2}=r_i\), that:
$$T_1 + T_2 = I$$
We've now reached the point where we can make use of Wilson's construction. Wilson showed (using octonionic methods, and his own particular choice of the lattices I'm calling \(L_0\), \(L_1\) and \(L_2\)) that:
Theorem. The lattice \(L_L\) consisting of all triples \((a,b,c)\) such that:
$$a, b, c \in L_0$$ $$a+b, a+c, b+c \in L_1$$ $$a+b+c \in L_2$$
is isomorphic to a version of the Leech lattice which is rescaled by \(\sqrt{2}\) times the scaling of \(L_0\) relative to \(\mathrm{E}_8\).
Proof. For our concrete example where the roots of \(L_0\) have squared norm 2, we will get a lattice \(L_L\) from the construction that is \(\sqrt{2}\) times larger than the Leech lattice as it is normally defined. In the following, I will only talk about the particular scaling where \(L_0\) is isomorphic to \(\mathrm{E}_8\), but it's trivial to rescale everything in sight to suit any particular application where we want \(L_0\) to be larger or smaller.
To prove the claimed result, it suffices to show that \(L_L / \sqrt{2}\) is an even unimodular lattice with no vectors of squared norm 2, since the Leech lattice is the unique 24-dimensional lattice with these properties. An even lattice is one where every vector's squared norm is an even integer, and a unimodular lattice is one where the determinant of any basis is \(\pm 1\). But rather than requiring a basis, we will use an equivalent property: every unimodular lattice is self-dual. The dual of a lattice \(L\) is the set of vectors \(d\) such that for every \(v\in L\), the dot product \(d\cdot v\) is an integer. That set is precisely the original lattice if and only if the lattice is unimodular.
To proceed, we start from the well-known fact that \(\mathrm{E}_8\) itself is unimodular, and so \(L_0\) will be self-dual. The dual of \(L_1\), because of its different scaling, will be \(\frac{1}{2} L_1\), and the dual of \(L_2\) will be \(\frac{1}{2} L_2\).
If you ponder the definition of a dual lattice, you'll see that the dual of the intersection of two lattices is the lattice spanned by all the vectors in the individual duals. So, the dual of \(L_1 \cap L_2\) is the lattice spanned by \(\frac{1}{2} L_1\) and \(\frac{1}{2} L_2\), which certainly includes the entire lattice \(\frac{1}{2} L_0\), since every one of the \(r_i\) that generates \(L_0\) can be written as the sum of \(w_{i,1}\) in \(L_1\) and \(w_{i,2}\) in \(L_2\). But since \(L_1, L_2 \subset L_0\), the span of \(\frac{1}{2} L_1\) and \(\frac{1}{2} L_2\) can be no larger than \(\frac{1}{2} L_0\) and must be precisely equal to it. Taking duals, we then have:
$$2 L_0 = L_1 \cap L_2$$
This result lets us see that our criteria for membership of \(L_L\) are still satisfied if we change the sign of any element in \((a,b,c)\); say we change \(c\) to \(-c\). Clearly the first condition, \(a, b, -c \in L_0\), is still satisfied. For the second, we now have \(a-c = (a+c) - 2c\) that needs to be in \(L_1\), but since \(c \in L_0\) we have \(2c \in L_1\), and hence \(a-c \in L_1\). Similarly, \(a+b-c = (a+b+c)-2c\) needs to be in \(L_2\), and because \(2c \in L_2\), it is.
The same result tells us that all vectors of the form:
$$(2\lambda, 0, 0), \quad \lambda \in L_0$$
and permutations are elements of \(L_L\).
Suppose we have some \((x,y,z) \in \mathrm{dual}(L_L)\). Then \((x,y,z)\cdot (2\lambda, 0, 0) = 2\lambda \cdot x\) must be an integer for all \(\lambda \in L_0\), so \(x \in \mathrm{dual}(2 L_0) = \frac{1}{2} L_0\), and similarly for \(y\) and \(z\).
Vectors of the form:
$$(T_2 \lambda, -\lambda, \lambda), \quad \lambda \in L_0$$
and permutations are also elements of \(L_L\), since \(T_2 \lambda \in L_2\), and \(T_2 \lambda - \lambda = -T_1 \lambda \in L_1\). Changing signs and permuting coordinates, we have \((-T_2 \lambda, \lambda, \lambda) + (\lambda, -T_2 \lambda, -\lambda) = (T_1 \lambda, T_1 \lambda, 0) \in L_L\) for all \(\lambda \in L_0\), or simply \((\mu, \mu, 0)\in L_L\) for all \(\mu \in L_1\).
This means the dot product \((x,y,z)\cdot (\mu,\mu,0)=(x+y)\cdot \mu\) must be an integer, for all \(\mu \in L_1\). The dual of \(L_1\) is \(\frac{1}{2} L_1\), so \(x+y \in \frac{1}{2} L_1\), and similarly for \(x+z\) and \(y+z\).
And we also have \((T_2 \lambda, \lambda, \lambda) + (0, -T_1 \lambda, -T_1 \lambda) = (T_2 \lambda, T_2 \lambda, T_2 \lambda) \in L_L\), or simply \((\nu, \nu, \nu) \in L_L\) for all \(\nu \in L_2\). The dot product \((x,y,z)\cdot (\nu,\nu,\nu)=(x+y+z)\cdot \nu\) must be an integer, for all \(\nu \in L_2\), and the dual of \(L_2\) is \(\frac{1}{2} L_2\), so \(x+y+z \in \frac{1}{2} L_2\).
What we have shown so far is that:
$$\mathrm{dual}(L_L) \subseteq \frac{1}{2} L_L$$
or equivalently:
$$\mathrm{dual}(L_L/\sqrt{2}) \subseteq L_L/\sqrt{2}$$
We want to make this an equality. Suppose \((x,y,z) \in \frac{1}{2} L_L\), so that \(x+y, x+z, y+z \in \frac{1}{2} L_1\) and \(x+y+z \in \frac{1}{2} L_2\). Then:
$$(x,y,z)\cdot (x,y,z) = (x+y)\cdot (x+y) + (x+z)\cdot (x+z) + (y+z)\cdot (y+z) - (x+y+z)\cdot (x+y+z)$$
The squared norms of vectors in \(L_1\) and \(L_2\) are multiples of four, so the squared norms of vectors in \(\frac{1}{2} L_1\) and \(\frac{1}{2} L_2\) are integers. So we have shown that any \((x,y,z) \in \frac{1}{2} L_L\) has a squared norm that is an integer.
It follows that \(L_L/\sqrt{2}\) is an even lattice, with all squared norms even integers. What's more, any dot product of two elements \(p, q \in L_L/\sqrt{2}\) can be written as:
$$p \cdot q = \frac{1}{2}\left((p+q)\cdot (p+q) - p \cdot p - q \cdot q\right)$$
Since all the squared norms here are even, the dot product must be an integer. Therefore every element of \(L_L/\sqrt{2}\) also lies in \(\mathrm{dual}(L_L/\sqrt{2})\), and we've proved that \(L_L/\sqrt{2}\) is self-dual and hence unimodular.
Suppose \(L_L/\sqrt{2}\) has a vector of squared norm 2, or equivalently, \(L_L\) has a vector of squared norm 4. Recall that for any \((a,b,c) \in L_L\) we have \(a, b, c \in L_0\), and the squared norms of non-zero vectors in \(L_0\) are all at least 2. If all three vectors were non-zero that would mean a squared norm of at least 6, so at least one vector, say \(c\), is zero. Then \(a+c=a\) and \(b+c=b\) must lie in \(L_1\), where the non-zero vectors have squared norms of at least 4, and if two vectors were non-zero that would mean a squared norm of at least 8. Our last chance, then, is a single non-zero vector, which must belong to \(L_1 \cap L_2 = 2 L_0\), giving it a squared norm of at least 8. So we've shown that \(L_L/\sqrt{2}\) has no vector with a squared norm of 2.
Putting together everything we now know about \(L_L/\sqrt{2}\), it must be the Leech lattice. \(\blacksquare\)
As a postscript to the construction I just described of the Leech lattice as a sublattice of \(L_0^3\) where \(L_0\) is isomorphic to some possibly rescaled version of \(\mathrm{E}_8\) ... if we want to set \(L_0\) to any of the seven lattices of Cayley integral octonions, which have roots of length 1, and hence are re-scaled from the usual \(\mathrm{E}_8\) by a factor of \(\frac{1}{\sqrt{2}}\), it turns out that we can always choose one of the larger sublattices of \(L_0\), say \(L_1\), to be equal to a certain well-known version of \(\mathrm{E}_8\): one where every vector consists solely of either integer coordinates or integers plus \(\frac{1}{2}\), and where the sum of the coordinates is an even integer. This is true regardless of which of the seven sets of Cayley integral octonions we choose for \(L_0\), because this 'well-known version' of \(\mathrm{E}_8\) is a sublattice of the Kirmse integers, and it is invariant under any permutation of its coordinates, including the coordinate-swaps that yield the various Cayley integers.
The second sublattice, \(L_2\), is then found by identifying the rotation \(R\) that maps \(L_1\) into \(\sqrt{2} L_0\) and applying it a second time, to give \(L_2 = R^2 L_1\).
You can also read comments on the n-Category Café, and make your own comments or ask questions there!

|
|

|