2.4 Spinors and Trialities

A nonassociative division algebra may seem like a strange thing to bother with, but the notion of triality makes it seem a bit more natural. The concept of duality is important throughout linear algebra. The concept of triality is similar, but considerably subtler. Given vector spaces $V_1$ and $V_2$, we may define a duality to be a bilinear map

$$f \maps V_1 \times V_2 \to \R$$

that is nondegenerate, meaning that if we fix either argument to any nonzero value, the linear functional induced on the other vector space is nonzero. Similarly, given vector spaces $V_1,V_2,$ and $V_3$, a triality is a trilinear map

$$t \maps V_1 \times V_2 \times V_3 \to \R$$

that is nondegenerate in the sense that if we fix any two arguments to any nonzero values, the linear functional induced on the third vector space is nonzero.

Dualities are easy to come by. Trialities are much rarer. For suppose we have a triality

$$t \maps V_1 \times V_2 \times V_3 \to \R .$$

By dualizing, we can turn this into a bilinear map

$$m \maps V_1 \times V_2 \to V_3^\ast$$

which we call 'multiplication'. By the nondegeneracy of our triality, left multiplication by any nonzero element of $V_1$ defines an isomorphism from $V_2$ to $V_3^\ast$. Similarly, right multiplication by any nonzero element of $V_2$ defines an isomorphism from $V_1$ to $V_3^\ast$. If we choose nonzero elements $e_1 \in V_1$ and $e_2 \in V_2$, we can thereby identify the spaces $V_1$, $V_2$ and $V_3^\ast$ with a single vector vector space, say $V$. Note that this identifies all three vectors $e_1 \in V_1$, $e_2 \in V_2$, and $e_1e_2 \in V_3^\ast$ with the same vector $e \in V$. We thus obtain a product

$$m \maps V \times V \to V$$

for which $e$ is the left and right unit. Since left or right multiplication by any nonzero element is an isomorphism, $V$ is actually a division algebra! Conversely, any division algebra gives a triality.

It follows from Theorem 3 that trialities only occur in dimensions 1, 2, 4, or 8. This theorem is quite deep. By comparison, Hurwitz's classification of normed division algebras is easy to prove. Not surprisingly, these correspond to a special sort of triality, which we call a 'normed' triality.

To be precise, a normed triality consists of inner product spaces $V_1, V_2, V_3$ equipped with a trilinear map $t \maps V_1 \times V_2 \times V_3 \to \R$ with

$$% latex2html id marker 1560 \vert t(v_1, v_2, v_3)\vert \le \Vert v_1\Vert \, \Vert v_2\Vert \, \Vert v_3 \Vert,$$

and such that for all $v_1, v_2$ there exists $v_3 \ne 0$ for which this bound is attained -- and similarly for cyclic permutations of $1,2,3$. Given a normed triality, picking unit vectors in any two of the spaces $V_i$ allows us to identify all three spaces and get a normed division algebra. Conversely, any normed division algebra gives a normed triality.

But where do normed trialities come from? They come from the theory of spinors! From Section 2.3, we already know that any $n$-dimensional normed division algebra is a representation of $\Cliff (n-1)$, so it makes sense to look for normed trialities here. In fact, representations of $\Cliff (n-1)$ give certain representations of $\Spin (n)$, the double cover of the rotation group in $n$ dimensions. These are called 'spinors'. As we shall see, the relation between spinors and vectors gives a nice way to construct normed trialities in dimensions 1, 2, 4 and 8.

To see how this works, first let $\Pin (n)$ be the group sitting inside $\Cliff (n)$ that consists of all products of unit vectors in $\R^n$. This group is a double cover of the orthogonal group $\OO (n)$, where given any unit vector $v \in \R^n$, we map both $\pm v \in \Pin (n)$ to the element of $\OO (n)$ that reflects across the hyperplane perpendicular to $v$. Since every element of $\OO (n)$ is a product of reflections, this homomorphism is indeed onto.

Next, let $\Spin (n) \subset \Pin (n)$ be the subgroup consisting of all elements that are a product of an even number of unit vectors in $\R^n$. An element of $\OO (n)$ has determinant 1 iff it is the product of an even number of reflections, so just as $\Pin (n)$ is a double cover of $\OO (n)$, $\Spin (n)$ is a double cover of $\SO (n)$. Together with a French dirty joke which we shall not explain, this analogy is the origin of the terms '$\Pin$' and 'pinor'.

Since $\Pin (n)$ sits inside $\Cliff (n)$, the irreps of $\Cliff (n)$ restrict to representations of $\Pin (n)$, which turn out to be still irreducible. These are again called pinors, and we know what they are from Table 3. Similarly, $\Spin (n)$ sits inside the subalgebra

$$\Cliff _0(n) \subseteq \Cliff (n)$$

consisting of all linear combinations of products of an even number of vectors in $\R^n$. Thus the irreps of $\Cliff _0(n)$ restrict to representations of $\Spin (n)$, which turn out to be still irreducible. These are called spinors -- but we warn the reader that this term is also used for many slight variations on this concept.

In fact, there is an isomorphism

$$\phi \maps \Cliff (n-1) \to \Cliff _0(n)$$

given as follows:

$$\phi(e_i) = e_i e_n , \qquad \qquad 1 \le i \le n-1 ,$$

where $\{e_i\}$ is an orthonormal basis for $\R^n$. Thus spinors in $n$ dimensions are the same as pinors in $n-1$ dimensions! Table 3 therefore yields the following table, where we use similar notation but with '$S$' instead of '$P$':

$n$	$\Cliff _0(n)$	irreps of $\Cliff _0(n)$
$1$	$\R$	$S_1 = \R$
$2$	$\C$	$S_2 = \C$
$3$	$\H$	$S_3 = \H$
$4$	$\H \oplus \H$	$S_4^+ = \H, \, S_4^- = \H$
$5$	$\H[2]$	$S_5 = \H^2$
$6$	$\C[4]$	$S_6 = \C^4$
$7$	$\R[8]$	$S_7 = \R^8$
$8$	$\R[8] \oplus \R[8]$	$S_8^+ = \R^8,\, S_8^- = \R^8$

Table 4 — Spinor Representations

We call $S_n^+$ and $S_n^-$ the right-handed and left-handed spinor representations. For $n > 8$ we can work out the spinor representations using Bott periodicity:

$$S_{n+8} \iso S_n \tensor \R^{16}$$

and similarly for right-handed and left-handed spinors.

Now, besides its pinor representation(s), the group $\Pin (n)$ also has an irrep where we first apply the 2-1 homomorphism $\Pin (n) \to \OO (n)$ and then use the obvious representation of $\OO (n)$ on $\R^n$. We call this the vector representation, $V_n$. As a vector space $V_n$ is just $\R^n$, and $\Cliff (n)$ is generated by $\R^n$, so we have an inclusion

$$V_n \hookrightarrow \Cliff (n) .$$

Using this, we can restrict the action of the Clifford algebra on pinors to a map

$$% latex2html id marker 1566 \begin{array}{lcc} m_n \maps ... ...maps & V_n \times P_n \to P_n & {\rm otherwise.} \end{array}$$

This map is actually an intertwining operator between representations of $\Pin (n)$. If we restrict the vector representation to the subgroup $\Spin (n)$, it remains irreducible. This is not always true for the pinor representations, but we can always decompose them as a direct sum of spinor representations. Applying this decomposition to the map $m_n$, we get a map

$$% latex2html id marker 1567 \begin{array}{lc} m_n \maps V... ... \maps V_n \times S_n \to S_n & {\rm otherwise.} \end{array}$$

All the spinor representations appearing here are self-dual, so we can dualize the above maps and reinterpret them as trilinear maps

$$% latex2html id marker 1568 \begin{array}{lc} t_n \maps V... ... \times S_n \times S_n \to \R & {\rm otherwise.} \end{array}$$

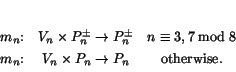
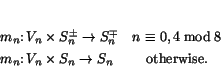
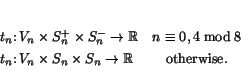
These trilinear maps are candidates for trialities! However, they can only be trialities when the dimension of the vector representation matches that of the relevant spinor representations. In the range of the above table this happens only for $n = 1,2,4,8$. In these cases we actually do get normed trialities, which in turn give normed division algebras:

$$% latex2html id marker 1569 \begin{array}{ll} t_1 \maps ... ...8^+ \times S_8^- \to \R & {\rm\; gives \;} \O . \end{array}$$

In higher dimensions, the spinor representations become bigger than the vector representation, so we get no more trialities this way — and of course, none exist.

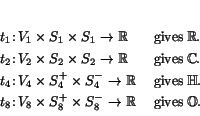
Of the four normed trialities, the one that gives the octonions has an interesting property that the rest lack. To see this property, one must pay careful attention to the difference between a normed triality and a normed division algebra. To construct a normed division $\K$ algebra from the normed triality $t \maps V_1 \times V_2 \times V_3 \to \R$, we must arbitrarily choose unit vectors in two of the three spaces, so the symmetry group of $\K$ is smaller than that of $t$. More precisely, let us define a automorphism of the normed triality $t \maps V_1 \times V_2 \times V_3 \to \R$ to be a triple of norm-preserving maps $f_i \maps V_i \to V_i$ such that

$$t(f_1(v_1), f_2(v_2), f_3(v_3)) = t(v_1,v_2,v_3)$$

for all $v_i \in V_i$. These automorphisms form a group we call $\Aut (t)$. If we construct a normed division algebra $\K$ from $t$ by choosing unit vectors $e_1 \in V_1, e_2 \in V_2$, we have

$$% latex2html id marker 1571 \Aut (\K) \iso \{(f_1,f_2,f_3)... ... \Aut (t)\; \colon \; f_1(e_1) = e_1, \; f_2(e_2) = e_2 \} .$$

In particular, it turns out that:

where

$$\OO (1) \iso \Z_2, \qquad \U (1) \iso \SO (2) , \qquad \Sp (1) \iso \SU (2)$$

are the unit spheres in $\R$, $\C$ and $\H$, respectively -- the only spheres that are Lie groups. $\G _2$ is just another name for the automorphism group of the octonions; we shall study this group in Section 4.1. The bigger group $\Spin (8)$ acts as automorphisms of the triality that gives the octonions, and it does so in an interesting way. Given any element $g \in \Spin (8)$, there exist unique elements $g_\pm \in \Spin (8)$ such that

$$t(g(v_1), g_+(v_2), g_-(v_3)) = t(v_1,v_2,v_3)$$

for all $v_1 \in V_8, v_2 \in S^+_8,$ and $v_3 \in S^-_8$. Moreover, the maps

$$\alpha_\pm \maps g \to g_\pm$$

are outer automorphisms of $\Spin (8)$. In fact ${\rm Out(\Spin (8))}$ is the permutation group on 3 letters, and there exist outer automorphisms that have the effect of permuting the vector, left-handed spinor, and right-handed spinor representations any way one likes; $\alpha_+$ and $\alpha_-$ are among these.

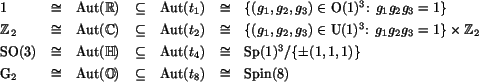
In general, outer automorphisms of simple Lie groups come from symmetries of their Dynkin diagrams. Of all the simple Lie groups, $\Spin (8)$ has the most symmetrical Dynkin diagram! It looks like this:

Here the three outer nodes correspond to the vector, left-handed spinor and right-handed spinor representations of $\Spin (8)$, while the central node corresponds to the adjoint representation — that is, the representation of $\Spin (8)$ on its own Lie algebra, better known as $\so (8)$. The outer automorphisms corresponding to the symmetries of this diagram were discovered in 1925 by Cartan [14], who called these symmetries triality. The more general notion of 'triality' we have been discussing here came later, and is apparently due to Adams [1].

The construction of division algebras from trialities has tantalizing links to physics. In the Standard Model of particle physics, all particles other than the Higgs boson transform either as vectors or spinors. The vector particles are also called 'gauge bosons', and they serve to carry the forces in the Standard Model. The spinor particles are also called 'fermions', and they correspond to the basic forms of matter: quarks and leptons. The interaction between matter and the forces is described by a trilinear map involving two spinors and one vector. This map is often drawn as a Feynman diagram:

where the straight lines denote spinors and the wiggly one denotes a vector. The most familiar example is the process whereby an electron emits or absorbs a photon.

It is fascinating that the same sort of mathematics can be used both to construct the normed division algebras and to describe the interaction between matter and forces. Could this be important for physics? One prima facie problem with this speculation is that physics uses spinors associated to Lorentz groups rather than rotation groups, due to the fact that spacetime has a Lorentzian rather than Euclidean metric. However, in Section 3.3 we describe a way around this problem. Just as octonions give the spinor representations of $\Spin (8)$, pairs of octonions give the spinor representations of $\Spin (9,1)$. This is one reason so many theories of physics work best when spacetime is 10-dimensional! Examples include superstring theory [26,42], supersymmetric gauge theories [31,60,78], and Geoffrey Dixon's extension of the Standard Model based on the algebra $\C \tensor \H \tensor \O$, in which the 3 forces arise naturally from the three factors in this tensor product [28].

home