Random Permutations

January 11, 2020

Random Permutations

John Baez

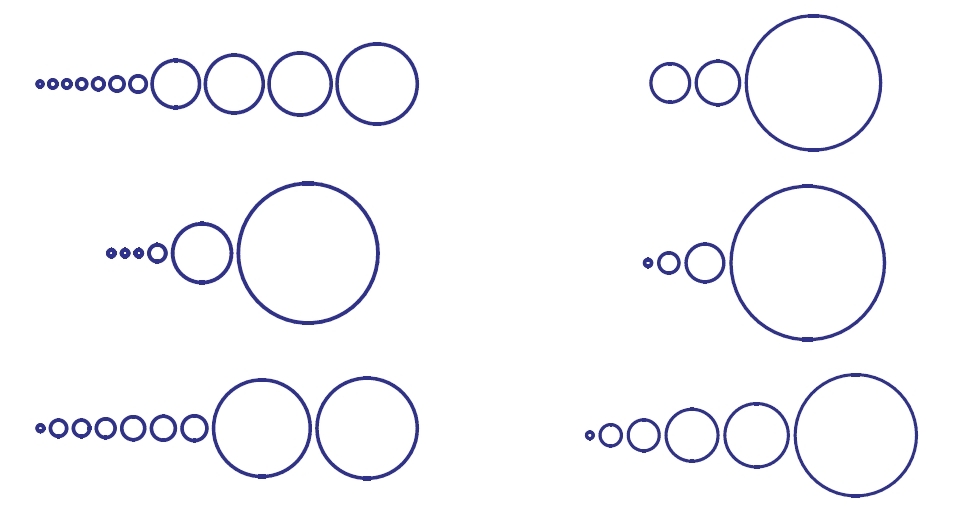Six random permutations of a 500-element set, where
circle areas are drawn in proportion to cycle lengths.
From Analytic Combinatorics by Flajolet and Sedgewick.

Say you randomly choose one of the n! permutations of a huge n-element set. What's it like, typically? This is actually many questions in one. Answering these questions uses a fascinating mix of elementary techniques, generating functions, and complex analysis. And the answers are often beautifully simple!

Part 0 — What's the average length of the longest cycle in a random permutation of an n-element set?

Part 1 — What is the probability that a randomly chosen permutation of an n-element set has exactly k fixed points?

Part 2 — What is the probability that the shortest cycle in a randomly chosen permutation of an n-element set has length greater than k?

Part 3 — A large collection of questions about random permutations, with answers.

Part 4 — What is the probability that a randomly chosen permutation of an n-element set has a cycle of length greater than \(n/2\)?

Part 5 — What is the average length of a cycle in a randomly chosen permutation of an n-element set?

Part 6 — What expected number of cycles of length k in a randomly chosen permutation of an n-element set?

Part 7 — How is the distribution of the number of cycles of length k in a random permutation related to a Poisson distribution?

Part 8 — What's the nth moment of a Poisson distribution?

Part 9 — If we treat the number of cycles of length k in a random permutation of an n-element set as a random variable, what do the moments of this random variable approach as n → ∞?

Part 10 — How to compute statistics of random permutations using groupoid cardinalities.

Part 11 — How to prove the Cycle Length Lemma, a fundamental result on random permutations, using groupoid cardinalities.

Part 12 — How to write the groupoid of finite sets equipped with a permutation as a sum over Young diagrams, and how to use this to compute the probability that a random permutation has given cycle lengths.

Part 13 — A groupoid slightly larger than the groupoid of finite sets equipped with permutation, and its connection to Poisson distributions.

Part 14 — A detailed self-contained account of how to prove the Cycle Length Lemma using groupoid cardinalities.

My own arguments emphasize the use of combinatorial species and their generating functions, so it will help if you know a bit about those. These books are helpful:

François Bergeron, Gilbert Labelle, and Pierre Leroux, Introduction to the Theory of Species of Structures.

Phillipe Flajolet and Robert Sedgewick, Analytic Combinatorics.

Herbert S. Wilf, Generatingfunctionology.