John Baez: The Most  Schmotons  John Baez: Ever wonder

John Baez: Perhaps the nicest Gaussian of all

Let's see. In my first reply to Michael Weiss' post I said a few words about coherent states. Let me say a few more general remarks about coherent states. Eventually in some later post I will turn towards the practical business at hand: calculating what coherent states look like in the basis given by eigenstates of the harmonic oscillator Hamiltonian. (Michael already did this, so I'll just say a bit about what he did.)

A coherent state is supposed to be roughly a ``best quantum approximation to a classical state''. There is a big theory of coherent states which makes this a lot more precise, but let's not get into that. Instead, let's just ponder what this might mean.

Classically, a particle on the line has a definite position q and momentum p, so it is described by a point in phase space, (q,p). Quantum mechanically, the more we know about position, the less we know about momentum, and vice versa. Our ability to know both at once is limited by Heisenberg's uncertainty principle:

Delta p   Delta q >= 1/2

(Here, as always in this thread, we are working in units where hbar is one, as well as the mass of our particle and the spring constant of our harmonic oscillator.)

Which states do the best job of simultaneously minimizing the uncertainty in position and momentum? Which states make Delta p  Delta q equal to 1/2? It turns out that these states are precisely the Gaussians, possibly translated, and possibly multiplied by a complex exponential.

Perhaps the nicest Gaussian of all is

exp(-x²/2)

since this is the ground state of the harmonic oscillator Hamiltonian, at least after we normalize it.

This function is its own Fourier transform (if we define our Fourier transform right). Since you can compute the uncertainty in momentum by taking the Fourier transform of your wavefunction and then computing the uncertainty in position of that, this Gaussian must have the same uncertainty in position as it does in momentum. If everything I've said so far is true, we must therefore have

Delta p = Delta q = 1/sq2 for this Gaussian.

Of course, there are lots of other Gaussians centered at the origin with Delta p  Delta q = 1/2 We can squish our Gaussian or stretch it out like this:

exp(-x²/2sigma)

The Fourier transform of a squished-in skinny Gaussian is a stretched-out squat Gaussian and vice versa. So all these Gaussians have

Delta p  Delta q = 1/2 but the one we chose is the only one where

Delta p = Delta q That can be our definition of a ``coherent state'': a state that simultaneously minimizes the uncertainty in position and momentum, and makes these uncertainties equal each other. Later we can think more about ``squeezed states'' where the uncertainties are not equal. There was recently a big fad where everyone was making squeezed states of light in the lab. But for now, we will not squeeze our states.

So: the Gaussian

exp(-x²/2)

is the primordial ``coherent state''. In this state, the expectation value of position is obviously zero, since the bump is symmetrically centered at the origin. The expectation value of momentum is also obviously zero, since:

1) the Fourier transform of this function is itself, so whatever applies to position applies to momentum as well,

or if you prefer,

2) the expectation value of momentum is zero for any real-valued wavefunction. (Hint: to see this, just use integration by parts.)

So exp(-x²/2) is a coherent state with expectation values

<p> = <q> = 0.

We can get lots more coherent states by taking this Gaussian and translating it in position space and/or momentum space. Translating in position space by c, we get a Gaussian

exp(-(x-c)²/2)

This is the coherent state I wanted Michael to express in terms of eigenstates of the harmonic oscillator Hamiltonian. This obviously has

< q> = c

and since it's real-valued it still has

< p> = 0.

Translating in momentum space by some amount b is the same as multiplying by a complex exponential e^ibx. Or, if you prefer, just take a Fourier transform, translate by b, and take an inverse Fourier transform. Same thing. If we do this to our primordial Gaussian bump, we get

exp(ibx-x²/2)

which is our coherent state with

<q> = 0

and

<p> = b.

Why does it still have <q> = 0? Well, we are just multiplying our Gaussian bump by a unit complex number or ``phase'' at each point, and this doesn't affect the expectation value of position.

Finally, we can translate in both position and momentum space directions. These two operations don't commute, of course, since the position and momentum operators don't commute, and momentum is the generator of translations in position space, while position is the generator of translations in momentum space (possibly up to an annoying minus sign).

What do we get? Well, take our bump and first translate it in position space by c:

 

exp(-(x-c)²/2)

and then in momentum space by b:

exp(ibx-(x-c)²/2)

Or, alternatively, first translate it in momentum space by b:

exp(ibx-x²/2)

and then in position space by c:

exp(ib(x-c)-(x-c)²/2)

I claim that these are equal up to a phase...one of them is e^ibc times the other. This is always how translatiions in position space and momentum space fail to commute.

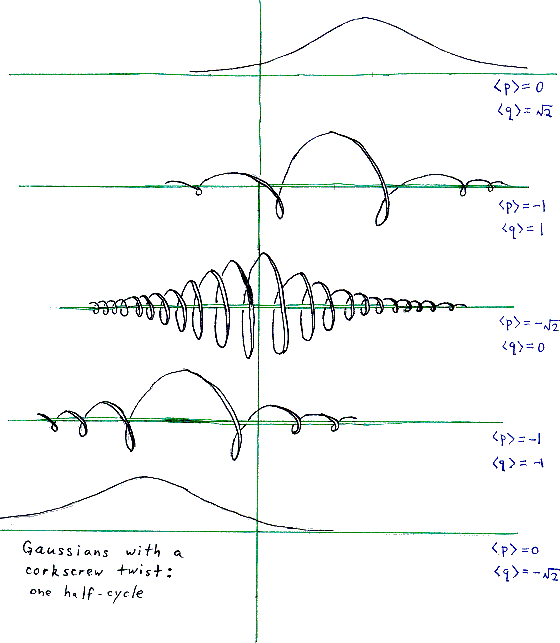
While terribly important in some ways, the phase is not such a big deal in other ways. (That's the weird thing about quantum mechanics when you are first learning it: sometimes a phase is very important, while other times it doesn't matter at all. Of course, it just depends what you're doing.) A phase times a coherent state is still a coherent state in my book. So we have gotten our hands on a coherent state with

<p> = b and

<q> = c

A translated Gaussian bump, with a corkscrew twist thrown in! I hope you visualize this thing for various values of b and c; it's a very pretty thing, and it will serve as our quantum ``best approximation'' to a particle with momentum b and position c.

Then, later, we will use a souped-up version of this as the quantum- field-theoretic ``best approximation'' to a particular state of a classical field theory, like electromagnetism.

3/10/1998