Bibliography

1

A. Ashtekar, Quantum mechanics of geometry, available as gr-qc/9901023.

2

M. F. Atiyah, The Geometry and Physics of Knots, Cambridge U. Press, Cambridge, 1990.

3

R. Baadhio and L. Kauffman, editors, Quantum Topology, World Scientific, Singapore, 1993.

4

J. Baez, Spin networks in nonperturbative quantum gravity, in The Interface of Knots and Physics, ed. L. Kauffman, American Mathematical Society, Providence, Rhode Island, 1996. Also available as gr-qc/9504036.

5

J. Baez, An introduction to 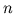$n$-categories, 7th Conference on Category Theory and Computer Science, eds. E. Moggi and G. Rosolini, Lecture Notes in Computer Science 1290, Springer Verlag, Berlin, 1997, pp. 1-33. Also available as q-alg/9705009.

6

J. Baez, Spin foam models, Class. Quantum Grav. 15 (1998), 1827-1858. Also available as gr-qc/9709052.

7

J. Baez and J. Dolan, Higher-dimensional algebra and topological quantum field theory, Jour. Math. Phys. 36 (1995), 6073-6105. Also available as q-alg/9503002.

8

J. Baez and J. Dolan, Categorification, in Higher Category Theory, eds. E. Getzler and M. Kapranov, American Mathematical Society, Providence, 1998, pp. 1-36. Also available as math.QA/9802029.

9

J. Barbour, Absolute or Relative Motion? A Study from the Machian Point of View of the Discovery and the Structure of Dynamical Theories pt. 1, Cambridge U. Press, Cambridge, 1989.

10

J. Barrett, Quantum gravity as topological quantum field theory, Jour. Math. Phys. 36 (1995), 6161-6179. Also available as gr-qc/9506070.

11

J. Barrett and L. Crane, Relativistic spin networks and quantum gravity, Jour. Math. Phys. 39 (1998), 3296-3302. Also available as gr-qc/9709028.

12

R. Brown, Out of line, Roy. Inst. Proc. 64 (1992), 207-243.

13

S. Carlip, Quantum Gravity in 2+1 Dimensions, Cambridge University Press, Cambridge, 1998.

14

L. Crane, 2-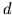$d$ Physics and 3-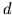$d$ topology, Commun. Math. Phys. 135 (1991), 615-640.

15

J. Earman, World Enough and Spacetime: Absolute vs. Relational Theories of Space and Time, MIT Press, Cambridge, 1989.

16

L. Freidel and K. Krasnov, Spin foam models and the classical action principle. Available as hep-th/9807092.

17

R. Goldblatt, Topoi, the Categorial Analysis of Logic, North-Holland, New York, 1979.

18

R. Helling and H. Nicolai, Supermembranes and (M)atrix theory. Available as hep-th/9809103.

19

L. Kauffman, Knots and Physics, World Scientific, Singapore, 1993.

20

R. Lawrence, Triangulation, categories and extended field theories, in Quantum Topology, eds. R. Baadhio and L. Kauffman, World Scientific, Singapore, 1993, pp. 191-208.

21

S. Mac Lane, Categories for the Working Mathematician, Springer, Berlin, 1988.

22

F. Markopoulou and L. Smolin, Quantum geometry with intrinsic local causality, Phys. Rev. D58: 084032. Also available as gr-qc/9712067.

23

M. Reisenberger, A left-handed simplicial action for Euclidean general relativity, available as gr-qc/9609002.

24

M. Reisenberger and C. Rovelli, ``Sum over surfaces'' form of loop quantum gravity, Phys. Rev. D56 (1997), 3490-3508. Also available as gr-qc/9612035.

25

C. Rovelli, What is observable in classical and quantum gravity?, Class. Quant. Grav. 8 (1991), 297-316.

26

C. Rovelli, Quantum reference systems, Class. Quant. Grav. 8 (1991), 317-331.

27

C. Rovelli, Halfway through the woods: contemporary research on space and time, in The Cosmos of Science: Essays of Exploration, eds. J. Earman and J. Norton, U. of Pittsburgh Press, Pittsburgh, 1997, pp. 180-223.

28

C. Rovelli, Loop quantum gravity, Living Reviews in Relativity (1998), available at http://www.livingreviews.org/Articles/Volume1/1998-1rovelli/index.html

29

L. Smolin, The future of spin networks, in The Geometric Universe: Science, Geometry, and the Work of Roger Penrose, eds. S. Huggett, Paul Tod, and L.J. Mason, Oxford University Press, 1998. Also available as gr-qc/9702030.

30

V. Turaev, Quantum Invariants of Knots and 3-Manifolds, de Gruyter, New York, 1994.

© 1999 John Baez
baez@math.removethis.ucr.andthis.edu

home