4. The Monoidal Category of Hilbert Spaces

An important goal of the enterprise of physics is to describe, not just one physical system at a time, but also how a large complicated system can be built out of smaller simpler ones. The simplest case is a so-called `joint system': a system built out of two separate parts. Our experience with the everyday world leads us to believe that to specify the state of a joint system, it is necessary and sufficient to specify states of its two parts. (Here and in what follows, by `states' we always mean what physicists call `pure states'.) In other words, a state of the joint system is just an ordered pair of states of its parts. So, if the first part has $S$ as its set of states, and the second part has $T$ as its set of states, the joint system has the cartesian product $S \times T$ as its set of states.

One of the more shocking discoveries of the twentieth century is that this is wrong. In both classical and quantum physics, given states of each part we get a state of the joint system. But only in classical physics is every state of the joint system of this form! In quantum physics are also `entangled' states, which can only be described as superpositions of states of this form. The reason is that in quantum theory, the states of a system are no longer described by a set, but by a Hilbert space. Moreover -- and this is really an extra assumption -- the states of a joint system are described not by the cartesian product of Hilbert spaces, but by their tensor product.

Quite generally, we can imagine using objects in any category to describe physical systems, and morphisms between these to describe processes. In order to handle joint systems, this category will need to have some sort of `tensor product' that gives an object $A \otimes B$ for any pair of objects $A$ and $B$. As we shall explain, categories of this sort are called `monoidal'. The category ${\rm Set}$ is a example where the tensor product is just the usual cartesian product of sets. Similarly, the category ${\rm Hilb}$ is a monoidal category where the tensor product is the usual tensor product of Hilbert spaces. However, these two examples are very different, because the product in ${\rm Set}$ is `cartesian' in a certain technical sense, while the product in ${\rm Hilb}$ is not. This turns out to explain a lot about why joint systems behave so counterintuively in quantum physics. Moreover, it is yet another way in which ${\rm Hilb}$ resembles $n{\rm Cob}$ more than ${\rm Set}$.

To see this in detail, it pays to go back to the beginning and think about cartesian products. Given two sets $S$ and $T$, we define $S \times T$ to be the set of all ordered pairs $(s,t)$ with $s \in S$ and $t \in T$. But what is an ordered pair? This depends on our approach to set theory. We can use axioms in which ordered pairs are a primitive construction, or we can define them in terms of other concepts. For example, in 1914, Wiener defined the ordered pair $(s,t)$ to be the set $\{ \{ \{s\}, \emptyset \}, \{ \{t\} \}$. In 1922, Kuratowski gave the simpler definition $(s,t) = \{ \{s\}, \{s,t\} \}$. We can use the still simpler definition $(s,t) = \{s,\{s,t\}\}$ if our axioms exclude the possibility of sets that contain themselves. Various other definitions have also been tried [17]. In traditional set theory we arbitrarily choose one approach to ordered pairs and then stick with it. Apart from issues of convenience or elegance, it does not matter which we choose, so long as it `gets the job done'. In other words, all these approaches are all just technical tricks for implementing our goal, which is to make sure that $(s,t) = (s',t')$ if and only if $s = s'$ and $t = t'$.

It is a bit annoying that the definition of ordered pair cannot get straight to the point and capture the concept without recourse to an arbitrary trick. It is natural to seek an approach that focuses more on the structural role of ordered pairs in mathematics and less on their implementation. This is what category theory provides.

The reason traditional set theory arbitarily chooses a specific implementation of the ordered pair concept is that it seems difficult to speak precisely about ``some thing $(s,t)$ -- I don't care what it is -- with the property that $(s,t) = (s',t')$ iff $s = s'$ and $t = t'$''. So, the first move in category theory is to stop focussing on ordered pairs and instead focus on cartesian products of sets. What properties should the cartesian product $S \times T$ have? To make our answer applicable not just to sets but to objects of other categories, it should not refer to elements of $S \times T$. So, the second move in category theory is to describe the cartesian product $S \times T$ in terms of functions to and from this set.

The cartesian product $S \times T$ has functions called `projections' to the sets $S$ and $T$:

$$p_1 \colon S \times T \rightarrow S , \qquad p_2 \colon S \times T \rightarrow T .$$

Secretly we know that these pick out the first or second component of any ordered pair in $S \times T$:

$$p_1(s,t) = s, \qquad p_2(s,t) = t .$$

But, our goal is to characterize the product by means of these projections without explicit reference to ordered pairs. For this, the key property of the projections is that given any element $s \in S$ and any element $t \in T$, there exists a unique element $x \in S \times T$ such that $p_1(x) = s$ and $p_2(x) = T$. Furthermore, as a substitute for elements of the sets $S$ and $T$, we can use functions from an arbitrary set to these sets.

Thus, given two sets $S$ and $T$, we define their cartesian product to be any set $S \times T$ equipped with functions $p_1 \colon S \times T \rightarrow S$, $p_2 \colon S \times T \rightarrow T$ such that for any set $X$ and functions $f_1 \colon X \rightarrow S$, $f_2 \colon X \rightarrow T$, there exists a unique function $f \colon X \rightarrow S \times T$ with

$$f_1 = p_1 f, \qquad f_2 = p_2 f.$$

Note that with this definition, the cartesian product is not unique! Wiener's definition of ordered pairs gives a cartesian product of the sets $S$ and $T$, but so does Kuratowski's, and so does any other definition that `gets the job done'. However, this does not lead to any confusion, since one can easily show that any two choices of cartesian product are isomorphic in a canonical way. For a proof of this and other facts about cartesian products, see for example the textbook by McLarty [27].

All this generalizes painlessly to an arbitrary category. Given two objects $A$ and $B$ in some category, we define their cartesian product (or simply product) to be any object $A \times B$ equipped with morphisms

$$p_1 \colon A \times B \rightarrow A, \qquad p_2 \colon A \times B \rightarrow B,$$

called projections, such that for any object $X$ and morphisms $f_1 \colon X \rightarrow A$, $f_2 \colon X \rightarrow B$, there is a unique morphism $f \colon X \rightarrow A \times B$ with $f_1 = p_1 f$ and $f_2 = p_2 f$. The product may not exist, and it may not be unique, but it is unique up to a canonical isomorphism. Category theorists therefore feel free to speak of `the' product when it exists.

We say a category has binary products if every pair of objects has a a product. One can also talk about $n$-ary products for other values of $n$, but a category with binary products has $n$-ary products for all $n \ge 1$, since we can construct these as iterated binary products. The case $n = 1$ is trivial, since the product of one object is just that object itself (up to canonical isomorphism). The only remaining case is $n = 0$. This is surprisingly important. A $0$-ary product is usually called a terminal object and denoted $1$: it is an object such that that for any object $X$ there exists a unique morphism from $X$ to $1$. Terminal objects are unique up to canonical isomorphism, so we feel free to speak of `the' terminal object in a category when one exists. The reason we denote the terminal object by $1$ is that in ${\rm Set}$, any set with one element is a terminal object. If a category has a terminal object and binary products, it has $n$-ary products for all $n$, so we say it has finite products.

It turns out that these concepts capture much of our intuition about joint systems in classical physics. In the most stripped-down version of classical physics, the states of a system are described as elements of a mere set. In more elaborate versions, the states of a system form an object in some fancier category, such as the category of topological spaces or manifolds. But, just like ${\rm Set}$, these fancier categories have finite products -- and we use this fact when describing the states of a joint system.

To sketch how this works in general, suppose we have any category with finite products. To do physics with this, we think of any of the objects of this category as describing some physical system. It sounds a bit vague to say that a physical system is `described by' some object $A$, but we can make this more precise by saying that states of this system are morphisms $f \colon 1 \rightarrow A$. When our category is ${\rm Set}$, a morphism of this sort simply picks out an element of the set $A$. In the category of topological spaces, a morphism of this sort picks out a point in the topological space $A$ -- and similarly for the category of manifolds, and so on. For this reason, category theorists call a morphism $f \colon 1 \rightarrow A$ an element of the object $A$.

Next, we think of any morphism $g \colon A \rightarrow B$ as a `process' carrying states of the system described by $A$ to states of the system described by $B$. This works as follows: given a state of the first system, say $f \colon 1 \rightarrow A$, we can compose it with $g$ to get a state of the second system, $gf \colon 1 \rightarrow B$.

Then, given two systems that are described by the objects $A$ and $B$, respectively, we decree that the joint system built from these is described by the object $A \times B$. The projection $p_1 \colon A \times B \rightarrow A$ can be thought of as a process that takes a state of the joint system and discards all information about the second part, retaining only the state of the first part. Similarly, the projection $p_2$ retains only information about the second part.

Calling these projections `processes' may strike the reader as strange, since `discarding information' sounds like a subjective change of our description of the system, rather than an objective physical process like time evolution. However, it is worth noting that in special relativity, time evolution corresponds to a change of coordinates $t \mapsto t + c$, which can also be thought of as change of our description of the system. The novelty in thinking of a projection as a physical process really comes, not from the fact that it is `subjective', but from the fact that it is not invertible.

With this groundwork laid, we can use the definition of `product' to show that a state of a joint system is just an ordered pair of states of each part. First suppose we have states of each part, say $f_1 \colon 1 \rightarrow A$ and $f_2 \colon 1 \rightarrow B$. Then there is a unique state of the joint system, say $f \colon 1 \rightarrow A \times B$, which reduces to the given state of each part when we discard information about the other part: $p_1 f = f_1$ and $p_2 f = f_2$. Conversely, every state of the joint system arises this way, since given $f \colon 1 \rightarrow A \times B$ we can recover $f_1$ and $f_2$ using these equations.

However, the situation changes drastically when we switch to quantum theory! The states of a quantum system can still be thought of as forming a set. However, we do not take the product of these sets to be the set of states for a joint quantum system. Instead, we describe states of a system as unit vectors in a Hilbert space, modulo phase. We define the Hilbert space for a joint system to be the tensor product of the Hilbert spaces for its parts.

The tensor product of Hilbert spaces is not a cartesian product in the sense defined above, since given Hilbert spaces $H$ and $K$ there are no linear operators $p_1 \colon H \otimes K \rightarrow H$ and $p_2 \colon H \otimes K \rightarrow K$ with the required properties. This means that from a (pure) state of a joint quantum system we cannot extract (pure) states of its parts. This is the key to Bell's `failure of local realism'. Indeed, under quite general conditions one can derive Bell's inequality from the assumption that pure states of a joint system determine pure states of its parts [3,8], so violations of Bell's inequality should be seen as an indication that this assumption fails.

The Wooters-Zurek argument that `one cannot clone a quantum state' [32] is also based on the fact that the tensor product of Hilbert spaces is not cartesian. To get some sense of this, note that whenever $A$ is an object in some category for which the product $A \times A$ exists, there is a unique morphism

$$\Delta \colon A \rightarrow A \times A$$

such that $p_1 \Delta = 1_A$ and $p_2 \Delta = 1_A$. This morphism is called the diagonal of $A$, since in the category of sets it is the map given by $\Delta(a) = (a,a)$ for all $a \in A$, whose graph is a diagonal line when $A$ is the set of real numbers. Conceptually, the role of a diagonal morphism is to duplicate information, just as the projections discard information. In applications to physics, the equations $p_1 \Delta = 1_A$ and $p_2 \Delta = 1_A$ says that if we duplicate a state in $A$ and then discard one of the two resulting copies, we are left with a copy identical to the original.

In ${\rm Hilb}$, however, since the tensor product is not a product in the category-theoretic sense, it makes no sense to speak of a diagonal morphism $\Delta \colon H \rightarrow H \otimes H$. In fact, a stronger statement is true: there is no natural (i.e. basis-independent) way to choose a linear operator from $H$ to $H \otimes H$ other than the zero operator. So, there is no way to duplicate information in quantum theory.

Since the tensor product is not a cartesian product in the sense explained above, what exactly is it? To answer this, we need the definition of a `monoidal category'. Monoidal categories were introduced by Mac Lane [23] in early 1960s, precisely in order to capture those features common to all categories equipped with a well-behaved but not necessarily cartesian product. Since the definition is a bit long, let us first present it and then discuss it:

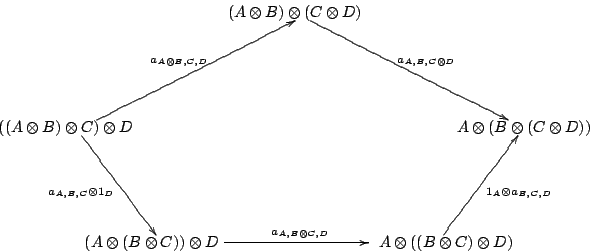
Definition. A monoidal category consists of:

(i)

a category ${\cal M}$,

(ii)

a functor $\otimes \colon {\cal M}\times {\cal M}\rightarrow {\cal M}$,

(iii)

a unit object $I \in {\cal M}$,

(iv)

natural isomorphisms called the associator:

$$a_{A,B,C} \colon (A \otimes B) \otimes C \rightarrow A \otimes (B \otimes C),$$

the left unit law:

$$\ell_A \colon I \otimes A \rightarrow A ,$$

and the right unit law:

$$r_A \colon A \otimes I \rightarrow A,$$

such that the following diagrams commute for all objects $A,B,C,D \in {\cal M}$:

(v)

$$\xy0 ;/r.30pc/: (0,20)*{(A \otimes B)\otimes (C \otimes D)... ...';''4''} {\ar^{a_{A \otimes B,C,D}} ''5'';''1''} \endxy \\$$

(vi)

$$\xymatrix{ (A \otimes I) \otimes B \ar[rr]^{a_{A,I,B}} \a... ...mes B) \ar[dl]^{1_A \otimes \ell_B } \\ & A \otimes B } \\$$

This obviously requires some explanation! First, it makes use of some notions we have not explained yet, ruining our otherwise admirably self-contained treatment of category theory. For example, what is ${\cal M} \times {\cal M}$ in clause (ii) of the definition? This is just the category whose objects are pairs of objects in ${\cal M}$, and whose morphisms are pairs of morphisms in ${\cal M}$, with composition of morphisms done componentwise. So, when we say that the tensor product is a functor $\otimes \colon {\cal M}\times {\cal M}\rightarrow {\cal M}$, this implies that for any pair of objects $x,y \in {\cal M}$ there is an object $x \otimes y \in {\cal M}$, while for any pair of morphisms $f \colon x \rightarrow x', g \colon y \rightarrow y'$ in ${\cal M}$ there is a morphism $f \otimes g \colon x \otimes y \rightarrow x' \otimes y'$ in ${\cal M}$. Morphisms are just as important as objects! For example, in ${\rm Hilb}$, not only can we take the tensor product of Hilbert spaces, but also we can take the tensor product of bounded linear operators $S \colon H \rightarrow H'$ and $T \colon K \rightarrow K'$, obtaining a bounded linear operator

$$S \otimes T \colon H \otimes K \rightarrow H' \otimes K'.$$

In physics, we think of $S \otimes T$ as a joint process built from the processes $S$ and $T$ `running in parallel'. For example, if we have a joint quantum system whose two parts evolve in time without interacting, any time evolution operator for the whole system is given by the tensor product of time evolution operators for the two parts.

Figure 8: Two cobordisms and their tensor product

Similarly, in $n{\rm Cob}$ the tensor product is given by disjoint union, both for objects and for morphisms. In Figure 8 we show two spacetimes $M$ and $M'$ and their tensor product $M \otimes M'$. This as a way of letting two spacetimes `run in parallel', like independently evolving separate universes. The resemblance to the tensor product of morphisms in ${\rm Hilb}$ should be clear. Just as in ${\rm Hilb}$, the tensor product in $n{\rm Cob}$ is not a cartesian product: there are no projections with the required properties. There is also no natural choice of a cobordism from $S$ to $S \otimes S$. This means that the very nature of topology prevents us from finding spacetimes that `discard' part of space, or `duplicate' space. Seen in this light, the fact that we cannot discard or duplicate information in quantum theory is not a flaw or peculiarity of this theory. It is a further reflection of the deep structural analogy between quantum theory and the conception of spacetime embodied in general relativity.

Turning to clause (iii) in the definition, we see that a monoidal category needs to have a `unit object' $I$. This serves as the multiplicative identity for the tensor product, at least up to isomorphism: as we shall see in the next clause, $I \otimes A \cong A$ and $A \otimes I \cong A$ for every object $A \in {\cal M}$. In ${\rm Hilb}$ the unit object is ${\mathbb{C}}$ regarded as a Hilbert space, while in $n{\rm Cob}$ it is the empty set regarded as an $(n-1)$-dimensional manifold. Any category with finite products gives a monoidal category in which the unit object is the terminal object $1$.

This raises an interesting point of comparison. In classical physics we describe systems using objects in a category with finite products, and a state of the system corresponding to the object $A$ is just a morphism $f \colon 1 \rightarrow A$. In quantum physics we describe systems using Hilbert spaces. Is a state of the system corresponding to the Hilbert space $H$ the same as a bounded linear operator $T \colon {\mathbb{C}}\rightarrow H$? Almost, but not quite! As we saw in Section 3, such operators are in one-to-one correspondence with vectors in $H$: any vector $\psi \in H$ corresponds to an operator $T_\psi \colon {\mathbb{C}}\rightarrow H$ with $T_\psi(1) = \psi$. States, on the other hand, are the same as unit vectors modulo phase. Any nonzero vector in $H$ gives a state after we normalize it, but different vectors can give the same state, and the zero vector does not give a state at all. So, quantum physics is really different from classical physics in this way: we cannot define states as morphisms from the unit object. Nonetheless, we have seen that the morphisms $T \colon {\mathbb{C}}\rightarrow H$ play a fundamental role in quantum theory: they are just Dirac's `kets'.

Next, let us ponder clause (iv) of the definition of monoidal category. Here we see that the tensor product is associative, but only up to a specified isomorphism, called the `associator'. For example, in ${\rm Hilb}$ we do not have $(H \otimes K) \otimes L = H \otimes (K \otimes L)$, but there is an obvious isomorphism

$$a_{H,K,L} \colon (H \otimes K) \otimes L \rightarrow H \otimes (K \otimes L)$$

given by

$$a_{H,K,L} ((\psi \otimes \phi) \otimes \eta) = \psi \otimes (\phi \otimes \eta) .$$

Similarly, we do not have ${\mathbb{C}}\otimes H = H$ and $H \otimes {\mathbb{C}}= H$, but there are obvious isomorphisms

$$\ell_H \colon {\mathbb{C}}\otimes H \rightarrow H, \qquad r_H \colon H \otimes {\mathbb{C}}\rightarrow H .$$

Moreover, all these isomorphisms are `natural' in a precise sense. For example, when we say the associator is natural, we mean that for any bounded linear operators $S \colon H \rightarrow H'$, $T \colon K \rightarrow K'$, $U \colon L \rightarrow L'$ the following square diagram commutes:

$$\xymatrix{ (H \otimes K) \otimes L \ar[rr]^{a_{H,K,L}} \a... ...mes L' \ar[rr]^{a_{H',K',L'}} && H' \otimes (K' \otimes L') }$$

In other words, composing the top morphism with the right-hand one gives the same result as composing the left-hand one with the bottom one. This compatibility condition expresses the fact that no arbitrary choices are required to define the associator: in particular, it is defined in a basis-independent manner. Similar but simpler `naturality squares' must commute for the left and right unit laws.

Finally, what about clauses (v) and (vi) in the definition of monoidal category? These are so-called `coherence laws', which let us manipulate isomorphisms with the same ease as if they were equations. Repeated use of the associator lets us construct an isomorphism from any parenthesization of a tensor product of objects to any other parenthesization -- for example, from $((A \otimes B) \otimes C) \otimes D$ to $A \otimes (B \otimes (C \otimes D))$. However, we can actually construct many such isomorphisms -- and in this example, the pentagonal diagram in clause (v) shows two. We would like to be sure that all such isomorphisms from one parenthesization to another are equal. In his fundamental paper on monoidal categories, Mac Lane [23] showed that the commuting pentagon in clause (v) guarantees this, not just for a tensor product of four objects, but for arbitrarily many. He also showed that clause (vi) gives a similar guarantee for isomorphisms constructed using the left and right unit laws.

© 2004 John Baez
baez@math.removethis.ucr.andthis.edu

home