


|
|

|
In Part 1 and Part 2 we looked at the delightful curves you get by rolling one circle on another. Now let's see what happens when you roll one circle inside another!
If you roll a circle inside a circle that's 4 times as big, we get an astroid:
Puzzle 1. How many times does the rolling circle turn as it rolls all the way around?
By the way: don't confuse an astroid with an asteroid. They both got their names because someone thought they looked like stars, but that's where resemblance ends!
You can get an astroid using this funny parody of the equation for a circle:
$$ x^{2/3} + y^{2/3} = 1$$
Or, if you don't like equations, you can get a quarter of an astroid by letting a ladder slide down a wall and taking a time-lapse photo!
In other words, you get a whole astroid by taking the envelope of all line segments of length 1 going from some point on the x axis to some point on the y axis!
If the fixed circle is just 3 times as big as the one rolling inside it, we get an deltoid:
Puzzle 2. Now how many times does the rolling circle turn as it rolls all the way around?
By the way: it looks like we're back to naming curves after body parts... but we're not: both this curve and the muscle called a deltoid got their names because they look like the Greek letter delta:

Puzzle 3. Did the Greek letter delta get that name because it was shaped like a river delta, or was it the other way around?
As you might almost expect by now, if you've been reading this whole series, there are weird relations between the deltoid and the astroid.
For example: take a deltoid and shine parallel rays of light at it from any direction. Then the envelope of these rays is an astroid!
We summarize this by saying that the astroid is a catacaustic of the deltoid. This picture is by Xah Lee, who has also made a nice movie of what happens as you rotate the light source:
• Xah Lee, Deltoid catacaustic movie.
I don't completelly understand the rays going through the deltoid, in either the picture or the movie. It looks like those rays are getting refracted, but that would be a diacaustic, not a catacaustic. I think they're formed by continuing reflected rays to straight lines that go through the deltoid. If you didn't do that you wouldn't get a whole astroid, just part of one.
Anyway, at the very least you get part of an astroid, which you can complete to a whole one. And then, as you rotate the light source, the astroid you get rolls around the deltoid in a pleasant manner! This is nicely illustrated here:
• Deltoid catacaustic, Wolfram Mathworld.
You can also get a deltoid from a deltoid! Draw all the osculating circles of the deltoid—that is, circles that match the deltoid's curvature as well as its slope at the points they touch. The centers of these circles lie on another, larger deltoid:
We summarize this by saying that the evolute of a deltoid is another deltoid.
There are also fancier ways to get deltoids if you know more math. For example, the set of traces of matrices lying in the group SU(3) forms a filled-in deltoid in the complex plane!
This raises an interesting question:
Puzzle 4. Is the set of traces of matrices lying in SU(4) a filled-in astroid? In simpler terms, consider the values of \( a + b + c + d \) that we can get from complex numbers \( a,b,c,d\) with \( |a| = |b| = |c| = |d| = 1\) and \( abcd = 1. \) Do these values form a filled-in astroid?
For the answer, go to the last section of this article.
But now comes the climax of today's story: what happens when we let a circle roll inside a circle that's exactly twice as big?
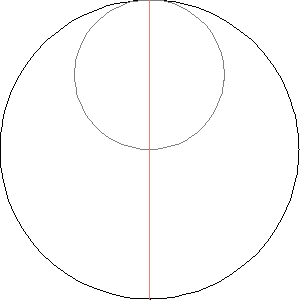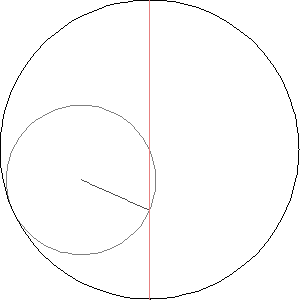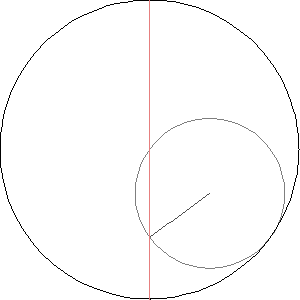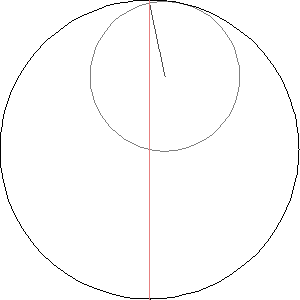
Now you can see the rolling circle turn around once as it rolls all the way around the big one.
More excitingly, if we track a point on the rolling circle, it traces out a straight line! Can you see why? Later I'll give a few proofs.
This gadget is called a Tusi couple. You could use it to convert a rolling motion into a vibrating one using some gears. Greg Egan made a nice animation showing how:

The Tusi couple is named after the Persian astronomer and mathematician Nasir al-Din al-Tusi, who discovered it around 1247, when he wrote a commentary on Ptomely's Almagest, an important astronomical text:
He wrote:
If two coplanar circles, the diameter of one of which is equal to half the diameter of the other, are taken to be internally tangent at a point, and if a point is taken on the smaller circle—and let it be at the point of tangency—and if the two circles move with simple motions in opposite direction in such a way that the motion of the smaller is twice that of the larger so the smaller completes two rotations for each rotation of the larger, then that point will be seen to move on the diameter of the larger circle that initially passes through the point of tangency, oscillating between the endpoints.
I don't quite understand why he was interested in this, but it has something to do with using epicycles to build linear motion out of circular motion. It also has something to do with the apparent motion of planets between the Earth and the Sun.
Later Copernicus also studied the Tusi couple. He proved that the moving point really did trace out a straight line:
However, many suspect that this was not a true rediscovery: al-Tusi had also proved this, and some aspects of Copernicus' proof seem too similar to al-Tusi's to be coincidence:
• George Saaliba, Whose science is Arabic science in Renaissance Europe?, Section 2: Arabic/Islamic science and the Renaissance science in Italy.
• I. N. Veselovsky, Copernicus and Nasir al-Din al-Tusi, Journal for the History of Astronomy 4 (1973), 128–130.
In fact, the Tusi couple goes back way before al-Tusi. It was known to Proclus back around 450 AD! Apparently he wrote about it in his Commentary on the First Book of Euclid. Proclus is mainly famous as a philosopher: people think of him as bringing neo-Platonism to its most refined heights. Given that, it's no surprise that he also liked math. Indeed, he said:
Wherever there is number, there is beauty.
And of course this is what I've been trying to show you throughout this series.
So, here are three proofs that a Tusi couple really does trace out a straight line. I posed this as a puzzle on Google+, and here are my favorite three answers. I like them because they're very different. Since people have thought about Tusi couples since 450 AD, I doubt any of these proofs are original to the people I'm mentioning here! Still, they deserve credit.
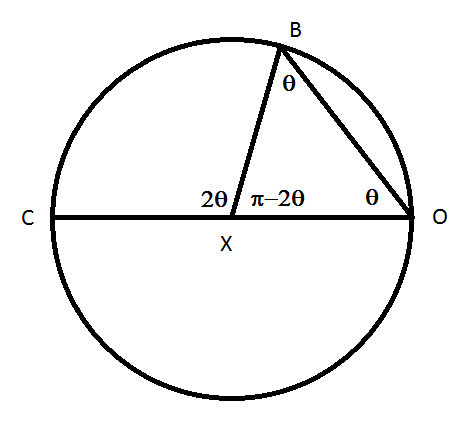
The first, due to Omar Antolín Camarena, is in the style of traditional Euclidean geometry.
Let O be the center of the big circle. Let A be the position of the traced point at the instant t when it's the point of tangency between the circles, let B be its position at some future time t. and let C be the point of tangency at that same time t.. Let X be the center of the small circle at that future time t..

We want to prove A, B and O lie on a line. To do this, it suffices to show that the angle AOC equals the angle BOC:
Want: ∠BOC = ∠AOC
The arc AC of the big circle has the same length as the arc BC of the small circle, since they are both the distance rolled between times t and t.. But the big circle is twice as, so the angle BXC on the little circle must be twice the angle AOC on the big circle:
Know: ∠BXC = 2 ∠AOC
But it's a famous fact in Euclidean geometry that the angle BXC is twice the angle BOC:
Know: ∠BXC = 2 ∠BOC
From the two equations we know, the one we want follows!
Here's the proof of that 'famous fact', in case you forgot it:
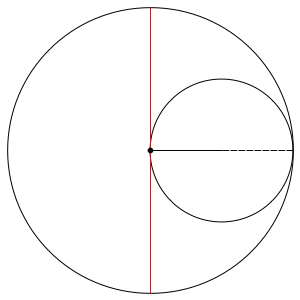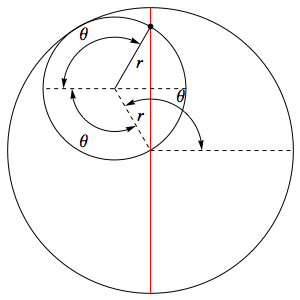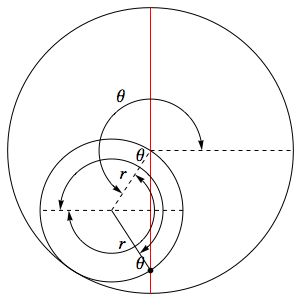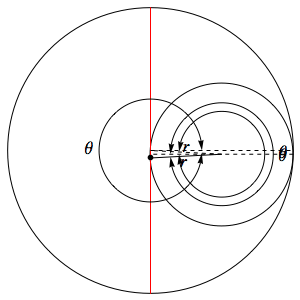
It's a 'proof without words', so you may need to think a while to see how it shows that the Tusi couple traces out a straight line.
The third proof is due to Boris Borcic. It uses complex numbers. Let the big circle be the unit circle in the complex plane. Then the point of contact between the rolling circle and the big one is:
$$ e^{i t}$$
so the center of the rolling circle is:
$$ \displaystyle{ \frac{e^{it}}{2} } $$
Since the rolling circle turns around once clockwise as it rolls around the big one, the point whose motion we're tracking here:

is equal to:
$$ \displaystyle{ \frac{e^{it}}{2} + \frac{e^{i(\pi - t)}}{2} = \frac{e^{i t} - e^{-i t}}{2} = i \sin t = i \; \mathrm{Im}(e^{it}) } $$
So, this point moves up and down along a vertical line, and its height equals the height of the point of contact, \( e^{it}.\)
But the same sort of argument shows that if we track the motion of the opposite point on the rolling circle, it equals:
$$ \displaystyle{ \frac{e^{it}}{2} - \frac{e^{i(\pi - t)}}{2} = \frac{e^{i t} + e^{-i t}}{2} = \cos t = \mathrm{Re}(e^{it}) } $$
So, this opposite point moves back and forth along a horizontal straight line... and its horizontal coordinate equals that of the point of contact!
You can see all this clearly in the animation Borcic made:
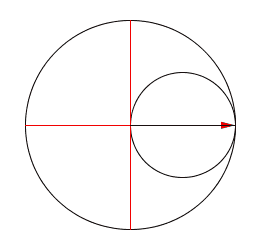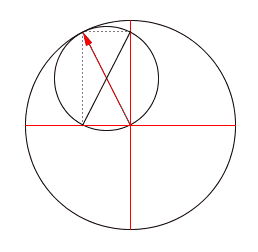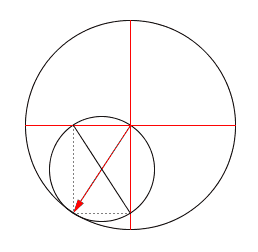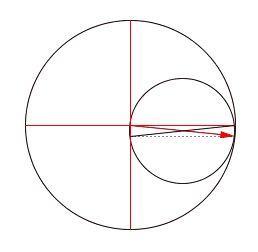
The point of contact, the tip of red arrowhead, is \(e^{it}\). The two opposite points on the rolling circle are \( \cos t \) and \( i \sin t\). So, the rectangle here illustrates the fact that
$$ e^{it} = \cos t + i \sin t $$
It's interesting that this famous formula is hiding in the math of the Tusi couple! But it shouldn't be surprising, because the Tusi couple is all about building linear motion out of circular motion... or conversely, decomposing a circular motion into linear motions.
Is the set of traces of matrices lying in SU(4) a filled-in astroid? In simpler terms, consider the values of \( a + b + c + d \) that we can get from complex numbers \( a,b,c,d\) with \( |a| = |b| = |c| = |d| = 1\) and \( abcd = 1. \) Do these values form a filled-in astroid?
Greg Egan, Shanthanu Bhardwaj and Aaron Wolbach figured out the answer: yes!
And the pattern continues. The hypocycloid with \(n\) cusps is the curve formed by rolling a circle inside a circle whose radius is \(n\) times larger. And it turns out that the set of traces of matrices lying in \( \mathrm{SU}(n)\) is always a filled-in hypocycloid with \(n\) cusps!
This pattern has a wonderful consequence:
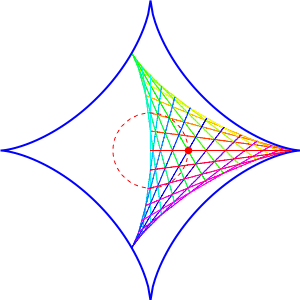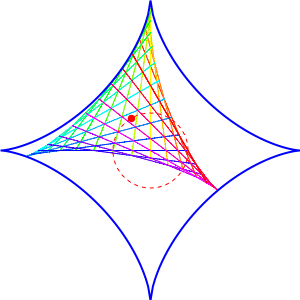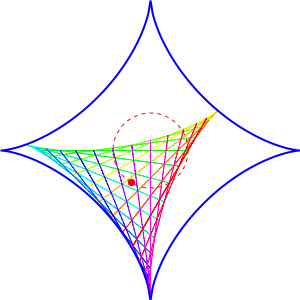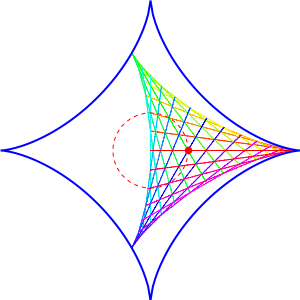
The picture here, created by Greg Egan, shows a deltoid rolling inside an astroid. Note that it fits in a perfectly snug way! More generally, a hypocycloid with \(n\) cusps always rolls snugly inside a hypocycloid with \(n+1\) cusps.
Let's see why. At this point the math gets harder, so you may want to skip down to the pictures if you're not keen on proofs.
If you have a matrix in \(\mathrm{SU}(n+1)\), its \(n+1\) eigenvalues can be any unit complex numbers that multiply to 1, and its trace is the sum of these numbers. We can take \(n\) of them to be \(e^{i \theta}\), and then the remaining one has to be \(e^{-i n \theta}\). Then their sum is $$ n e^{i \theta} + e^{-i n \theta} $$ But this is also the curve traced out by a small circle of radius 1 rolling inside a big circle of radius \(n+1\). Why? As it rolls, the small circle's center moves around a circle of radius \(n\), tracing out the curve \(n e^{i \theta}\). But as it rolls, the small circle turns in the opposite direction at an angular velocity that's \(n\) times higher. This gives the term \(e^{-i n \theta}\).
In short, we have seen that $$ H_{n+1} = \{ n e^{i \theta} + e^{-i n \theta} : 0 \le \theta \le 2 \pi \} $$ is a hypocycloid with \(n+1\) cusps, and if we define $$\mathrm{tr}(\mathrm{SU}(n+1)) = \{ \mathrm{tr}(g) : g \in \mathrm{SU}(n+1) \} $$ then $$ H_{n+1} \subseteq \mathrm{tr}(\mathrm{SU}(n+1)) $$
In fact, the hypocycloid \(H_{n+1}\) is precisely the boundary of \(\mathrm{tr}(\mathrm{SU}(n+1))\). To show this, note that the eigenvalues of any element of \(\mathrm{SU}(n+1)\) can be written as $$ e^{i\phi_1} , \; \dots, \; e^{i\phi_{n}} , \; e^{-i(\phi_1+\phi_2+ \cdots +\phi_{n})} $$ so its trace is $$ e^{i\phi_1} + \cdots + e^{i\phi_{n}} + e^{-i(\phi_1+\phi_2+ \cdots +\phi_{n})} $$ where the angles \(\phi_i\) are arbitrary. When all the \(\phi_i\) equal the same angle \(\theta\), the trace gives a point in the hypocycloid \(H_{n+1}\). But if we compute the derivative of the trace with respect to any angle \(\phi_i\) at a point where they.re all equal, the derivative is always tangent to this hypocycloid: it's just \(\frac{1}{n-1}\) times the derivative of $$ n e^{i \theta} + e^{-i n \theta}$$ with respect to \(\theta\). Except at the cusps, some neighborhood of the tangent line lies in the interior of the filled hypocycloid, so no change in the \(\phi_i\) can take you out of it. And at the cusps, moving along the tangent out of the hypocycloid would take you out of the disk of radius \(n\), which is forbidden by the triangle inequality.
Furthermore, any point inside the hypocycloid \(H_{n+1}\) is an element of \(\mathrm{tr}(\mathrm{SU}(n+1))\). To see this, note that \(\mathrm{SU}(n+1)\) is simply connected, and thus so is its image under the continuous map $$ \mathrm{tr} \colon \mathrm{SU}(n+1) \to \mathbb{C} $$ Since its image includes the hypocycloid \(H_{n+1}\), which bounds a set homeomorphic to a disk, its image must include this whole set. (Here we use a fact from topology, that a subset of a disk containing the boundary but missing some point in the interior cannot be simply connected.)
In summary, \(\mathrm{tr}(\mathrm{SU}(n+1))\) is precisely the closed set in the plane bounded by hypocycloid \(H_{n+1}\). We can use this to see that a hypocycloid with \(n\) cusps rolls snugly inside a hypocycloid with \(n+1\) cusps. Recall that the eigenvalues of a matrix in \(\mathrm{SU}(n)\) are of the form $$ e^{i\phi_1}, \; \dots , \; e^{i\phi_{n-1}}, \; e^{-i(\phi_1+\phi_2+...+\phi_{n-1})} $$ where the angles \(\phi_i\) are arbitrary. On the other hand, the eigenvalues of any element of \(\mathrm{SU}(n+1)\) can be written as $$ e^{i\theta}e^{i\phi_1}, \; \dots , \; e^{i\theta}e^{i\phi_{n-1}}, \;e^{i\theta}e^{-i(\phi_1+\phi_2+...+\phi_{n-1})}, e^{-in\theta} $$ where the angles \(\phi_i\) and \(\theta\) are arbitrary. Thus we have $$ \mathrm{tr}(\mathrm{SU}(n+1)) = \bigcup_{0 \le \theta \le \pi} e^{i\theta} \mathrm{tr}(\mathrm{SU}(n)) + e^{-in\theta} $$ And as \(\theta\) ranges from \(0\) to \(2\pi\), this gives a filled-in hypocycloid with \(n\) cusps rolling snugly inside one with \(n+1\) cusps!
Egan's picture above illustrates the case \(n = 2\). The circling red dot shows what happens as \(\theta\) changes. Each of the colored lines shows what happens when we vary \(\phi_1\), while the progression from line to line sweeping out a filled-in deltoid is due to varying \(\phi_2\).
Here's the case \(n = 3\), also drawn by Greg Egan:
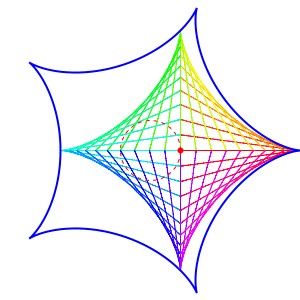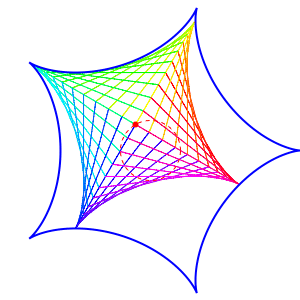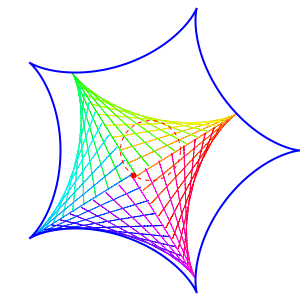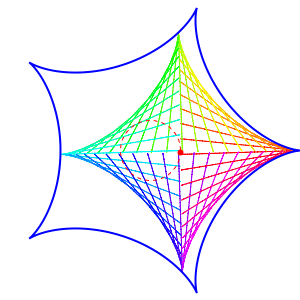
Not all this math is new; it was already discussed here:
Here is his picture for \(\mathrm{SU}(6)\), which gives a hypocycloid with 6 cusps:
He also considers traces for groups other than \(SU(n)\). It's neat how the traces of \(\mathrm{Spin}(4n+2)\) elements in the spinor representation lie in a curve a bit like an astroid, but which gets skinnier and skinnier as \(n\) increases:
It's also neat how \(\mathrm{E}_6\) in one of its two complex 27-dimensional reps gives traces lying in a curve a bit like a deltoid, but skinnier:
Few of these pictures were made by me, and none of the animations. For most, you can see who created them by clicking on them. The animation of the astroid and deltoid as envelopes come from here:
• Envelope, Math Images Project.
where they were made available under a GNU Free Documentation License. Here's another animation from there:
This is a way of creating a deltoid as the envelope of some lines called 'Wallace-Simson lines'. The definition of these lines is so baroque I didn't dare tell it to you it earlier. But if you're so bored you're actually reading these credits, you might enjoy this.
Any triangle can be circumscribed by a circle. If we take any point on this circle, say M, we can drop perpendicular lines from it to the triangle's three sides, and get three points, say P, Q and R:
Amazingly, these points lie on a line:
This is the Wallace–Simson line of M. If we move the point M around the circle, we get lots of Wallace–Simson lines... and the envelope of these lines is a deltoid!
By the way: the Wallace–Simson line is named after William Wallace, who wrote about it, and Robert Simson, who didn't. Don't confuse it with the Wallace line! That was discovered by Alfred Russel Wallace.
You can see answers to the puzzles on Azimuth, and make your own comments or ask questions there!

|
|

|