 |
I will begin with a thoroughly fictionalized account of the quest in physics to find bigger and bigger symmetry groups. Then I will say a bit about how that quest has led to some interesting applications of category theory.
Once upon a time up was up, down was down, so the symmetry group of the world was E(2), the Euclidean group in two dimensions. This is a 3-dimensional group since it is generated by:
In classical physics - or to be precise, "Hamiltonian mechanics" or "Lagrangian mechanics" - each symmetry of the laws of physics gives rise to a conserved quantity. This is a wonderful result called Noether's theorem. From the translational symmetries we get conservation of momentum in the x, y, and z directions, while from the rotational symmetries we get angular momentum in the xy, xz, and yz planes.
The laws of physics are also invariant under time evolution itself. Time evolution is a symmetry of spacetime given by
t → t + c
x → x
y → y
z → z
and the corresponding conserved quantity is energy. Ultimately, this is because energy tells you how fast things are wiggling around as time passes!
The group consisting of E(3) plus time evolution (i.e. the direct sum E(3)+R) doesn't have any common name, but it's the simplest group of spacetime symmetries. Simplest in the sense of most naive, that is.
Galileo pointed out that the laws of physics are the same in a boat moving on a constant speed (at least on a calm sea!). This gives rise to the notion of Galilei transformations:
t → t
x → x + vt
y → y
z → z
(and similarly for y and z) which express how to transform coordinates into a frame of reference moving at velocity v in the x direction. The Galilei group is a group containing E(3)+R but also these:
Thus this group, sometimes called G (a fancy script G, please!) is 10-dimensional. This is the group of symmetries of classical mechanics.
Maxwell's equations, alas, were not symmetric under the group G! How could they be: they say that light moves at the same speed - let's call it "1" - no matter what unaccelerated frame of reference one is in! This is inconsistent with how velocities transform under the Galilei transformations.
Poincaré realized that the symmetry group of Maxwell's equations was (at least) the Poincaré group. "My group!" he cried, "Amazing - the laws of nature just happen to be symmetric under a group named after me!"
His group is just like the Galilei group except that the formula for the Galilei transformations gets changed to the following "Lorentz transformations":
t → (cosh s)t + (sinh s)x
x → (sinh s)t + (cosh s)x
y → y
z → z
(and similar ones for y and z). These express how one transforms coordinates into a different unaccelerated coordinate system in special relativity. Here s, the "rapidity", is related to the ordinary velocity v by v = tanh s. Note that this means |v| is less than 1 for real rapidities - the speed limit is 1!
Here, of course, I'm working in units where the speed of light is 1. People only started using such units after they realized that Lorentz transformations mixed up space and time. Before that, people foolishly used different units for space and time - like "meters" and "seconds" - which gave the false impression that the speed of light was actually an interesting physical constant. It's a bit like how the Egyptians, when building pyramids, used to measure horizontal distances in "palms" and vertical distances in "cubits". Seven palms per cubit - did they think this was an interesting physical constant? (Thanks go to Michael Weiss for digging this fact out of Eli Maor's book Trigonometric Delights.)
The formula for the Lorentz tranformations looks awfully like the formula for rotations:
t → t
x → (cos θ)x + (sin θ)y
y → -(sin θ)x + (cos θ)y
z → z
except that the trig functions have been replaced by hyperbolic trig functions and that ugly minus sign is gone! I won't explain why, but any decent physicist can.
In any event, the Poincaré group is 10 dimensional like the Galilei group. What, one may ask, are the conserved quantities corresponding to the Lorentz transformations? This is a good riddle to test undergraduates. If you get stuck, go here.
But Maxwell's equations have even more symmetries than those in the Poincaré group. The reason is that these equations have have no characteristic length scale. In other words, anything you can make out of light, you can make a replica of that is just a scaled-up or scaled-down version. Thus in addition to the Poincare group Maxwell's equations are invariant under scale transformations, or "dilations":
t → ct
x → cx
y → cy
z → cz
The group consisting of the Poincaré group and dilations is sometimes called the "Weyl group". (Beware: mathematicians also call a different sort of group a Weyl group.) The Weyl group is 11-dimensional.
Only massless particles are invariant under the Weyl group. A mass sets a length scale. Huh? To see this one needs to use relativity and quantum mechanics. Mass has dimensions of M. Length has dimension L. In relativity we have a constant, the speed of light, with dimensions L/T, and in quantum mechanics we have a constant, Planck's constant, with dimensions ML2/T = energy × time = momentum × position. These two constants enable us to trade units of mass for dimensions of inverse length. In other words:
M = (ML2/T)(T/L)1/L = hbar/c 1/L.
In nature it appears that the only massless particles are the photon and the (hypothesized) graviton. The neutrinos aren't very heavy, but these days it's looking more and more like they do have a nonzero mass.
Now massless particles are in fact symmetric under an even bigger group than the Lorentz group - namely, the conformal group. This group doesn't act as symmetries of Minkowski spacetime, but under a (mathematically useful) completion, the "conformal compactification of Minkowski space". This group is 15-dimensional and it's just the group SO(2,4), or if you prefer, the covering group SU(2,2)! I have used this group a lot in my study of nonlinear partial differential equations. Maxwell's equations are invariant under the conformal group but there aren't too many other equations that are. The massless Dirac equation is one - that's for the neutrinos. There are other linear equations for free particles of any spin. There are not too many nonlinear equations invariant under the conformal group but there is a very famous one - the Yang-Mills equations. These of course are used to describe the weak and strong interactions. (In practice various sneaky things - infrared slavery and Higgses - conspire to cloak the conformal invariance of the fields in these cases, so the practical relevance of conformal symmetry is limited.) There also is a nice baby version of the Yang-Mills equations, namely the massless phi4 theory. I spent a bunch of time studying these 2 equations using conformal symmetry. Here one uses the amazing fact that in conformally invariant theories one can define an alternate notion of energy coming from an alternate "time evolution" symmetry contained in the conformal group - the "Einstein energy".
Now I should point out that for each of the symmetry groups I've listed above, people have worked out the "representations" of these groups. A representation of a group is a way to think of its elements as operators, and this is what we need to understand symmetries in quantum physics. The representation theory of the Poincar´ group dominates relativistic physics, while the representation theory of the Galilei group dominates nonrelativistic physics. I encourage everyone to learn the derivation of Schrödinger's equation straight from the representation theory of the Galilei group! It's cool. (I think it appears in the books by Mackey and Jauch listed here.)
In any event, we can ask for still more symmetry than conformal symmetry. We can ask for symmetry under all smooth coordinate transformations! The first to demand this effectively was Einstein, who got his wishes when he devised general relativity as a theory of gravity. So gravity is the most symmetrical of field theories so far - it's "generally covariant", or invariant under the group Diff(M) all diffeomorphisms of a spacetime M! One can also come up with a (classical) theory of gravity coupled to Yang-Mills fields, or whatever fields you like.
In these theories one may ask what sort of quantity we get associated to the symmetries under all smooth coordinate transformations. We get exactly the stress-energy tensor, which is a symmetric 2-tensor field whose divergence is zero. This is what becomes of conservation of energy and momentum in general relativity. There is generally no conserved "total energy of the universe" or "total momentum", since there is no canonical choice of time or space translations in a wiggly spacetime. There is only a divergence-free stress-energy tensor - which is actually nicer since it expresses the locality of the notion of energy and momentum.
Okay, is that enough symmetry yet? Well, there can be a lot more! But we're in trouble already, because curiously it is the extremely high degree of symmetry of general relativity that has made it hard to quantize gravity. That seems odd - that too much symmetry could make a problem hard! The point is that we don't know how to use so much symmetry. We are not used to the fact that in quantizing gravity there is no "background metric" with which to establish the relative positions of points. All the techniques of physics (n-point Greens functions, Hamiltonians) are adapted to a situation in which you can measure times and distances with respect to a fixed metric, not a metric that can wiggle around in many ways and is one of the fields one is trying to quantize! Moreover, the representation theory of diffeomorphism groups is hard and still poorly understood in 4 dimensions. Plus, it's not clear that the representations of the diffeomorphism group are all that relevant... unlike the previous groups, the diffeomorphism group is often regarded as a "gauge" group, that is, a group expressing the fact that the mathematics you have used to express the physics contains redundancies - i.e., two spacetimes with metrics that are equivalent under some diffeomorphism should really be regarded as the same physical system. So to get to the real physics one should simply mod out by the diffeomorphsim group. That's what people often say, anyway - this is a somewhat controversial and confused subject.
In any event, a quantum field theory that is invariant under all diffeomorphisms of spacetime is called by physicists a "topological quantum field theory," or TQFT. It has only been a few years since people have been seriously studying worked-out examples of TQFTs. The understandable examples so far have been in 2- and 3-dimensional spacetimes, not our own lovely 4-dimensional spacetime. But these examples are still amusing and perhaps enlightening. They also have a lot to do with knots - but that's another story.
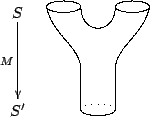
What's a topological quantum field theory, mathematically? It's a functor. Namely, it is a functor from the category Cob to the category Hilbert. The category Cob is the category whose objects are (n-1)-dimensional manifolds ("space") and whose morphisms are n-dimensional manifolds ("spacetime") having one (n-1)-dimensional manifold as "incoming" and another as "outgoing" boundary. We say that the n-manifold is a cobordism between the two (n-1)-manifolds. For example, in n = 2, the "trinion" or "pair of pants" is a cobordism M from a space S consisting of two circles to a space S' consisting of one:
 |
In any event, a TQFT is a "functor" from the cobordism category nCob (for some dimension n) to the category Hilb of Hilbert spaces. That is, a TQFT assigns to each (n-1)-dimensional manifold S a Hilbert space of states Z(S). This Hilbert space desscribe all the the states our theory has when space is the manifold S. Also, a TQFT assigns to any cobordism
M: S → S'
between such manifolds an operator
Z(S): Z(S) → Z(S').
This operator describes time evolution: how states on S turn into states on S'. Since there is no such thing as waiting "a certain amount of time" in a general TQFT, this time evolution operator only depends on the topology of the cobordism S. That's why it's called a topological quantum field theory!
People have worked out interesting examples of TQFT's for n = 2 and n = 3, the latter being more interesting since 3-dimensional manifolds are quite sneaky. The most famous 3-dimensional TQFT is Chern-Simons theory. I won't explain this now, but simply attempt to lure the reader into studying it by noting:
Here is a beautiful related result. Say one is in the vacuum and has two linked loops. Let E denote the integral of the electric field through the surface spanned by one loop, and let B denote the integral of the magnetic field through the surface spanned by the other. One can use quantum electrodynamics to show that
ΔE ΔB ≥ (hbar/2) L
where L is the linking number of the two loops! Thus the canonical commutation relations for E and B in this form are diffeomorphism-invariant - which is curious because quantum electrodynamics is not! I think this result is due to Ashtekar and Corichi.
The last part is the most exciting to me, since it says that not only are TQFT's mathematically interesting, they may also shed light on real-world physics, namely, quantum gravity. It's a long story that's not completely understood yet by any means!
Note that a TQFT is a "representation of a category," that is, a functor from some category to a category of vector spaces (or Hilbert spaces). Thus, the concept of symmetry in topological quantum field theories generalize that in earlier theories. Earlier theories only dealt with group representations, while TQFTs are category representations!
So, in modern physics categories are gradually beginning to take over where groups left off, expanding our concept of symmetry. To understand how this actually works, you should probably bone up a bit on categories, and then check out my website on Higher-dimensional algebra and Planck-scale physics.