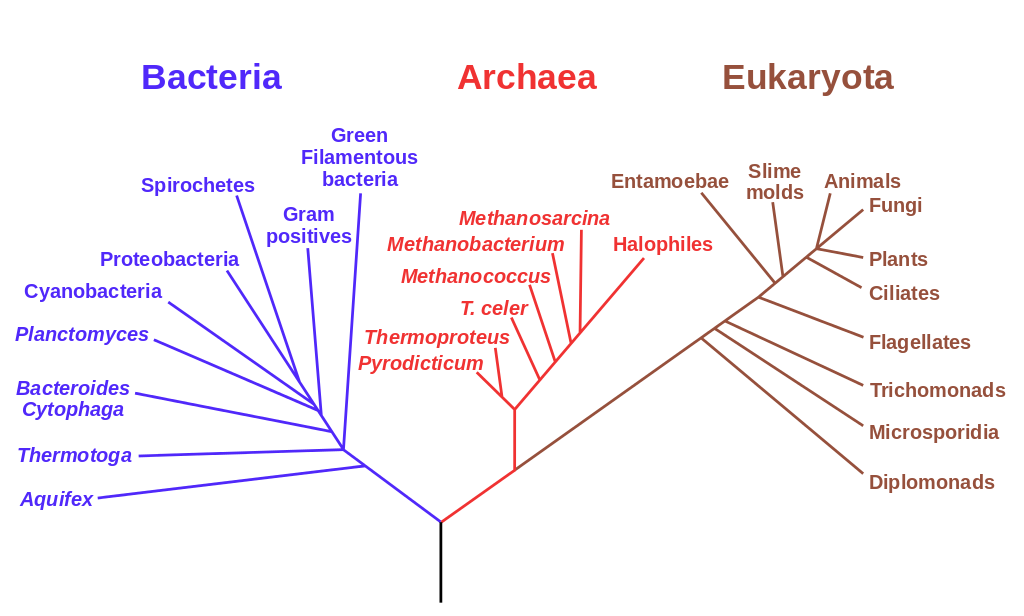

Trees are not just combinatorial structures: they are also biological structures, both in the obvious way but also in the study of evolution. Starting from DNA samples from living species, biologists use increasingly sophisticated mathematical techniques to reconstruct the most likely 'phylogenetic tree' describing how these species evolved from earlier ones. In their work on this subject, they have encountered an interesting example of an operad, which is obtained by applying a variant of the Boardmann–Vogt 'W construction' to the operad for commutative monoids. The operations in this operad are labelled trees of a certain sort, and it plays a universal role in the study of stochastic processes that involve branching. It also shows up in tropical algebra. This talk is based on work in progress with Nina Otter.
You can see the slides here. For more discussion, see my paper with Nina: