




|
 
|

|
This week I want to mention a couple of papers lying on the interface of physics, topology, and higher-dimensional algebra. But first, some astronomy pictures... and a bit about the mathematical physicist Hamilton!
I like this photo of a jet emanating from the black hole in the center of galaxy M87:
1) NASA and John Biretta, M87, http://hubblesite.org/newscenter/newsdesk/archive/releases/2005/12/image/o
M87 is a giant elliptical galaxy. It's long been known as a powerful radio source, and now we know why: there's a supermassive black hole in the center, about 3 billion times the mass of our Sun. As matter spirals into this huge black hole, it forms an "accretion disk", and some gets so hot that it shoots out in a jet, as envisioned here:
2) NASA, MAXIM: Micro-Arcsecond X-ray Imaging Mission, http://maxim.gsfc.nasa.gov/docs/science/science.html
Accretion disks and jets are common at many different scales in our universe. They're just nature's way of letting a bunch of matter fall in under its own gravitation while losing angular momentum and energy. We see them when dust clouds collapse to form stars, we see them when black holes sucks in mass from companion stars, and they're probably also responsible for slow γ ray bursts as huge stars collapse when they run out of fuel - see "week204" for that story.
But, among the biggest accretion disks and jets are those surrounding supermassive black holes in the middle of galaxies. These are probably responsible for all the "active galactic nuclei" or "quasars" that we see. In the case of M87 the jet is enormous: 5000 light years long! To get a sense of the scale, look at the small white specks away from the jet in the next picture. These are globular clusters: clusters containing between ten thousand and a million stars.
3) A jet from galaxy M87, Astronomy Picture of the Day, July 6, 2000, http://antwrp.gsfc.nasa.gov/apod/ap000706.html
The jet in M87 is so hot that it emits not just radio waves and visible light, but even X-rays, as seen by the Chandra X-ray telescope:
4) M87: Chandra sheds light on the knotty problem of the M87 jet, http://chandra.harvard.edu/photo/2001/0134/
It seems the jet consists mainly of electrons moving at relativistic speeds, focused by the magnetic field of the accretion disk. They come in blobs called "knots". People can actually see these blobs moving out, getting brighter and dimmer.
In fact, many galaxies have super-massive black holes at their centers with jets like this one. The special thing about M87 is that it's fairly nearby, hence easy to see. M87 is the biggest galaxy in the Virgo Cluster. This is the closest galaxy cluster to us, about 50 million light years away. That sounds pretty far, but it's only 1000 times the radius of the Milky Way. If the Milky Way were a pebble, M87 would be only a stone's throw away. So, even amateur astronomers - really good ones, at least - can take photos of M87 that show the jet. But here's a high-quality picture produced by Robert Lupton using data from the Sloan Digital Sky Survey - you can see the jet in light blue:
5) Robert Lupton and the Sloan Digital Sky Survey Consortium, The central regions of M87, http://www.astro.princeton.edu/~rhl/PrettyPictures/
Backing off a bit further, let's take a look at the Virgo Cluster. It contains over a thousand galaxies, but we can tell it's fairly new as clusters go, since it consists of a bunch of "subclusters" that haven't merged yet. Our galaxy, and indeed the whole Local Group to which it belongs, is being pulled towards the Virgo Cluster and will eventually join it. Here's a nice closeup of part of the Virgo Cluster:
6) Chris Mihos, Paul Harding, John Feldmeier and Heather Morrison, Deep imaging of the Virgo Cluster, http://burro.astr.cwru.edu/Schmidt/Virgo/
Finally, just for fun, something unrelated - and more mysterious. It's called "Hoag's object":
7) The Hubble Heritage Project, Hoag's Object, http://heritage.stsci.edu/2002/21/
It's a ring-shaped galaxy full of hot young blue stars surrounding a ball of yellower stars. Nobody knows how it formed: perhaps by a collision of two galaxies? Such collisions are fairly common, but they don't typically create this sort of structure.
The weirdest part is that inside the ring, in the upper right, you can see another ring galaxy in the distance! Maybe an advanced civilization over there enjoys this form of art? Probably not, but if it turns out to be true, you heard it here first.
Anyway... back here on Earth, in the summer of 2004, I visited Dublin for a conference on general relativity called GR17. As recounted in "week207", this was where Hawking admitted defeat in his famous bet with John Preskill about information loss due to black hole evaporation. In August of this year, Hawking finally came out with a short paper on the subject:
8) Stephen W. Hawking, Information loss in black holes, available as hep-th/0507171.
I spent a lot of time talking to physicists, but I also wandered around Dublin a bit. Besides listening to some great music at a pub called Cobblestones - Kevin Rowsome plays a mean uilleann pipe! - and tracking down some sites mentioned in James Joyce's novel "Ulysses", I went with Tevian Dray on a pilgrimage to Brougham Bridge.
Tevian Dray is an expert on the octonions, and Brougham Bridge is where Hamilton carved his famous formula defining the quaternions! Now there is a plaque commemorating this event, which reads:
It does't mention that Hamilton had been racking his brain for the entire month of October trying to solve this problem: "flashes of genius" favor the prepared mind. But it's a nice story and a nice place. My friend Tevian Dray took some photos, which you can see here:
9) John Baez, Dublin, http://math.ucr.edu/home/baez/dublin/
It was a bit of a challenge finding Brougham Bridge, since nobody at the main bus station gave us correct information about which bus went there - except the bus driver who finally took us there. So, to ease your way in case you want to make your own pilgrimage, the above page includes directions. And now, thanks to Dirk Schlimm, it also includes a link to a map showing the bridge!
Speaking of Hamilton, Theron Stanford recently sent me an answer to one of life's persistent questions: why is momentum denoted by the letter p?
Since momentum and position play fundamental roles in Hamiltonian mechanics, and they're denoted by p and q, one wonders: could this notation be related to Hamilton's alcoholism in later life? After all, some claim the saying mind your p's and q's began as a friendly Irish warning not to imbibe too many pints and quarts! So, maybe he used these letters in his work on physics as a secret plea for help.
Umm... probably not. Just kidding. But in the absence of hard facts, speculation runs rampant. So, I'm glad Stanford provided some of the former, to squelch the latter.
He sent me this email:
While Googling various subjects, I came across the following from your Quantum Gravity Seminar notes from 2001:So, now the question is why Hamilton chose the letter "varpi":Again Oz was overcome with curiosity, so mimicking Toby's voice, he asked, "Why do we call the momentum p?"Well, I have an answer. Hamilton, the first physicist to actually understand the importance of the concept of momentum, chose π to stand for momentum (actually, it's not the usual π, but what TeX calls varpi, a lower-case ω with a top, kinda like the top of a lower-case τ). Jacobi changed this to p in one of his seminal papers on the subject; he also used q in the same paper to stand for position. In the 1800s (I want to say 1850s, though it might have been a decade or two later) Cayley presented a paper to the Royal Academy in which he says (and I paraphrase), "Well, it seems that p and q are pretty well established now, so that's what I'm going to use."The Wiz glared at Toby. "Because m is already taken -- it stands for mass! Seriously, I don't know why people call position q and momentum p. All I know is that if you use any other letters, people can tell you're not a physicist. So I urge you to follow tradition on this point."
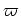
for momentum. This variant of π was fairly common in the mathematical literature of the day, so there may be no special explanation. For some further detective work, see:
10) Hamilton: two mysteries solved, http://groups.google.com/group/sci.physics/browse_thread/thread/d1b7b4a998682bbb/3a868ae8218a4bca#3a868ae8218a4bca
Also see equation 12 in this paper for one of the first uses of "varpi" to mean momentum:
11) William Rowan Hamilton, Second essay on a general method in dynamics, ed. David R. Wilkins, available at http://www.maths.tcd.ie/pub/HistMath/People/Hamilton/Dynamics/SecEssay.pdf
He doesn't say why he chose this letter - it may have been completely random!
Before I turn to higher-dimensional algebra, maybe this is a good time to mention a paper related to the octonions:
12) Jakob Palmkvist, A realization of the Lie algebra associated to a Kantor triple system, available as math.RA/0504544.
In "week193" I mentioned how 3-graded Lie algebras come from "Jordan triple systems", and vaguely hinted that 5-graded Lie algebras come from "Kantor triple systems". I explained how the exceptional Lie algebra E8 gets to be 5-graded, but I didn't really say anything about Kantor triple systems because my understanding of them was so poor. This paper by Palmkvist explains them very clearly! And even better, he shows how the "magic square" Lie algebras F4, E6, E7, and E8 can be systematically obtained from the octonions, bioctonions, quateroctonions and octooctonions by means of Kantor triple systems.
Now for some mathematical physics that touches on higher-dimensional algebra. If you still don't get why topological field theory and n-categories are so cool, read this thesis:
13) Bruce H. Bartlett, Categorical aspects of topological quantum field theories, M.Sc. Thesis, Utrecht University, 2005. Available as math.QA/0512103.
It's a great explanation of the big picture! I can't wait to see what Bartlett does for his Ph.D..
If you're a bit deeper into this stuff, you'll enjoy this:
14) Aaron Lauda and Hendryk Pfeiffer, Open-closed strings: two-dimensional extended TQFTs and Frobenius algebras, available as math.AT/0510664.
This paper gives a purely algebraic description of the topology of open and closed strings, making precise and proving some famous results stated without proof by Moore and Segal, which can be seen here:
15) Greg Moore, Lectures on branes, K-theory and RR charges, Clay Math Institute Lecture Notes (2002), available at http://www.physics.rutgers.edu/~gmoore/clay1/clay1.html
Lauda and Pfeiffer's paper makes heavy use of Frobenius algebras, developing more deeply some of the themes I mentioned in "week174". In a related piece of work, Lauda has figured out how to categorify the concept of a Frobenius algebra, and has applied this to 3d topology:
16) Aaron Lauda, Frobenius algebras and ambidextrous adjunctions, Theory and Applications of Categories 16 (2006) 84-122. Also available as math.CT/0502550.
Aaron Lauda, Frobenius algebras and planar open string topological field theories, available as math.QA/0508349.
The basic idea behind all this work is a "periodic table" of categorified Frobenius algebras, which are related to topology in different dimensions. For example, in "week174" I explained how Frobenius algebras formalize the idea of paint drips on a sheet of rubber. As you move your gaze down a sheet of rubber covered with drips of paint, you'll notice that drips can merge:
\ \ / /
\ \ / /
\ \ / /
\ \ / /
\ \_/ /
\ /
| |
| |
| |
| |
| |
but also split:
| |
| |
| |
| |
| |
/ _ \
/ / \ \
/ / \ \
/ / \ \
/ / \ \
/ / \ \
In addition, drips can start:
_
| |
| |
| |
| |
| |
| |
| |
| |
| |
but also end:
| |
| |
| |
| |
| |
| |
| |
| |
|_|
In a Frobenius algebra, these four pictures correspond to four
operations called "multiplication" (merging),
"comultiplication" (splitting), the "unit"
(starting) and the "counit" (ending). Moreover, these
operations satisfy precisely the relations that you can prove by
warping the piece of rubber and seeing how the pictures change. For
example, there's the associative law:
\ \ / / / / \ \ \ \ / /
\ \ / / / / \ \ \ \ / /
\ \/ / / / \ \ \ \/ /
\ / / / \ \ \ /
\ \ / / \ \ / /
\ \_/ / \ \_/ /
\ / \ /
| | | |
| | | |
| | = | |
| | | |
| | | |
| | | |
| | | |
| | | |
The idea here is that if you draw the picture on the left-hand side on
a sheet of rubber, you can warp the rubber until it looks like the
right-hand side! There's also the "coassociative law", which is
just an upside-down version of the above picture. But the most
interesting laws are the "I = N" equation:
\ \ / / | | | |
\ \ / / | | | |
\ \_/ / | | | |
\ / | \ | |
| | | \ | |
| | | |\ \ | |
| | | | \ \ | |
| | | | \ \ | |
| | = | | \ \ | |
| | | | \ \ | |
| | | | \ \| |
| | | | \ |
/ _ \ | | \ |
/ / \ \ | | | |
/ / \ \ | | | |
/ / \ \ | | | |
and its mirror-image version.
So, the concept of Frobenius algebra captures the topology of regions in the plane! Aaron Lauda makes this fact into a precise theorem in his paper on planar open string field theories, and then generalizes it to consider "categorified" Frobenius algebras where the above equations are replaced by isomorphisms, which describe the process of warping the sheet of rubber until the left side looks like the right. You should look at his paper even if you don't understand the math, because it's full of cool pictures.
Lauda and Pfeiffer's paper goes still further, by considering these paint stripes as "open strings", not living in the plane anymore, but zipping around in some spacetime of high dimension, where they might as well be abstract 2-manifolds with corners. Following Moore and Segal, they also bring "closed strings" into the game, which form a Frobenius algebra of their own, where the multiplication looks like an upside-down pair of pants:
O O
\ \ / /
\ \ / /
\ /
| |
| |
| |
| |
| |
O
These topological closed strings are the subject of Joachim Kock's
book mentioned in "week202";
they correspond to commutative Frobenius algebras. The fun new
stuff comes from letting the open strings and closed strings interact.
You can read more about Lauda and Pfeiffer's work at Urs Schreiber's blog:
17) Urs Schreiber, Lauda and Pfeiffer on open-closed topological strings, http://golem.ph.utexas.edu/string/archives/000680.html
In fact, I recommend Schreiber's blog quite generally to anyone interested in higher categories and/or the math of string theory!
Addendum: Bruce Smith, David Rusin and Robert Lupton had some comments about the astronomy section; Urs Schreiber had more to say about the role of Frobenius algebras in string theory.
Bruce Smith picked up on my comment about accretion disks being common at many different scales, and wondered what the smallest accretion disks are. We talked about it and agreed that hurricanes, tornados, dust devils and whirlpools are related phenomena, but not true accretion disks.
Given this, the smallest accretion disks I know are those that led to the formation of planets in our Solar System, and perhaps even some moons. These probably began as eddies in the bigger accretion disk that became our Sun. The Sun is about 300,00 times heavier than the Earth, and the super-massive black hole in M87 is about 3 billion times heavier than the Sun, so we're seeing accretion disks that differ in mass by a factor of a trillion!
David Rusin's reaction to Hoag's object was:
Cool. But what are the chances that there would be not just one but TWO fascinating objects which have a significant plane of symmetry, which "just happens" to be perpendicular to our line of sight?He asked how many ring galaxies are known!
I checked and read there are 100 known "polar-ring galaxies". Here's a nice one called NGC 4650:
18) Ring around a galaxy, HubbleSite News Archive, May 6, 1999, http://hubblesite.org/newscenter/newsdesk/archive/releases/1999/16/image/a
I can imagine this thing looking like Hoag's object if we viewed it head-on.
Here's another ring galaxy, called AM 0644-741:
19) The lure of the rings, Hubblesite News Archive, April 22, 2004, http://hubblesite.org/newscenter/newsdesk/archive/releases/2004/15/image/a
It's the result of a collision involving a galaxy that's not in this picture. So, maybe Hoag's object is just a specially pretty case of a galaxy collision!
Robert Lupton referred me to a picture that covers more of the Virgo Cluster - but the file is huge, so I won't include it here:
20) Doug Finkbeiner and the Sloan Digital Sky Survey Consortium, Some pretty objects as observed by the SDSS: Virgo Cluster, http://www.astro.princeton.edu/~rhl/dfink
See the lower right corner for the picture called "virgobig".
Here's what Urs Schreiber had to say about Frobenius algebras and string theory:
John Baez wrote:Here's the paper Urs refers to:[...] Following Moore and Segal, they also bring "closed strings" into the game, which form a Frobenius algebra of their own, where the multiplication looks like an upside-down pair of pants: [...]I would like to make the following general comment on the meaning of Frobenius algebras in 2-dimensional quantum field theory.
Interestingly, non-commutative Frobenius algebras play a role even for closed strings, and even if the worldhseet theory is not purely topological.
The archetypical example for this is the class of 2D TFTs invented by Fukuma, Hosono and Kawai. There one has a non-commutative Frobenius algebra which describes not the splitting/joining of the entire worldsheet, but rather the splitting/joining of edges in any one of its dual triangulations. It is the center of (the Morita class of) the noncommutative Frobenius algebra decorating dual triangulations which is the commutative Frobenius algebra describing the closed 2D TFT.
One might wonder if it has any value to remember a non-commutative Frobenius algebra when only its center matters (in the closed case). The point is that the details of the non-commutative Frobenius algebra acting in the "interior" of the world sheet affects the nature of "bulk field insertions" that one can consider and hence affects the (available notions of) n-point correlators of the theory, for n > 0.
This aspect, however, is pronounced only when one switches from 2D topological field theories to conformal ones.
The fascinating thing is that even 2D conformal field theories are governed by Frobenius algebras. The difference lies in different categorical internalization. The Frobenius algebras relevant for CFT don't live in Vect, but in some other (modular) tensor category, usually that of representations of some chiral vertex operator algebra. It is that ambient tensor category which "knows" if the Frobenius algebra describes a topological or a conformal field theory (in 2D) - and which one.
Of course what I am referring to here is the work by Fjelstad, Froehlich, Fuchs, Runkel, Schweigert and others. I can recommend their most recent review which will appear in the Streetfest proceedings. It is available as math.CT/0512076.
The main result is, roughly, that given any modular tensor category with certain properties, and given any (symmetric and special) Frobenius algebra object internal to that category, one can construct functions on surfaces that satisfy all the properties that one would demand of an n-point function of a 2D (conformal) field theory.
If we define a field theory to be something not given by an ill-defined path integral, but something given by its set of correlation functions, then this amounts to constructing a (conformal) field theory.
This result is achieved by first defining a somewhat involved procedure for generating certain classes of functions on marked surfaces, and then proving that the functions generated by this procedure do indeed satisfy all the required properties.
In broad terms, the prescription is to choose a dual triangulation of the marked worldsheet whose correlation function is to be computed, to decorate its edges with symmetric special Frobenius algebra objects in some modular tensor category, to decorate its vertices by product and coproduct morphisms of this algebra, to embed the whole thing in a certain 3-manifold in a certain way and for every boundary or bulk field insertion to add one or two threads labeled by simple objects of the tensor category which connect edges of the chosen triangulation with the boundary of that 3-manifold. Then you are to hit the resulting extended 3-manifold with the functor of a 3D TFT and hence obtain a vector in a certain vector space. This vector, finally, is claimed to encode the correlation function.
This procedure is deeply rooted in well-known relations between 3-(!)-dimensional topological field theory, modular functors and modular tensor categories and may seem very natural to people who have thought long enough about it. It is already indicated in Witten's paper on the Jone's polynomial, that 3D TFT (Chern-Simons field theory in that case) computes conformal blocks of conformal field theories on the boundaries of these 3-manifolds. To others, like me in the beginning, it may seem like a miracle that an involved and superficially ad hoc procedure like this has anything to do with correlations functions of conformal field theory in the end.
In trying to understand the deeper "meaning" of it all I played around with the idea that this prescription is really, to some extent at least, the "dual" incarnation of the application of a certain 2-functor to the worldsheet. Namely a good part of the rough structure appearing here automatically drops out when a 2-functor applied to some 2-category of surfaces is "locally trivialized". I claim that any local trivialization of a 2-functor on some sort of 2-category of surface elements gives rise to a dual triangulation of the surface whose edges are labeled by (possibly a generalization of) a Frobenius algebra object and whose vertices are labeled by (possibly a generalization of) product and coproduct operations. There is more data in a locally trivialized 2-functor, and it seems to correctly reproduce the main structure of bulk field insertions as appearing above. But of course there is a limit to what a 2-functor can know about a structure that is inherently 3-dimensional.
I have begun outlining some of the details that I have in mind here:
http://golem.ph.utexas.edu/string/archives/000697.html
This has grown out of a description of gerbes with connective structure in terms of transport 2-functors. Note that in what is called a bundle gerbe we also do have a certain product operation playing a decisive role. Bundle gerbes can be understood as "pre-trivializations" of 2-functors to Vect:
http://golem.ph.utexas.edu/string/archives/000686.html
and the product appearing is one of the Frobenius products mentioned above. For a bundle gerbe the coproduct is simply the inverse of the product, since this happens to be an isomorphism. The claim is that 2-functors to Vect more generally give rise to non-trivial Frobenius algebras when locally trivialized.
This is work in progress and will need to be refined. I thought I'd mention it here as a comment to John's general statements about how Frobenius algebras know about 2-dimensional physics. I am grateful for all kinds of comments.
21) Ingo Runkel, Jens Fjelstad, Jurgen Fuchs and Christoph Schweigert, Topological and conformal field theory as Frobenius algebras, available as math.CT/0512076.
© 2005 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|