




|
 
|

|
I'm visiting Chicago now. I came just in time for a conference in honor of Saunders Mac Lane, one of the founders of category theory, who taught at the University of Chicago for many years and died last year at the age of 95:
1) Category Theory and its Applications: A Conference in Memory of Saunders Mac Lane, http://www.math.uchicago.edu/~may/MACLANE/
On Friday there was a memorial service where the friends and family of Mac Lane spoke about him, and a kind of reminiscence session where everyone could tell their favorite stories involving him. Then there were a bunch of math talks, both by people with strong connections to Mac Lane - Peter Johnstone, Bill Lawvere, Peter Freyd, Ieke Moerdijk, Peter May and Steve Awodey - and by people working on higher categories and their applications.
My own connection to Mac Lane is tiny. Everything I do uses his work, but that's true of lots of mathematicians: he discovered so much. Apart from watching him celebrate his 90th birthday at a category theory conference in Portugal back in 1999, the best moment happened when I came to Chicago and gave a talk. He invited me up to his office and we talked a bit. He told me I should write a book explaining n-categories. I promised I would... I was too shy to say much.
Now I'm trying to write that book, and I just happen to be staying in Mac Lane's old office, which makes me feel especially obliged to do it. This office is on the third floor of the Ryerson Physical Laboratory. It has a very high ceiling, and one wall is lined with two stacks of metal bookshelves. You'd need a ladder to reach the top! When I spoke to Mac Lane in his office, they were all full of books. Alas, they're empty now.
Next time I'll say a bit about Julie Bergner's talk at the Maclane memorial conference - she spoke about derived categories of quiver representations and quantum groups. But the conference was so intense and exhausting that first I need to recover by thinking about something completely different. So, I'll concentrate on last week's puzzle about rational tangles.
But first: the astronomy picture of the week!
It'll be more fun after a little background. The northern part of Mars is very different from the rest. It's much smoother, and the altitude is much less:
2) Linda M. V. Martel, Ancient floodwaters and seas on Mars, http://www.psrd.hawaii.edu/July03/MartianSea.html
Why is this?
Many scientists believe the north was an ocean during the Hesperian Epoch, a period of Martian history that stretches from about 3.5 to about 1.8 billion years ago. In particular, the beautifully named "Vastitas Borealis", an enormous plain that covers most of northern Mars, has textures that may have been formed by an ocean that froze and then slowly sublimated. (Sublimation is what happens when ice turns directly into water vapor without actually melting.) Mike Carr and James Head wrote a paper suggesting that around the end of the Hesperian, about 30% of the water on Mars evaporated and left the atmosphere, drifting off into outer space... part of the danger of life on a planet without much gravity:
3) M. H. Carr and J. W. Head, III, Oceans of Mars: An assessment of the observational evidence and possible fate, Journal of Geophysical Research 108 (2003), 5042.
The rest of the water is now frozen at the poles or lurking underground.
And that brings us to our picture. Here's some ice in a crater in Vastitas Borealis:
4) Water ice in crater at Martian north pole, European Space Agency (ESA), http://www.esa.int/esaMI/Mars_Express/SEMGKA808BE_3.html
Perhaps this is a remnant of a once mighty ocean!
The picture is close to natural color, but the vertical relief is exaggerated by a factor of 3. The crater is 35 kilometers wide and 2 kilometers deep. It's incredible how they can get this kind of picture from satellite photos and lots of clever image processing. I hope they didn't do too much stuff just to make it look pretty.
Next: rational tangles.
In "week228", I asked for help understanding the connection between rational tangles and the group PSL(2,Z). I got a great reply from Michael Hutchings, which winds up relating these ideas to the branched double cover of the sphere by the torus. And, this gives me an excuse to tell you some stuff I learned from James Dolan about elliptic functions and a map of the world called "Peirce's quincuncial".
So, let's dive in!
Did you ever try to wrap a sphere around itself twice? Mentally, I mean? Slit it open, grab it, pull it, stretch it, wrap it around itself twice, and glue the seams back together?
It's not hard. You just take the Riemann sphere - the complex numbers together with a point at infinity - and map it to itself by the function
f(z) = z2
If you think of the sphere as the surface of the Earth, with zero at the south pole and infinity as the north pole, this function doubles the longitude. So, it wraps the sphere around itself twice!
I hope you're visualizing this.
This function is not quite a "double cover", because it's not quite two-to-one everywhere. Only one point gets mapped to z = 0, namely itself, and only one point gets mapped to z = ∞, namely itself. Elsewhere f is two-to-one.
If you walk once around the north pole or south pole, and then apply the function f to your path, you get a path that goes around these points twice. Summarizing these properties, we call the function a "branched double cover" of the sphere by itself, with zero and infinity as branch points.
Now, how about wrapping a torus twice around a sphere?
This too can be done. It turns out there's a nice branched double cover of the sphere by the torus, which has four branch points.
To visualize this, first take the surface of the Earth and mold it into a regular octahedron. There will be six corners: the north pole, the south pole, the east pole, the west pole, the front pole and the back pole. Now take the octahedron and unfold it like this:
S-----B-----S | /|\ | | / | \ | | / | \ | | / | \ | |/ | \| W-----N-----E |\ | /| | \ | / | | \ | / | | \ | / | | \|/ | S-----F-----S
o o o o o
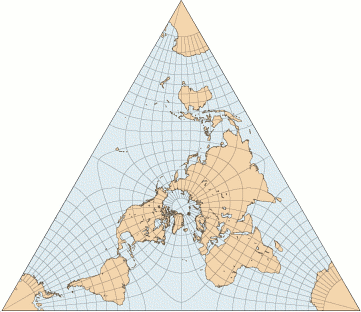
This is how Peirce's quincuncial looks as an actual map:
5) Carlos A. Furuti, Conformal projections, http://www.progonos.com/furuti/MapProj/Normal/ProjConf/projConf.html
The cool part is that you can tile the plane indefinitely with this map:
S-----B-----S-----F-----S-----B-----S-----F-----S | /|\ | /|\ | /|\ | /|\ | | / | \ | / | \ | / | \ | / | \ | | / | \ | / | \ | / | \ | / | \ | | / | \ | / | \ | / | \ | / | \ | |/ | \|/ | \|/ | \|/ | \| W-----N-----E-----N-----W-----N-----E-----N-----W |\ | /|\ | /|\ | /|\ | /| | \ | / | \ | / | \ | / | \ | / | | \ | / | \ | / | \ | / | \ | / | | \ | / | \ | / | \ | / | \ | / | | \|/ | \|/ | \|/ | \|/ | S-----F-----S-----B-----S-----F-----S-----B-----S | /|\ | /|\ | /|\ | /|\ | | / | \ | / | \ | / | \ | / | \ | | / | \ | / | \ | / | \ | / | \ | | / | \ | / | \ | / | \ | / | \ | |/ | \|/ | \|/ | \|/ | \| E-----N-----W-----N-----E-----N-----W-----N-----E
This gives a branched cover of the sphere by the plane! It has branch points at the east, west, front and back poles, since walking once around a point like that on the above map corresponds to walking around it twice on the actual Earth. This is pretty weird, but Peirce cleverly located two of these branch points in the Pacific Ocean, one in the Atlantic, and one in the Indian Ocean.
We can be less extravagant and get a branched cover of the sphere by the torus if we take the smallest parallelogram whose opposite edges match up:
B
/|\
/ | \
/ | \
/ | \
/ | \
E-----N-----W
/|\ | /|\
/ | \ | / | \
/ | \ | / | \
/ | \ | / | \
/ | \|/ | \
B-----S-----F-----S-----B
\ | /|\ | /
\ | / | \ | /
\ | / | \ | /
\ | / | \ | /
\|/ | \|/
W-----N-----E
\ | /
\ | /
\ | /
\ | /
\|/
B
This function is mostly two-to-one, but it's one-to-one at the points labelled E, F, W, and B. After all, there's just one point of each of these sorts in the above picture after we glue together the opposite edges. There are two copies of any other sort of point.
So, our function is a branched double cover of the sphere by the torus, which has four branch points. In fact, this function is quite famous. It's an example of an "elliptic function"!
I explained elliptic functions way back in "week13". Briefly, what we just did starting with this parallelogram:
B
/|\
/ | \
/ | \
/ | \
/ | \
E-----N-----W
/|\ | /|\
/ | \ | / | \
/ | \ | / | \
/ | \ | / | \
/ | \|/ | \
B-----S-----F-----S-----B
\ | /|\ | /
\ | / | \ | /
\ | / | \ | /
\ | / | \ | /
\|/ | \|/
W-----N-----E
\ | /
\ | /
\ | /
\ | /
\|/
B
As before, this is a branched double cover with four branch points. However, where the branch points sit on the sphere depends on the shape of the parallelogram. By picking the parallelogram carefully, you can put the branch points wherever you want! Peirce's neat idea was to put them evenly spaced along the equator - at the east, front, west and back poles. This is nice and symmetrical.
It's also especially nice to put the branch points at the vertices of a regular tetrahedron. I'm not sure, but this may give a map developed by the cartographer Laurence P. Lee in 1965. There's also a picture of this on Furuti's webpage:
In fact, these two specially nice locations for branch points correspond to the two most symmetrical lattices in the plane: the square one and the hexagonal one. I talked about these in "week125" - they're really important in the theory of elliptic functions, and even in string theory.
Anyway: for any parallelogram we can make a map of the Earth that tiles the plane, with tiles shaped like this parallelogram. A cool thing about these maps is that they're all "conformal" - they preserve angles except at the branch points. If you want to show off, you express this by saying "elliptic functions are complex analytic".
But now I'm digressing a little. Let's get back on track. What does all this have to do with rational tangles??
Recall my puzzle from last time. We build rational tangles by starting with the trivial one, which we call "zero"
| | | | | | | |and repeatedly doing two operations. The first is a twisting operation that we call "adding one":
| | | | | | | | | | | | ------- ------- | T | |----> | T | = "T + 1" ------- ------- | | \ / | | / | | / \where the box labelled "T" stands for any tangle we've built so far. The second is a rotation that we call "negative reciprocal":
| | | | | | | | ____ | | | | / \ ------- | ------- | | T | |----> | | T | | = "-1/T" ------- | ------- | | | \___/ | | | | | | | | | |Using these tricks we can try to assign a rational number to any rational tangle. The shocking theorem is that this number is indeed well-defined, and in fact a complete invariant of rational tangles.
Every operation built from "adding one" and "negative reciprocal" looks like this:
az + b
z |-> -------
cz + d
with a,b,c,d integer and ad-bc = 1. The group of these transformations
is called PSL(2,Z). This group acts on the rational numbers together
with a point at infinity (the "rational projective line") by the formula
above. It also acts on rational tangles. The puzzle is to see why these
actions are isomorphic. The proofs I listed in "week228" show it's true;
the problem is to understand what's really going on!
Here's the answer given by Michael Hutching on sci.math.research:
There's a simple topological interpretation of the element of the rational projective line associated to a rational tangle. I don't know how to use this to prove the theorem, and I don't know a reference for it (maybe it is in one of the references you cited). Anyway, regard a rational tangle as a two-component curve C in the 3-ball B3 whose four boundary points are on the 2-sphere S2. Consider the double branched cover of B3 along C. This is a 3-manifold Y whose boundary can be identified with the 2-torus T2. (In fact Y is a solid torus.) The inclusion of T2 into Y induces a map from H1(T2) to H1(Y), and the kernel of this map is a one-dimensional subspace of H1(T2) = Z2. If I am not mistaken, this is the element in question of the rational projective line.In other words, we take a 3-dimensional ball and draw a picture of a rational tangle in it:
.......
. | | .
. ----- .
. | T | .
. ----- .
. | | .
.......
This gets the torus into the game, and also the branched cover I was talking about. And this gets the group PSL(2,Z) into the game! SL(2,Z) is the group of 2×2 matrices with determinant 1. When you mod out by the matrices +-1, you get PSL(2,Z). But, topologists know that SL(2,Z) is the "mapping class group" of the torus - the group of orientation-preserving diffeomorphisms modulo those that can be smoothly deformed to the identity.
So, something nice is happening.
Even better, the rational first homology group of the torus is Q2 (pairs of rational numbers), and SL(2,Z) acts in the obvious way, by matrix multiplication:
a b x ax + by
: |->
c d y cx + dy
It therefore acts on the set of 1-dimensional subspaces of Q2.
Any such subspace consists of vectors like this:
kx kyThe subspace is determined by the ratio x/y, which however could be infinite - so it's just a point in the rational projective line. So, we get an action of SL(2,Z) on the rational projective line. Indeed we get an action of PSL(2,Z) since +-1 act trivially. And, you can easily check that it's the action we've already seen:
a b az + b
: z |-> --------
c d cz + d
In short: "projectivizing" the action of mapping class group of the
torus on its first homology gives the usual action of PSL(2,Z) on the
rational projective line.
What we need next is a natural way to assign to any rational tangle a 1-dimensional subspace of the homology of the torus. And this is what Hutchings describes: a rational tangle gives a way of mapping the torus T2 into the solid torus Y, and this gives a map on rational homology
H1(T2) → H1(Y)
whose kernel is a 1-dimensional subspace of H1(T2).
There's more stuff to check....
Personally I've been trying to think of the mapping class group of the 4-punctured sphere as acting on pictures like this:
.......
. | | .
. ----- .
. | T | .
. ----- .
. | | .
.......
| | | | | | | | | | | | ------- ------- | T | |----> | T | ------- ------- | | \ / | | / | | / \and the 90 degree rotation
| | | | | | | | ____ | | | | / \ ------- | ------- | | T | |----> | | T | | ------- | ------- | | | \___/ | | | | | | | | | |and our homomorphism should map these to the famous matrices
1 1
T = "shear"
0 1
and
0 -1
S = "90 degree rotation"
1 0
respectively. If this works, and I could figure out the kernel of
this homomorphism and show it acts trivially on rational tangles,
I think I'd be almost done. But, I haven't had time!
By the way, if this works, there's a beautiful little sideshow where we use as generators of SL(2,Z) not the above matrices but S and
0 -1
ST =
1 1
I explained why these are so great in "week125". S is a symmetry of
the square lattice, while ST is a symmetry of the hexagonal lattice.
The square lattice gives Peirce's quincuncial map, while the hexagonal
one presumably gives Laurence Lee's triangular map!
So, there's some intriguing story about elliptic functions and rational tangles taking shape before our eyes.... and if I weren't so darn busy, I'd figure out all the details and write a little paper about it.
Before quitting, there's one more thing I can't resist mentioning. Any ordered 4-tuple of points (a,b,c,d) in the Riemann sphere gives a number called its "cross-ratio":
(a-b)(c-d) / (a-d)(c-b)
It's a famous fact that you can find a conformal transformation of the Riemann sphere mapping one ordered 4-tuple to another if and only if their cross-ratios are equal!
So, we can play a little trick. Given a lattice we can get a branched double cover of the Riemann sphere as I sketched earlier. Then we can use the location of the branch points to calculate a cross ratio.
But actually, I'm being a bit sloppy here. To compute a cross ratio from a lattice, we need some extra information to order the 4-tuple of branch points. In other words, if one of the points S is the origin here:
S-----B-----S-----F-----S-----B-----S-----F-----S | /|\ | /|\ | /|\ | /|\ | | / | \ | / | \ | / | \ | / | \ | | / | \ | / | \ | / | \ | / | \ | | / | \ | / | \ | / | \ | / | \ | |/ | \|/ | \|/ | \|/ | \| W-----N-----E-----N-----W-----N-----E-----N-----W |\ | /|\ | /|\ | /|\ | /| | \ | / | \ | / | \ | / | \ | / | | \ | / | \ | / | \ | / | \ | / | | \ | / | \ | / | \ | / | \ | / | | \|/ | \|/ | \|/ | \|/ | S-----F-----S-----B-----S-----F-----S-----B-----S | /|\ | /|\ | /|\ | /|\ | | / | \ | / | \ | / | \ | / | \ | | / | \ | / | \ | / | \ | / | \ | | / | \ | / | \ | / | \ | / | \ | |/ | \|/ | \|/ | \|/ | \| E-----N-----W-----N-----E-----N-----W-----N-----E
Hmm, this is getting pretty jargonesque! I don't want to explain the jargon now, but you can read all about this trick and its consquences in Lecture 9 here:
6) Igor V. Dolgachev, Lectures on modular forms, Fall 1997/8, available at http://www.math.lsa.umich.edu/~idolga/modular.pdf
Addenda: Andrei Sobolevskii points out that the etymology of the word "quincunx" is explained here:
7) Quincunx, World Wide Words, http://www.worldwidewords.org/weirdwords/ww-qui2.htm
Very briefly, "quincunx" was a Latin word for "five twelfths", from quinque and uncia. The latter word is also the root of the word "ounce". They had a copper coin called the as weighing twelve ounces (!), and the quincunx was apparently not a coin a symbol for 5/12 of an as - or in other words, 5 ounces of copper.
After reading the above, Peter Dickof clarified and corrected the story:
Love "This Week's Finds" (though I seldom follow it all) and can't pass up the opportunity to say something.My old pal Squark noted some sloppy language about branched covers. Here's my reply to what he wrote. I've changed what he wrote a tiny bit, for cosmetic reasons.The as was indeed a unit of currency and also a specific bronze coin. Early asses (aes = bronzes - hence the AE ligature...) were full Roman pounds (librae -hence the British pound "£" sign) of 288 scruples with twelve unciae to the pound. Each uncia was ~27 grams, a modern ounce near enough. Debasement set in around the time of the first Punic war and accelerated through the second (Hannibal's), by the end of which an as, still of bronze, weighed only ~30 grams.
Multiples of the as were minted (misnomer, this was a cast currency): the decussis (X asses), quincussis (V asses), tressis (III asses), and the dupondius (two-pounder). The asses were marked with the Roman numeral I. Common fractions were the semis (half, marked with an S), triens (third, sometimes called a quatrunx, marked with four "pellets" or dots), quadrans (quarter, also teruncius, 3 pellets), sextans (sixth, also biunx, 2 pellets), uncia and semuncia (usually unmarked).
There were quincunx coins (5 pellets), and also a dextans (S + 4 pellets), mostly produced by non-Roman Italians. I have appended photos of three quincunxes produced in Luceria (see Thurlow and Vecchi numbers 274, 281). Note that the "pellets" are sometimes (not always) arranged in a quincunx. Luceria (modern Lucera) is 2/3 of the way across the boot from Neapolis (Naples).
During the second Punic war, after they captured Syracuse and its treasure (and killed Archimedes), the Romans introduced the silver denarius, quinarius and sesterius; they were worth 10, 5, 2 1/2 (IIS) asses. The denarius is the origin of the "d" for the British shilling, and was about the size of a dime. Later, circa 141 BC, the value of silver was re-tariffed so that denarii, quinarii and sestertii became worth 16, 8, 4 asses; the names did not change but the quinarius and sestertius became rare.
Julius Caesar doubled the pay of a legionary to 300 sestertii per installment (stipendium), 3 installments per year.
Later yet, during Imperial Rome, the largest bronze/brass coin minted (no longer a misnomer) was a sestertius; its weight was less than 30 grams by the time of Claudius and falling, always falling....
Appropriate references are:
- Michael H. Crawford, Roman Republican Coinage, Cambridge University Press, Cambridge, 1974. (See picture of Quincunx on plate XVIII.)
- Bradbury K. Thurlow, Italian Cast Coinage, Italian Aes Grave. Italo G. Vecchi, Italian Aes Rude, Signatum and the Aes Grave of Sicily. Printed together by Veechi, London, 1979.
- Herbert A. Grueber, A Catalogue of the Coins of the Roman Republic in the British Museum, three volumes, reprinted 1970.
Squark wrote:>Hello John and everyone!Hello! Long time no see! How are you doing?I had written:
>There's a simple topological interpretation of the element of the >rational projective line associated to a rational tangle. I don't know >how to use this to prove the theorem, and I don't know a reference for >it (maybe it is in one of the references you cited). Anyway, >regard a rational tangle as a two-component curve C in the 3-ball >B3 whose four boundary points are on the 2-sphere S2. >Consider the double branched cover of B3 along C.Squark wrote:>What is "_the_ double branched cover"? Is there a way to choose a >canonical one, or is there only one in this case, for some reason?Good point. I hope there's a specially nice one.To pick a branched cover of B3 along C, it's necessary and sufficient to pick a homomorphism from the fundamental group of B3 - C to Z/2. This says whether or not the two sheets switch places as we walk around C following some loop in B3 - C.
>In the case of a sphere with 4 points removed it should be easy to >check.Yes.>The fundamental group has 4 generators - a, b, c, d (loops around >each of the points) and one relation abc = d (since we're on a >sphere). Hence, it is freely generated by a, b, c (say).Right, the fundamental group of the four-punctured sphere is the free group on 3 generators, F3. I believe the "specially nice" homomorphismf: F3 → Z/2
is the one that sends each generator to -1, where I'm thinking multiplicatively:
Z/2 = {1, -1}
One reason this homomorphism is especially nice is that it also sends d = abc to -1.
So, if you walk around ANY of the four punctures, the two sheets switch!
This is just what you want for the Riemann surface of an elliptic integral, as someone else pointed out in another post: there are four branch points each like the branch point of √z. It's also the most symmetrical, beautiful thing one can imagine.
Now let's see if and how this branched cover extends to a branched cover of the ball B3 with C (two arcs) removed. The fundamental group of B3 - C is the free group on two generators, say X and Y.
The inclusion of the 4-punctured sphere in B3 - C gives a homomorphism
g: F3 → F2
as follows:
a |→ X
b |→ X-1
c |→ Y
d |→ Y-1
So, to extend our branched cover, we need to write our homomorphism
f: F3 → Z/2
as
f = hg
for some homomorphism
h: F2 → Z/2
The obvious nice thing to try for h is
X |→ -1
Y |→ -1It works, and it's unique!
Lee Rudolph adds:
Squark wrote:>What is "_the_ double branched cover"? Is there a way to choose a >canonical one, or is there only one in this case, for some reason?John Baez wrote:>Good point. I hope there's a specially nice one.In this kind of context, there's always exactly one "double branched cover" that actually does branch doubly over every component of the proposed branch locus. In particular, in the context of a rational tangle, of course the pair (B3,C) is homeomorphic to (B2,X)×I, where X is a 2-point set in Int B2 and the homeomorphism isn't required to preserve the tangle structure; so the double branched cover of B3 branched over C is the product of the double branched cover of B2 branched over X with the interval I. Now, because the branching is double at each point of X, and there are two points of X, it follows that the monodromy around the boundary of B2 must be trivial, so that we can sew another B2 to that boundary and extend the branched double covering over the resulting 2-sphere. But of course the branched double cover of a 2-sphere over 2 points is another 2-sphere, the model for the situation being z |→ z2 as a map of the Riemann sphere to itself. Now remove the interior of the sewed-on second B2 from the downstairs S2, and correspondingly the interiors of its two preimage B2s from the upstairs S2; you see that the double cover of B2 branched over X is an annulus. (Once you know that, you can see it directly: take an annulus embedded in R3 as the cylinder where x2+y2=1 and -1 ≤ z ≤ 1; rotate it by 180 degrees around the x-axis, and convince yourself that the quotient space is a 2-disk by considering the fundamental domain consisting of those points of the annulus with non-negative y-coordinate.) Then the double cover of B3 branched over C must be a solid torus. (Again, now that you know this, you can see it directly: take the solid torus to be a tubular neighborhood in R3 of the circle where x2+y2=1 and z = 0, and again rotate by 180 degrees around the x-axis to give yourself the "deck involution".)Lee Rudolph
© 2006 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|