




|
 
|

|
I'm at the Perimeter Institute now. It's great to see how it's developed since I first saw their new building back in 2004 (see "week208" for the story).
There's now a busy schedule of seminars and weekly colloquia, with string theorists and loop quantum gravity people coexisting happily. Their program of Superstring Quartets features some really hot bands, like the Julliard and Emerson - unfortunately not playing while I'm here. The Black Hole Bistro serves elegant lunches and dinners, there are at least two espresso machines on each floor, and my friend Eugenia Cheng will be happy to hear that they still have a piano available (after 6 pm).
But don't get the impression that it's overly sophisticated: there are also a couple of guys constantly playing foosball in the Feynman Lounge.
Since I'm here, I should talk about quantum gravity - so I will. But first, let's have the astronomy picture of the week.
This week it comes, not from outer space, but beneath the surface of the South Pole:
1) Steve Yunck / NSF, Cerenkov light passing through the IceCube neutrino detector, http://icecube.wisc.edu/gallery/detector_concepts/ceren_hires
This is an artist's impression of a huge neutrino observatory called "IceCube". (Maybe they left out the space here so the rap star of that name doesn't sue them for trademark infringement, or go down there and shoot them.)
IceCube is being built in the beautifully clear 18,000-year old ice deep beneath the Amundsen-Scott South Pole Station. When a high-energy neutrino hits a water molecule, sometimes the collision produces a muon zipping faster than the speed of light in ice. This in turn produces something like a sonic boom, but with light instead of sound. It's called "Cerenkov radiation", and it's the blue light in the picture. This will be detected by an array of 5000 photomultiplier tubes - those gadgets hanging on electrical cables.
One thing the artist's impression doesn't show is that IceCube is amazingly large. The whole array is a cubic kilometer in size! It will encompass the already existing AMANDA detector, itself 10,000 meters tall, shown as a yellow cylinder here with a neutrino zipping through:
2) Darwin Rianto / NSF, Comparison of AMANDA and IceCube, http://icecube.wisc.edu/gallery/detector_concepts/icecubeencomp_300
Even the very top of IceCube is 1.4 kilometers beneath the snowy Antarctic surface, to minimize the effect of stray cosmic rays. The station on top looks like this - not very cozy, I'd say:
3) Robert G. Stokstad / NSF, South Pole Station, http://icecube.wisc.edu/gallery/antarctica/PC140287_300
I heard about IceCube from Adrian Burd, one of the old-timers who used to post a lot on sci.physics, a former cosmologist turned oceanographer who recently visited Antarctica as part of an NSF-run field course. He ran into some people working on IceCube. It sounds like an interesting community down there! You can read about it in their newspaper, the Antarctic Sun. For example:
4) Ice Cube turns up the heat, The Antarctic Sun, January 29, 2006, http://antarcticsun.usap.gov/2005-2006/contentHandler.cfm?id=959
For more on IceCube and Amanda, these are fun to read:
5) Francis Halzen, Ice fishing for neutrinos, http://icecube.berkeley.edu/amanda/ice-fishing.html
6) Katie Yurkiewicz, Extreme neutrinos, Symmetry, volume 1 issue 1, November 2004, http://symmetrymagazine.org/cms/?pid=1000014
For some of AMANDA's results, including a map of the sky as seen in neutrinos, try this:
7) M. Ackermann et al, Search for extraterrestrial point sources of high energy neutrinos with AMANDA-II using data collected in 2000-2002, available as astro-ph/0412347.
For much more, try these:
8) AMANDA II Project, http://amanda.uci.edu/
9) Welcome to IceCube, http://icecube.wisc.edu/
And now, on to gravity.
You may have heard of the gravitational 3-body problem. Well, Richard Montgomery (famous from "week181") recently pointed out this movie of the 60-body problem:
10) Davide L. Ferrario, Periodic orbits for the 60-body problem, http://www.matapp.unimib.it/~ferrario/mov/index.html
60 equal masses do a complicated dance while always preserving icosahedral symmetry! First 12 groups of 5 swing past each other, then 20 groups of 3. If you want to know how he found these solutions, read this:
11) Davide L. Ferrario and S. Terracini, On the existence of collisionless equivariant minimizers for the classical n-body problem. Invent. Math. 155 (2004), 305-362.
It's quite math-intensive - though just what you'd expect if you know this sort of thing: they use the G-equivariant topology of loop spaces, where G is the symmetry group in question (here the icosahedral group), to prove the existence of action-minimizing loops with given symmetry properties.
Next, I'd like to say a little about point particles in 3d quantum gravity, and some recent work with Alissa Crans, Derek Wise and Alejandro Perez on string-like defects in 4d topological gravity:
12) John Baez, Derek Wise and Alissa Crans, Exotic statistics for strings in 4d BF theory, available as gr-qc/0603085.
13) John Baez and Alejandro Perez, Quantization of strings and branes coupled to BF theory, available as gr-qc/0605087.
(Jeffrey Morton is also involved in this project, a bit more on the n-category side of things, but that aspect is top secret for now.)
In "week222" I listed a bunch of cool papers on 3d quantum gravity, but I didn't really explain them. What we're trying to do now is generalize this work to higher dimensions. But first, let me start by explaining the wonders of 3d quantum gravity.
The main wonder is that we actually understand it! The classical version of general relativity is exactly solvable when spacetime has dimension 3, and so is the quantum version. Most of the wonders I want to discuss are already visible in the classical theory, where they are easier to understand, so I'll focus on the classical case.
A nice formulation of general relativity in 3 dimensions uses a "Lorentz connection" A and a "triad field" e. This is a gauge theory where the gauge group is SO(2,1), the Lorentz group for 3d spacetime. If we're feeling lowbrow we can think of both A and e as so(2,1)-valued 1-forms on the 3-manifold M that describes spacetime. The action for this theory is:
∫M tr(e ^ F)
where F is the curvature of A. If you work out the equations of motion one of them says that F = 0, so our connection A is flat. The other, dAe = 0, says A is basically just the Levi-Civita connection.
This is exactly what we want, because in the absence of matter, general relativity in 3 dimensions says spacetime is flat.
A fellow named Phillipp de Sousa Gerbert came up with an interesting way to couple point particles to this formulation of quantum gravity:
14) Phillipp de Sousa Gerbert, On spin and (quantum) gravity in 2+1 dimensions, Nuclear Physics B346 (1990), 440-472.
He actually did it for particles with spin, but I'll just do the spin-zero case.
The idea is to fix a 1-dimensional submanifold W in our 3-manifold M and think of it as the worldlines of some particles. Put so(2,1)-valued functions p and q on these worldlines - think of these as giving the particles' momentum and position as a function of time.
Huh? Well, normally we think of position and momentum as vectors. In special relativity, "position" means "position in spacetime", and "momentum" means "energy-momentum". We can think of both of these as vectors in Minkowksi spacetime. But in 3 dimensions, Minkowski spacetime is naturally identified with the Lorentz Lie algebra so(2,1). So, it makes sense to think of q and p as elements of so(2,1) which vary from point to point along the particle's worldline.
To couple our point particles to gravity, we then add a term to the action like this:
S = ∫M tr(e ^ F) - ∫W tr((e + dAq) ^ p)
Now if you vary the e field you get a field equation saying that
F = p δW
Here δW is like the Dirac delta function of the worldline W; it's a distributional 2-form defined by requiring that
∫W X = ∫M (X ^ δW)
for any smooth 1-form X on W. This sort of "distributional differential form" is also called a "current", and you can read about them in the classic tome by Choquet-Bruhat et al. But the main point is that the field equation
F = p δW
says our connection on spacetime is flat except along the worldlines of our particles, where the curvature is a kind of "δ function". This is nice, because that's what we expect in 3d gravity: if you have a particle, spacetime will be flat everywhere except right at the particle, where it will have a singularity like the tip of a cone.
A cone, you see, is intrinsically flat except at its tip: that's why you can curl paper into a cone without crinkling it!
So, our spacetime is flat except along the particles' worldlines, and there it's like a cone. The "deficit angle" of this cone - the angle of the slice you'd need to cut out to curl some paper into this cone - is specified by the particle's momentum p.
Since delta functions are a bit scary, it's actually better to work with an "integrated" form of the equation
F = -p δW
The integrated form says that if we parallel transport a little tangent vector around a little loop circling our particle's worldline, it gets rotated and/or Lorentz transformed by the element
exp(p)
in SO(2,1). This will be a rotation if the particle's momentum p is timelike, as it is for normal particles. Again, that's just as it should be: if you parallel transport a little arrow around a massive particle in 3d gravity, it gets rotated!
If p is timelike, our particle is a tachyon and exp(p) is a Lorentz boost. And so on... we get the usual classification of particles corresponding to various choices of p:
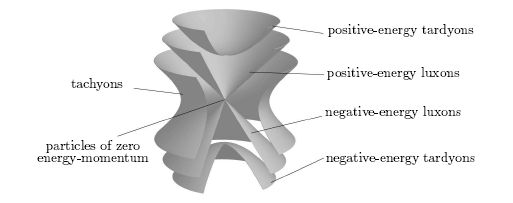
There are other equations of motion, obtained by varying other fields, but all I want to note is the one you get by varying q:
dA p = 0
This says that the momentum p is covariantly constant along the particles' worldlines. So, momentum is conserved!
The really cool part is the relation between the Lie algebra element p and the group element exp(p). Originally we thought of p as momentum - but there's a sense in which exp(p) is the momentum that really counts!
First, exp(p) is what we actually detect by parallel transporting a little arrow around our particle.
Second, suppose we let two particles collide and form a new one:
p p'
\ /
\ /
\ /
|
|
|
p"
Now our worldlines don't form a submanifold anymore, but if we keep
our wits about us, we can see that everything still makes sense, and
we get momentum conservation in this form:
exp(p") = exp(p) exp(p')
since little loops going around the two incoming particles can fuse to form a loop going around the outgoing particle. Note that we're getting conservation of the group-valued momentum, not the Lie-algebra-valued momentum - we don't have
p" = p + p'
So, conservation of energy-momentum is getting modified by gravitational effects! This goes by the name of "doubly special relativity":
15) Laurent Freidel, Jerzy Kowalski-Glikman and Lee Smolin, 2+1 gravity and doubly special relativity, Phys. Rev. D69 (2004) 044001. Also available as hep-th/0307085.
This effect is a bit less shocking if we put the units back in. I've secretly been setting 4πG = 1, where G is Newton's gravitational constant. If we put that constant back in - let's call it k instead of 4πG - we get
exp(kp") = exp(kp) exp(kp')
or if you expand things out:
p" = p + p' + (k/2) [p,p'] + terms of order k2 and higher...
So, as long as the momenta are small compared to the Planck mass, the usual law of conservation of momentum
p" = p + p'
almost holds! But, for large momenta this law breaks down - we must think of momentum as group-valued if we want it to be conserved!
I think this is incredibly cool: as we turn on gravity, the usual "flat" momentum space curls up into a group, and we need to multiply momenta in this group, instead of add them in the Lie algebra. We can think of this group has having a "radius" of 1/k, so it's really big and almost flat when the strength of gravity is small. In this limit, multiplication in the group reduces to addition in the Lie algebra.
I should point out that this effect is purely classical! It's still there when we quantize the theory, but it only depends on the gravitational constant, not Planck's constant. Indeed, in 3d quantum gravity, we can build a unit of mass using just G and c: we don't need ħ. This unit is the mass that curls space into an infinitely skinny cone! It would be a bit misleading to call it "Planck mass", but it's the maximum possible mass. Any mass bigger than this acts like a negative mass. That's because the corresponding group-valued momenta "wrap around" in the group SO(2,1).
We also get another cool effect - exotic statistics. In the absence of gravitational or quantum effects, when you switch two particles, you just switch their momenta:
(p, p') |→ (p', p)
But in 3d gravity, you can think of this process of switching particles as a braid:
\ /
\ /
\
/ \
/ \
and if you work out what happens to their group-valued momenta,
say
g = exp(kp)
g' = exp(kp')
it turns out that one momentum gets conjugated by the other:
(g, g') |→ (gg'g-1, g)
To see this, remember that we get these group elements by doing parallel transport around loops that circle our particles. When we move our particles, the loops get dragged along, like this:

(g, g') |→ (gg'g-1, g)
So, the process of braiding two particles around each other has a nontrivial effect on their momenta. In particular, if you braid two particles around other twice they don't wind up in their original state!
Thus, our particles are neither bosons nor fermions, but "nonabelian anyons" - the process of switching them is governed not by the permutation group, but by the braid group. But again, if you expand things out in powers of k you'll see this effect is only noticeable for large momenta:
(p, p') |→ (p' + k[p,p'] + higher order terms..., p)
Summarizing, we see quantum gravity is lots of fun in 3 dimensions: it's easy to introduce point particles, and they have group-valued momentum, which gives rise to doubly special relativity and braid group statistics.
Now, what happens when we go from 3 dimensions to 4 dimensions?
Well, we can write down the same sort of theory:
S = ∫M tr(B ^ F) - ∫W tr((B + dAq) ^ p)
The only visible difference is that what I'd been calling "e" is now called "B", so you can see why folks call this "BF theory".
But more importantly, now M is an 4-dimensional spacetime and W is an 2-dimensional "worldsheet". A is again a Lorentz connection, which we can think of as an so(3,1)-valued 1-form. B is an so(3,1)-valued 2-form. p is an so(3,1)-valued function on the worldsheet W. q is an so(3,1)-valued 1-form on W.
So, only a few numbers have changed... so everything works very similarly! The big difference is that instead of spacetime having a conical singularity along the worldline of a particle, now it's singular along the worldsheet of a string. When I call it a "string", I'm not trying to say it behaves like the ones they think about in string theory - at least superficially, it's a different sort of theory, a purely topological theory. But, we've got these closed loops that move around, split and join, and trace out surfaces in spacetime.
They can also braid around each other in topologically nontrivial ways, as shown in this "movie":
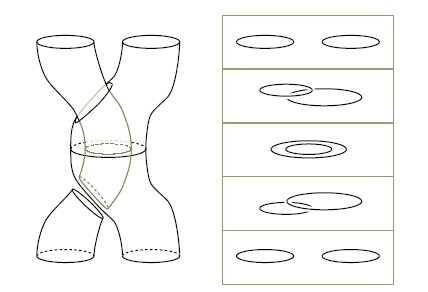
(By the way, all the math pictures this week were drawn by Derek for our paper.)
So, we get exotic statistics as before, but now they are governed not by the braid group but by the "loop braid group", which keeps track of all the ways we can move a bunch of circles around in 3d space. Let's take our spacetime M to be R4, to keep things simple. Then our circles can move around in R3... and there are two basic ways we can switch two of them: move them around each other, or pass one through the other, like this:
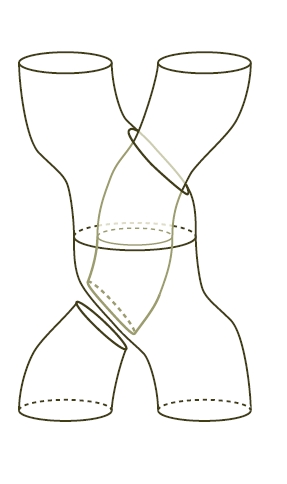
If we just move them around each other, they might as well have been point particles: we get a copy of the permutation group, and all we see are ordinary statistics. But when we consider all the ways of passing them through each other, we get a copy of the braid group!
When we allow ourselves both motions, we get a group called the "loop braid group" or "braid permutation group" - and one thing Alissa Derek and I did was to get a presentation of this group. This is an example of a "motion group": just as the motion group of point particles in the plane is the braid group, and motion group of point particles in R3 is the permutation group, the motion group of strings in R3 is the loop braid group.
As before, our strings have group-valued momenta: we can get an element of the Lorentz group SO(3,1) by parallel transporting a little tangent vector around a string. And, we can see how different ways of switching our strings affect the momenta. When we move two strings around each other, their momenta switch in the usual way:
(g, g') |→ (g', g)
but when we move one through the other, one momentum gets conjugated by the other:
(g, g') |→ (gg'g-1, g)
So, we have exotic statistics, but you can only notice them if you can pass one string through another!
In the paper with Alejandro, we go further and begin the project of quantizing these funny strings, using ideas from loop quantum gravity. Loop quantum gravity has its share of problems, but it works perfectly well for 3d quantum gravity, and matches the spin foam picture of this theory. People have sort of believed this for a long time, but Alejandro demonstrated this quite carefully in a recent paper with Karim Noui:
15) Karim Noui and Alejandro Perez, Dynamics of loop quantum gravity and spin foam models in three dimensions, to appear in the proceedings of the Third International Symposium on Quantum Theory and Symmetries (QTS3), available as gr-qc/0402112.
The reason everything works so nicely is that the equations of motion say the connection is flat. Since the same is true in BF theory in higher dimensions, we expect that the loop quantization and spin foam quantization of the theory I'm talking about now should also work well.
We find that we get a Hilbert space with a basis of "string spin networks", meaning spin networks that can have loose ends on the stringy defects.
So, there's some weird blend of loop quantum gravity and strings going on here - but I don't really understand the relation to ordinary string theory, if any. It's possible that I can get a topological string theory (some sort of well-defined mathematical gadget) which describes these stringy defects, and that would be quite interesting.
But, I spoke about this today at the Perimeter Institute, and Malcolm Perry said that instead of "strings" I should call these guys (n-2)-branes, because the connection has conical singularities on them, "which is what one would expect for any respectable (n-2)-brane".
I will talk to him more about this and try to pick his, umm, branes. In fact I took my very first GR course from him, back when he was a postdoc at Princeton and I was a measly undergraduate. I was too scared to ask him many questions then. I'm a bit less scared now, but I've still got a lot to learn. Tomorrow he's giving a talk about this:
17) David S. Berman, Malcolm J. Perry, M-theory and the string genus expansion, Phys. Lett. B635 (2006) 131-135. Also available as hep-th/0601141.
John Baez wrote:I replied:> The really cool part is the relation between the Lie algebra > element p and the group element exp(p). Originally we thought > of p as momentum - but there's a sense in which exp(p) is the > momentum that really counts!Would it be correct to assume that the ordinary tangent vector p still transforms in the usual way? In other words, suppose I'm living in a 2+1 dimensional universe, and there's a point particle with rest mass m and hence energy-momentum vector in its rest frame of p=me0. If I cross its world line with a certain relative velocity, there's an element g of SO(2,1) which tells me how to map the particle's tangent space to my own. Would I measure the particle's energy-momentum to be p'=gp? (e.g. if I used the particle to do work in my own rest frame) Would there still be no upper bound on the total energy, i.e. by making our relative velocity close enough to c, I could measure the particle's kinetic energy to be as high as I wished?I guess I'm trying to clarify whether the usual Lorentz transformation of the tangent space has somehow been completely invalidated for extreme boosts, or whether it's just a matter of there being a second definition of "momentum" (defined in terms of the Hamiltonian) which transforms differently and is the appropriate thing to consider in gravitational contexts.
In other words, does the cut-off mass apply only to the deficit angle, and do boosts still allow me to measure (by non-gravitational means) arbitrarily large energies (at least in the classical theory)?
Greg Egan wrote:>John Baez wrote: >>The really cool part is the relation between the Lie algebra >>element p and the group element exp(p). Originally we thought >>of p as momentum - but there's a sense in which exp(p) is the >>momentum that really counts! >Would it be correct to assume that the ordinary tangent vector p >still transforms in the usual way?Hi! Yes, it would.>In other words, suppose I'm living in a 2+1 dimensional universe, >and there's a point particle with rest mass m and hence >energy-momentum vector in its rest frame of p=m e_0. If I >cross its world line with a certain relative velocity, there's >an element g of SO(2,1) which tells me how to map the particle's >tangent space to my own. Would I measure the particle's >energy-momentum to be p'=gp? (e.g. if I used the particle to >do work in my own rest frame) Would there still be no upper >bound on the total energy, i.e. by making our relative velocity >close enough to c, I could measure the particle's kinetic energy >to be as high as I wished?To understand this, it's good to think of the momenta as elements of the Lie algebra so(2,1) - it's crucial to the game.Then, if you have momentum p, and I zip past you, so you appear transformed by some element g of the Lorentz group SO(2,1), I'll see your momentum as
p' = g p g-1
This is just another way of writing the usual formula for Lorentz transforms in 3d Minkowski space. No new physics so far, just a clever mathematical formalism.
But when we turn on gravity, letting Newton's constant k be nonzero, we should instead think of momentum as group-valued, via
h = exp(kp)
and similarly
h' = exp(kp')
Different choices of p now map to the same choice of h. In particular, a particle of a certain large mass - the Planck mass- will turn out to act just like a particle of zero mass!
So, if we agree to work with h instead of p, we are now doing new physics. This is even more obvious when we decide to multiply momenta instead of adding them, since multiplication in SO(2,1) is noncommutative!
But, if we transform our group-valued momentum in the correct way:
h' = ghg-1
this will be completely compatible with our previous transformation law for vector-valued momentum!
>I guess I'm trying to clarify whether the usual Lorentz transformation >of the tangent space has somehow been completely invalidated for >extreme boosts, or whether it's just a matter of there being a second >definition of "momentum" (defined in terms of the Hamiltonian) which >transforms differently and is the appropriate thing to consider in >gravitational contexts.Good question! Amazingly, the usual Lorentz transformations still work EXACTLY - even though the rule for adding momentum is new (now it's multiplication in the group). We're just taking exp(kp) instead of p as the "physical" aspect of momentum.This effectively puts an upper limit on mass, since as we keep increasing the mass of a particle, eventually it "loops around" SO(2,1) and act exactly like a particle of zero mass.
But, it doesn't exactly put an upper bound on energy-momentum, since SO(2,1) is noncompact. Of course energy and momentum don't take real values anymore, so one must be a bit careful with this "upper bound" talk.
>In other words, does the cut-off mass apply only to the deficit >angle, and do boosts still allow me to measure (by non-gravitational >means) arbitrarily large energies (at least in the classical theory)?There's some sense in which energy-momenta can be arbitrarily large. That's because the space of energy-momenta, namely SO(2,1), is noncompact. Maybe you can figure out some more intuitive way to express this.
I was sitting in a chair in the patent office in Bern when all of a sudden a thought occurred to me. If a person falls freely, he will not feel his own weight. - Albert Einstein
© 2006 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|