March 28, 2007

This Week's Finds in Mathematical Physics (Week 248)

John Baez

This week I'll continue the Tale of Groupoidification. But first: some new views of the Sun!

Here's a cool movie of the Moon passing in front of the Sun, as viewed from the "STEREO B" spacecraft. Click on it:

2) Astronomy Picture of the Day, March 3 2007, Lunar transit from STEREO, http://antwrp.gsfc.nasa.gov/apod/ap070303.html

As the name hints, there's a pair of STEREO satellites in orbit around the Sun. One is leading the Earth a little, the other lagging behind a bit, to provide a stereoscopic view of coronal mass ejections.

What's a "coronal mass ejection"? It's an event where the Sun shoots off a blob of ionized gas - billions of tons of it - at speeds around 1000 kilometers per second!

That sounds cataclysmic... but it happens between once a day and 5-6 times a day, depending on where we are in the 11-year solar cycle, also known as the "sunspot cycle". Right now we're near the minimum of this cycle. Near the maximum, coronal mass ejections can really screw up communication systems here on Earth. For example, in 1998 a big one seems to have knocked out a communication satellite called Galaxy 4, causing 45 million people in the US to lose their telephone pager service:

3) Gordon Holman and Sarah Benedict, Solar Flare Theory: Coronal mass ejections, solar flares, and the Earth-Sun connection, http://www.agu.org/sci_soc/articles/eisbaker.html

So, it's not only fun but also practical to understand coronal mass ejections. Here's a movie of one taken by the Solar and Heliospheric observatory (SOHO):

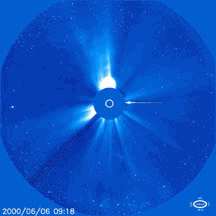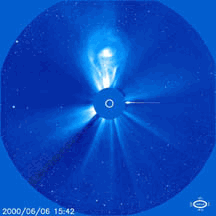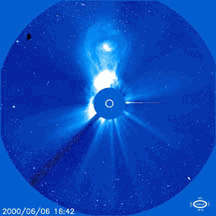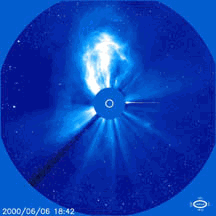
4) NASA, Cannibal coronal mass ejections, http://science.nasa.gov/headlines/y2001/ast27mar_1.htm

As I mentioned in "week150", SOHO is a satellite orbiting the Sun right in front of the Earth, at an unstable equilibrium - a "Lagrange point" - called L1. SOHO is bristling with detectors and telescopes of all sorts, and this movie was taken by a coronagraph, which is a telescope specially designed to block out the Sun's disk and see the fainter corona.

If a coronal mass ejection hits the Earth, it does something like this:

5) NASA, What is a CME?, http://www.nasa.gov/mpg/111836main_what_is_a_cme_NASA%20WebV_1.mpg

In this artist's depiction you can see the plasma shoot off from the Sun, hit the Earth's magnetic field - this actually takes one to five days - and squash it, pushing field lines around to the back side of the Earth. When the magnetic field lines reconnect in back, trillions of watts of power come cascading down through the upper atmosphere, producing auroras. Here's a nice movie of what those can look like:

6) YouTube, Aurora (Northern Lights), http://www.youtube.com/watch?v=qIXs6Sh0DKs

I wish I understood this magnetic field line trickery better! Magnetohydrodynamics - the interactions between electromagnetic fields and plasma - is a branch of physics that always gave me the shivers. The Navier-Stokes equations describing fluid flow are bad enough - if you can prove they have solutions, you'll win $1,000,000 from the Clay Mathematics Institute. Throw in Maxwell's equations and you get a real witches' brew of strange phenomena.

In fact, this subject is puzzling even to experts. For example, why is the Sun's upper atmosphere - the corona - so hot? Here's a picture of the Sun in X-rays taken by another satellite:

7) Transition Region and Coronal Explorer (TRACE), Images of the sun, http://trace.lmsal.com/POD/TRACEpodarchive26.html

This lets you see plasma in the corona with temperatures between 1 million kelvin (shown as blue) and 2 million kelvin (red). By comparison, the visible surface of the Sun is a mere 5800 kelvin!

Where does the energy come from to heat the corona? There are lots of competing theories. It could even be due to "magnetic field reconnection", the same topological phenomenon that triggers auroras when coronal mass ejections smash into the Earth's magnetic field, as in that movie above. For more, try this:

8) Andrew L. Haynes, Clare E. Parnell, Klaus Galsgaard and Eric R. Priest, Magnetohydrodynamic evolution of magnetic skeletons, Proc. Roy. Soc. Lond. A 463 (2007) 1097-1115. Also available as astro-ph/0702604.

A new satellite called Hinode is getting a good look at what's going on, and it seems the magnetic field on the Sun's surface is much more dynamic than before thought:

9) NASA, Hinode: investigating the Sun's magnetic field, http://www.nasa.gov/mission_pages/solar-b/

In fact, weather on the Sun may be more complex than on the Earth. There's "rain" when plasma from the corona cools and falls back down to the Sun's surface... and sometimes there are even tornados! You think tornados on Earth are scary? Check out this movie made during an 8-hour period in August 2000, near the height of the solar cycle:

10) TRACE, Tornados and fountains in a filament on 2 Aug. 2000, movie 13, http://trace.lmsal.com/POD/

Besides the tornados, near the end you can see glowing filaments of plasma following magnetic field lines!

Now for something simpler: the Tale of Groupoidification.

I don't want this to be accessible only to experts, since a bunch of it is so wonderfully elementary. So, I'm going to proceed rather slowly. This may make the experts impatient, so near the end I'll zip ahead and sketch out a bit of the big picture.

Last time I introduced spans of sets. A span of sets is just a set S equipped with functions to X and Y:

                     S
                    / \
                   /   \
                 F/     \G
                 /       \
                v         v 
               X           Y

Have you heard how computer scientists use the term "witness"? They say the number 17 is a "witness" to the fact that the number 221 isn't prime, since 17 evenly divides 221.

That's the idea here. Given a span S as above, we can say an element x of X and an element y of Y are "related" if there's an element s of S with

F(s) = x and G(s) = y

The element s is a "witness" to the relation.

Last week, I gave an example where a Frenchman x and an Englishwoman y were related if they were both the favorites of some Russian s.

Note: there's more information in the span than the relation it determines. The relation either holds or fails to hold. The span does more: it provides a set of "witnesses". The relation holds if this set of witnesses is nonempty, and fails to hold if it's empty.

At least, that's how mathematicians think. When I got married last month, I discovered the state of California demands two witnesses attend the ceremony and sign the application for a marriage license. Here the relation is "being married", and the witnesses attest to that relation - but for the state, one witness is not enough to prove that the relation holds! They're using a more cautious form of logic.

To get the really interesting math to show up, we need to look at other examples of "witnessed relations" - not involving Russians or marriages, but geometry and symmetry.

For example, suppose we're doing 3-dimensional geometry. There's a relation "the point x and the line y lie on a plane", but it's pretty dull, since it's always true. More interesting is the witnessed relation "the point x and the line y lie on the plane z". The reason is that sometimes there will be just one plane containing a point and a line, but when the point lies on the line, there will be lots.

To think of this "witnessed relation" as a span

                     S
                    / \
                   /   \
                 F/     \G
                 /       \
                v         v 
               X           Y

Can we take S to be the set of planes? No! Then there would be no way to define the functions F and G, because the same plane contains lots of different points and lines. So, we should take S to be the set of triples (x,y,z) where x is a point, y is a line, and z is a plane containing x and y. Then we can take

F(x,y,z) = x

and

G(x,y,z) = y

A "witness" to the fact that x and y lie on a plane is not just a plane containing them, but the entire triple.

(If you're really paying attention, you'll have noticed that we need to play the same trick in the example of witnesses to a marriage.)

Spans like this play a big role in "incidence geometry". There are lots of flavors of incidence geometry, with "projective geometry" being the most famous. But, a common feature is that we always have various kinds of "figures" - like points, lines, planes, and so on. And, we have various kinds of "incidence relations" involving these figures. But to really understand incidence geometry, we need to go beyond relations and use spans of sets.

Actually, we need to go beyond spans of sets and use spans of groupoids! The reason is that incidence geometries usually have interesting symmetries, and a groupoid is like a "set with symmetries". For example, consider lines in 3-dimensional space. These form a set, but there are also symmetries of 3-dimensional space mapping one line to another. To take these into account we need a richer structure: a groupoid!

Here's the formal definition: a groupoid consists of a set of "objects", and for any objects x and y, a set of "morphisms"

f: x → y

which we think of as symmetries taking x to y. We can compose a morphism f: x → y and a morphism g: y → z to get a morphism fg: x → z. We think of fg as the result of doing first f and then g. So, we demand the associative law

(fg)h = f(gh)

whenever either side is well-defined. We also demand that every object x has an identity morphism

1_x: x → x

We think of this as the symmetry that doesn't do anything to x. So, given any morphism f: x → y, we demand that

f 1_y = f = 1_x f

So far this is the definition of a "category". What makes it a "groupoid" is that every morphism f: x → y has an "inverse"

f ^-1: y → x

with the property that

f f ^-1 = 1_x

and

f ^-1 f = 1_y

In other words, we can "undo" any symmetry.

So, in our spans from incidence geometry:

                     S
                    / \
                   /   \
                 F/     \G
                 /       \
                v         v 
               X           Y

What's a functor? Given groupoids A and B, clearly a functor

F: A → B

should send any object x in A to an object F(x) in B. But also, it should send any morphism in A:

f: x → y

to a morphism in B:

F(f): F(x) → F(y)

And, it should preserve all the structure that a groupoid has, namely composition:

F(fg) = F(f) F(g)

and identities:

F(1_x) = 1_F(x)

It then automatically preserves inverses too:

F(f ^-1) = F(f) ^-1

Given this, what's the meaning of a span of groupoids? You could say it's a "invariant" witnessed relation - that is, a relation with witnesses that's preserved by the symmetries at hand. These are the very essence of incidence geometry. For example, if we have a point and a line lying on a plane, we can rotate the whole picture and get a new point and a new line lying on a new plane. Indeed, a "symmetry" in incidence geometry is precisely something that preserves all such "incidence relations".

For those of you not comfy with groupoids, let's see how this actually works. Suppose we have a span of groupoids:

                     S
                    / \
                   /   \
                 F/     \G
                 /       \
                v         v 
               X           Y

F(s) = x and G(s) = y

Also suppose we have a symmetry sending s to some other object of S:

f: s → s'

This gives morphisms

F(f): F(s) → F(s')

in X and

G(f): G(s) → G(s')

in Y. And if we define

F(s') = x' and G(s') = y'

we see that s' is a witness to the fact that x' and y' are related.

Let me summarize the Tale so far:

• Spans of groupoids describe "invariant witnessed relations".
• Invariant witnessed relations are the essence of incidence geometry.
• There's a way to turn spans of groupoids into matrices of numbers, so that multiplying matrices corresponds to some nice way of "composing" spans of groupoids (which I haven't really explained yet).

From all this, you should begin to vaguely see that starting from any sort of incidence geometry, we should be able to get a bunch of matrices. Facts about incidence geometry will give facts about linear algebra!

"Groupoidification" is an attempt to reverse-engineer this process. We will discover that lots of famous facts about linear algebra are secretly facts about incidence geometry!

To prepare for what's to come, the maniacally diligent reader might like to review "week178", "week180", "week181", "week186" and "week187", where I explained how any Dynkin diagram gives rise to a flavor of incidence geometry. For example, the simplest-looking Dynkin diagrams, the A_n series, like this for n = 3:

                           o------o------o
                        points  lines  planes      

(There will also be other ways to get spans of groupoids, that don't quite fit into what's customarily called "incidence geometry", but still fit very nicely into our Tale. For example, Dynkin diagrams become "quivers" when we give each edge a direction, and the "groupoid of representations of a quiver" gives rise to linear-algebraic structures related to a quantum group. In fact, I already mentioned this in item E of "week230". Eventually this will let us groupoidify the whole theory of quantum groups! But, I don't want to rush into that, since it makes more sense when put in the right context.)

By the way, some of you have already pointed out how unfortunate it is that last Week was devoted to E₈, instead of this one. Sorry.

Addendum: I thank logopetria for catching typos. For more discussion, go to the n-Category Café.

© 2007 John Baez
baez@math.removethis.ucr.andthis.edu