2.3.3 Electroweak Symmetry Breaking

In the Standard Model, electromagnetism and the weak force are unified into the electroweak force. This is a ${\rm U}(1) \times {\rm SU}(2)$ gauge theory, and without saying so, we just told you all about it in sections 2.3.1 and 2.3.2. The fermions live in representations of hypercharge ${\rm U}(1)$ and weak isospin ${\rm SU}(2)$, exactly as we described in those sections, and we tensor these together to get representations of ${\rm U}(1) \times {\rm SU}(2)$:

The First Generation of Fermions -- ${\rm U}(1) \times {\rm SU}(2)$ Representations
Name	Symbol	$Y$	$I_3$	${\rm U}(1) \times {\rm SU}(2)$ rep
Left-handed leptons	$\left( \! \begin{array}{c} \nu_L \\ e^-_L \end{array} \! \right)$	$-1$	$\pm \frac{1}{2}$	${\mathbb{C}}_{-1} \otimes {\mathbb{C}}^2$
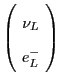Left-handed quarks	$\left( \! \begin{array}{c} u_L \\ d_L \end{array} \! \right)$	$\frac{1}{3}$	$\pm \frac{1}{2}$	${\mathbb{C}}_{\frac{1}{3}} \otimes {\mathbb{C}}^2$
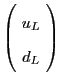Right-handed neutrino	$\nu_R$	$0$	$0$	${\mathbb{C}}_{0} \otimes {\mathbb{C}}$
Right-handed electron	$e^-_R$	$-2$	$0$	${\mathbb{C}}_{-2} \otimes {\mathbb{C}}$
Right-handed up quark	$u_R$	$\frac{4}{3}$	$0$	${\mathbb{C}}_{\frac{4}{3}} \otimes {\mathbb{C}}$
Right-handed down quark	$d_R$	$-\frac{2}{3}$	$0$	${\mathbb{C}}_{-\frac{2}{3}} \otimes {\mathbb{C}}$

These fermions interact by exchanging $B$ and $W$ bosons, which span ${\mathbb{C}} \oplus \sl (2, {\mathbb{C}})$, the complexified adjoint representation of ${\rm U}(1) \times {\rm SU}(2)$.

Yet despite the electroweak unification, electromagnetism and the weak force are very different at low energies, including most interactions in the everyday world. Electromagnetism is a force of infinite range that we can describe by a ${\rm U}(1)$ gauge theory, with the photon as gauge boson. The photon lives in ${\mathbb{C}} \oplus \sl (2, {\mathbb{C}})$, alongside the $B$ and $W$ bosons. It is given by a linear combination

$$\gamma = W^0 + B/2$$

that parallels the Gell-Mann-Nishijima formula, $Q = I_3 + Y/2$. The weak force is of very short range and mediated by the $W$ and $Z$ bosons. The $Z$ boson lives in ${\mathbb{C}} \oplus \sl (2, {\mathbb{C}})$, and is given by the linear combination

$$Z = W^0 - B/2$$

which is in some sense `perpendicular' to the photon. So, we can expand our chart of gauge bosons to include a basis for all of ${\mathbb{C}} \oplus \sl (2, {\mathbb{C}})$ as follows:

Gauge Bosons (second try)
Force	Gauge boson	Symbol
Electromagnetism	Photon	$\gamma$
Weak force	$W$ and $Z$ bosons	$W^+$, $W^-$ and $Z$

What makes the photon (and electromagnetism) so different from the $W$ and $Z$ bosons (and the weak force)? It is symmetry breaking. Symmetry breaking allows the full electroweak ${\rm U}(1) \times {\rm SU}(2)$ symmetry group to be hidden away at high energy, replaced with the electromagnetic subgroup ${\rm U}(1)$ at lower energies. This electromagnetic ${\rm U}(1)$ is not the obvious factor of ${\rm U}(1)$ given by ${\rm U}(1) \times 1$. It is another copy, one which wraps around inside ${\rm U}(1) \times {\rm SU}(2)$ in a manner given by the Gell-Mann-Nishijima formula.

The dynamics behind symmetry breaking are beyond the scope of this paper. We will just mention that, in the Standard Model, electroweak symmetry breaking is believed to be due to the `Higgs mechanism'. In this mechanism, all particles in the Standard Model, including the photon and the $W$ and $Z$ bosons, interact with a particle called the `Higgs boson', and it is their differing interactions with this particle that makes them appear so different at low energies.

The Higgs boson has yet to be observed, and remains one of the most mysterious parts of the Standard Model. As of this writing, the Large Hadron Collider at CERN is beginning operations; searching for the Higgs boson is one of its primary aims.

For the details on symmetry breaking and the Higgs mechanism, which is essential to understanding the Standard Model, see Huang [17]. For a quick overview, see Zee [40].