4 Conclusion

We have studied three different grand unified theories: the ${\rm SU}(5)$, ${\rm Spin}(4) \times {\rm Spin}(6)$ and ${\rm Spin}(10)$ theories. The ${\rm SU}(5)$ and ${\rm Spin}(4) \times {\rm Spin}(6)$ theories were based on different visions about how to extend the Standard Model. However, we saw that both of these theories can be extended to the ${\rm Spin}(10)$ theory, which therefore unites these visions.

The ${\rm SU}(5)$ theory is all about treating isospin and color on an equal footing: it combines the two isospins of ${\mathbb{C}}^2$ with the three colors of ${\mathbb{C}}^3$, and posits an ${\rm SU}(5)$ symmetry acting on the resulting ${\mathbb{C}}^5$. The particles and antiparticles in a single generation of fermions are described by vectors in $\Lambda {\mathbb{C}}^5$. So, we can describe each of these particles and antiparticles by a binary code indicating the presence or absence of up, down, red, green and blue.

In doing so, the ${\rm SU}(5)$ theory introduces unexpected relationships between matter and antimatter. The irreducible representations of ${\rm SU}(5)$

$$\Lambda ^0 {\mathbb{C}}^5 \oplus \Lambda ^1 {\mathbb{C}}^5 \o... ...lus \Lambda ^4 {\mathbb{C}}^5 \oplus \Lambda ^5 {\mathbb{C}}^5$$

unify some particles we normally consider to be `matter' with some we normally consider `antimatter', as in

$$\Lambda ^1 {\mathbb{C}}^5 \cong \left\langle \! \begin{array}... ...nu}_R \end{array} \! \right\rangle \oplus \langle d_R \rangle.$$

In the Standard Model representation, we can think of the matter-antimatter distinction as a ${\mathbb{Z}}_2$-grading, because the Standard Model representation $F \oplus F^*$ splits into $F$ and $F^*$. By failing to respect this grading, the ${\rm SU}(5)$ symmetry group fails to preserve the usual distinction between matter and antimatter.

But the Standard Model has another ${\mathbb{Z}}_2$-grading that ${\rm SU}(5)$ does respect. This is the distinction between left- and right-handedness. Remember, the left-handed particles and antiparticles live in the even grades:

$$\Lambda^{\rm ev}{\mathbb{C}}^5 \cong \langle \overline{\nu}_L... ...{array} \! \right\rangle \oplus \langle \overline{d}_L \rangle$$

while the right-handed ones live in the odd grades:

$$\Lambda^{\rm odd}{\mathbb{C}}^5 \cong \langle \nu_R \rangle \... ...nu}_R \end{array} \! \right\rangle \oplus \langle d_R \rangle.$$

The action of ${\rm SU}(5)$ automatically preserves this ${\mathbb{Z}}_2$-grading, because it comes from the ${\mathbb{Z}}$-grading on $\Lambda {\mathbb{C}}^5$, which ${\rm SU}(5)$ already respects.

This characteristic of the ${\rm SU}(5)$ theory lives on in its extension to ${\rm Spin}(10)$. There, the distinction between left and right is the only distinction among particles and antiparticles that ${\rm Spin}(10)$ knows about, because $\Lambda^{\rm ev}{\mathbb{C}}^5$ and $\Lambda^{\rm odd}{\mathbb{C}}^5$ are irreducible. This says the ${\rm Spin}(10)$ theory unifies all left-handed particles and antiparticles, and all right-handed particles and antiparticles.

In contrast, the ${\rm Spin}(4) \times {\rm Spin}(6)$ theory was all about adding a fourth `color', $w$, to represent leptons, and restoring a kind of symmetry between left and right by introducing a right-handed ${\rm SU}(2)$ that treats right-handed particles like the left-handed ${\rm SU}(2)$ treats left-handed particles.

Unlike the ${\rm SU}(5)$ theory, the ${\rm Spin}(4) \times {\rm Spin}(6)$ theory respects both ${\mathbb{Z}}_2$-gradings in the Standard Model: the matter-antimatter grading, and the right-left grading. The reason is that ${\rm Spin}(4) \times {\rm Spin}(6)$ respects the ${\mathbb{Z}}_2 \times {\mathbb{Z}}_2$-grading on $\Lambda {\mathbb{C}}^2 \otimes \Lambda {\mathbb{C}}^3$, and we have:

$$\begin{array}{ccccc} F_L & \;\cong \; & \Lambda^{\rm odd}{\... ...b{C}}^2 & \otimes & \Lambda^{\rm ev}{\mathbb{C}}^3 \end{array}$$

Moreover, the matter-antimatter grading and the right-left grading are all that ${\rm Spin}(4) \times {\rm Spin}(6)$ respects, since each of the four spaces listed is an irrep of this group.

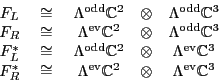
When we extend ${\rm Spin}(4) \times {\rm Spin}(6)$ to the ${\rm Spin}(10)$ theory, we identify $\Lambda {\mathbb{C}}^2 \otimes \Lambda {\mathbb{C}}^3$ with $\Lambda {\mathbb{C}}^5$. Then the ${\mathbb{Z}}_2 \times {\mathbb{Z}}_2$-grading on $\Lambda {\mathbb{C}}^2 \otimes \Lambda {\mathbb{C}}^3$ gives the ${\mathbb{Z}}_2$-grading on $\Lambda {\mathbb{C}}^5$ using addition in ${\mathbb{Z}}_2$. This sounds rather technical, but it is as simple as ``even + odd = odd'':

$$\Lambda^{\rm odd}{\mathbb{C}}^5 \quad \cong \quad \left(\Lam... ...m ev}{\mathbb{C}}^3 \right) \quad \cong \quad F_R \oplus F_L^*$$

and ``odd + odd = even'', ``even + even = even'':

$$\Lambda^{\rm ev}{\mathbb{C}}^5 \quad \cong \quad \left(\Lambd... ... ev}{\mathbb{C}}^3\right) \quad \cong \quad F_L \oplus F_R^* .$$

Recall that $F_R \oplus F_L^*$ consists of all the fermions and antifermions that are right-handed, while $F_L \oplus F_R^*$ consists of the left-handed ones.

Furthermore, the two routes to the ${\rm Spin}(10)$ theory that we have described, one going through ${\rm SU}(5)$ and the other through ${\rm Spin}(4) \times {\rm Spin}(6)$, are compatible. In other words, this cube commutes:

$$\xymatrix{ & {G_{\mbox{\rm SM}}}\ar[rr]^\phi \ar[dl]_\theta ... ...r[rr]^-{{\rm U}(g)} & & {\rm U}(\Lambda {\mathbb C}^5) & \\ }$$

So, all four theories fit together in an elegant algebraic pattern. What this means for physics--if anything--remains unknown. Yet we cannot resist feeling that it means something, and we cannot resist venturing a guess: the Standard Model is exactly the theory that reconciles the visions built into the ${\rm SU}(5)$ and ${\rm Spin}(4) \times {\rm Spin}(6)$ theories.

What this might mean is not yet precise, but since all these theories involve symmetries and representations, the `reconciliation' must take place at both those levels--and we can see this in a precise way. First, at the level of symmetries, our Lie groups are related by the commutative square of homomorphisms:

$$\xymatrix{ {G_{\mbox{\rm SM}}}\ar[r]^\phi \ar[d]_\theta & {\... ... Spin}(4) \times {\rm Spin}(6) \ar[r]^-\eta & {\rm Spin}(10) }$$

Because this commutes, the image of ${G_{\mbox{\rm SM}}}$ lies in the intersection of the images of ${\rm Spin}(4) \times {\rm Spin}(6)$ and ${\rm SU}(5)$ inside ${\rm Spin}(10)$. But we claim it is precisely that intersection!

To see this, first recall that the image of a group under a homomorphism is just the quotient group formed by modding out the kernel of that homomorphism. If we do this for each of our homomorphisms above, we get a commutative square of inclusions:

$$\xymatrix{ {G_{\mbox{\rm SM}}}/{\mathbb Z}_6 \ar@{^{(}->}[r]... ...pin}(6)}{{\mathbb Z}_2} \ar@{^{(}->}[r] & {\rm Spin}(10) \\ }$$

This implies that

$${G_{\mbox{\rm SM}}}/{\mathbb{Z}}_6 \subseteq {\rm SU}(5) \cap... ...ac{{\rm Spin}(4) \times {\rm Spin}(6)}{{\mathbb{Z}}_2} \right)$$

as subgroups of ${\rm Spin}(10)$. To make good on our claim, we must show these subgroups are equal:

$${G_{\mbox{\rm SM}}}/{\mathbb{Z}}_6 = {\rm SU}(5) \cap \left(... ...{{\rm Spin}(4) \times {\rm Spin}(6)}{{\mathbb{Z}}_2} \right) .$$

In other words, our commutative square of inclusions is a `pullback square'.

As a step towards showing this, first consider what happens when we pass from the spin groups to the rotation groups. We can accomplish this by modding out by an additional ${\mathbb{Z}}_2$ above. We get another commutative square of inclusions:

$$\xymatrix{ {G_{\mbox{\rm SM}}}/{\mathbb Z}_6 \ar@{^{(}->}[r]... ...SO}(4) \times {\rm SO}(6) \ar@{^{(}->}[r] & {\rm SO}(10) \\ }$$

Here the reader may wonder why we could quotient $({\rm Spin}(4) \times {\rm Spin}(6))/{\mathbb{Z}}_2$ and ${\rm Spin}(10)$ by ${\mathbb{Z}}_2$ without having to do the same for their respective subgroups, ${G_{\mbox{\rm SM}}}/{\mathbb{Z}}_6$ and ${\rm SU}(5)$. It is because ${\mathbb{Z}}_2$ intersects both of those subgroups trivially. We can see this for ${\rm SU}(5)$ because we know the inclusion ${\rm SU}(5) \hookrightarrow {\rm Spin}(10)$ is just the lift of the inclusion ${\rm SU}(5) \hookrightarrow {\rm SO}(10)$ to universal covers, so it makes this diagram commute:

$$\xymatrix{ {\rm SU}(5) \ar@{^{(}->}[r] \ar@{^{(}->}[dr] & {\rm Spin}(10) \ar[d]^p \\ & {\rm SO}(10) \\ }$$

But this means that ${\rm SU}(5)$ intersects ${\mathbb{Z}}_2 = \ker p$ in only the identity. The subgroup ${G_{\mbox{\rm SM}}}/{\mathbb{Z}}_6$ therefore intersects ${\mathbb{Z}}_2$ trivially as well.

Now, let us show:

Theorem 8   . ${G_{\mbox{\rm SM}}}/{\mathbb{Z}}_6 = {\rm SU}(5) \cap ( {\rm SO}(4) \times {\rm SO}(6) ) \subseteq {\rm SO}(10).$

Proof. We can prove this in the same manner that we showed, in Section 3.1, that

$${G_{\mbox{\rm SM}}}/{\mathbb{Z}}_6 \cong \S ({\rm U}(2) \times {\rm U}(3)) \subseteq {\rm SU}(5)$$

is precisely the subgroup of ${\rm SU}(5)$ that preserves the $2 + 3$ splitting of ${\mathbb{C}}^5 \cong {\mathbb{C}}^2 \oplus {\mathbb{C}}^3$.

To begin with, the group ${\rm SO}(10)$ is the group of orientation-preserving symmetries of the 10-dimensional real inner product space ${\mathbb{R}}^{10}$. But ${\mathbb{R}}^{10}$ is suspiciously like ${\mathbb{C}}^5$, a 5-dimensional complex inner product space. Indeed, if we forget the complex structure on ${\mathbb{C}}^5$, we get an isomorphism ${\mathbb{C}}^5 \cong {\mathbb{R}}^{10}$, a real inner product space with symmetries ${\rm SO}(10)$. We can consider the subgroup of ${\rm SO}(10)$ that preserves the original complex structure. This is ${\rm U}(5) \subseteq {\rm SO}(10)$. If we further pick a volume form on ${\mathbb{C}}^5$, i.e. a nonzero element of $\Lambda ^5 {\mathbb{C}}^5$, and look at the symmetries fixing that volume form, we get a copy of ${\rm SU}(5) \subseteq {\rm SO}(10)$.

Then we can pick a $2 + 3$ splitting on ${\mathbb{C}}^5 \cong {\mathbb{C}}^2 \oplus {\mathbb{C}}^3$. The subgroup of ${\rm SU}(5)$ that also preserves this is

$$\S ({\rm U}(2) \times {\rm U}(3)) \hookrightarrow {\rm SU}(5) \hookrightarrow {\rm SO}(10).$$

These inclusions form the top and right sides of our square:

$$\xymatrix{ {G_{\mbox{\rm SM}}}/{\mathbb Z}_6 \ar@{^{(}->}[r]... ...SO}(4) \times {\rm SO}(6) \ar@{^{(}->}[r] & {\rm SO}(10) \\ }$$

We can also reverse the order of these processes. Imposing a $2 + 3$ splitting on ${\mathbb{C}}^5$ yields a $4 + 6$ splitting on the underlying real vector space, ${\mathbb{R}}^{10} \cong {\mathbb{R}}^4 \oplus {\mathbb{R}}^6$. The subgroup of ${\rm SO}(10)$ that preserves this splitting is $\S (\O (4) \times \O (6))$: the block diagonal matrices with $4 \times 4$ and $6 \times 6$ orthogonal blocks and overall determinant 1. The connected component of this subgroup is ${\rm SO}(4) \times {\rm SO}(6)$.

The direct summands in ${\mathbb{R}}^4 \oplus {\mathbb{R}}^6$ came from forgetting the complex structure on ${\mathbb{C}}^2 \oplus {\mathbb{C}}^3$. The subgroup of $\S (\O (4) \times \O (6))$ preserving the original complex structure is ${\rm U}(2) \times {\rm U}(3)$, and the subgroup of this that also fixes a volume form on ${\mathbb{C}}^5$ is $\S ({\rm U}(2) \times {\rm U}(3))$. This group is connected, so it must lie entirely in the connected component of the identity, and we get the inclusions:

$$\S ({\rm U}(2) \times {\rm U}(3)) \hookrightarrow {\rm SO}(4) \times {\rm SO}(6) \hookrightarrow {\rm SO}(10).$$

These maps form the left and bottom sides of our square.

It follows that ${G_{\mbox{\rm SM}}}/{\mathbb{Z}}_6$ is precisely the subgroup of ${\rm SO}(10)$ that preserves a complex structure on ${\mathbb{R}}^{10}$, a chosen volume form on the resulting complex vector space, and a $2 + 3$ splitting on this space. But this $2 + 3$ splitting is the same as a compatible $4 + 6$ splitting of ${\mathbb{R}}^{10}$, one in which each summand is a complex vector subspace as well as a real subspace. This means that

$${G_{\mbox{\rm SM}}}/{\mathbb{Z}}_6 = {\rm SU}(5) \cap \S (\O (4) \times \O (6)) \subseteq {\rm SO}(10),$$

and since ${G_{\mbox{\rm SM}}}/{\mathbb{Z}}_6$ is connected,

$${G_{\mbox{\rm SM}}}/{\mathbb{Z}}_6 = {\rm SU}(5) \cap ( {\rm SO}(4) \times {\rm SO}(6) ) \subseteq {\rm SO}(10)$$

as desired. $\sqcap$ $\sqcup$

From this, a little diagram chase proves our earlier claim:

Theorem 9   . ${G_{\mbox{\rm SM}}}/{\mathbb{Z}}_6 = {\rm SU}(5) \cap \left({\rm Spin}(4) \times {\rm Spin}(6)\right)/{\mathbb{Z}}_2 \subseteq {\rm Spin}(10)$.

Proof. By now we have built the following commutative diagram:

$$\xymatrix{ {G_{\mbox{\rm SM}}}/{\mathbb Z}_6 \ar@{^{(}->}[r]... ...SO}(4) \times {\rm SO}(6) \ar@{^{(}->}[r]^-i & {\rm SO}(10) }$$

where both the bottom vertical arrows are two-to-one, but the composite vertical maps $q \tilde{\theta}$ and $p \psi$ are one-to-one. Our previous theorem says that the big square with $q \tilde{\theta}$ and $p \psi$ as vertical sides is a pullback. Now we must show that the upper square is also a pullback. So, suppose we are given $g \in ({\rm Spin}(4) \times {\rm Spin}(6))/{{\mathbb{Z}}_2}$ and $g' \in {\rm SU}(5)$ with

$$\tilde{\eta}(g) = \psi(g').$$

We need to show there exists $x \in {G_{\mbox{\rm SM}}}/{\mathbb{Z}}_6$ such that

$$\tilde{\theta} (x) = g, \qquad \tilde{\phi}(x) = g'.$$

Now, we know that

$$i q (g) = p \tilde{\eta}(g) = p \psi(g')$$

so since the big square is a pullback, there exists $x \in {G_{\mbox{\rm SM}}}/{\mathbb{Z}}_6$ with

$$q \tilde{\theta} (x) = q(g), \qquad \tilde{\phi}(x) = g'.$$

The second equation is half of what we need to show. So, we only need to check that the first equation implies $\tilde{\theta} (x) = g$.

The kernel of $q$ consists of two elements, which we will simply call $\pm 1$. Since $q \tilde{\theta} (x) = q(g)$, we know

$$\pm \tilde{\theta}(x) = g .$$

Since $\tilde{\eta}(g) = \psi(g')$, we thus have

$$\tilde{\eta} (\pm \tilde{\theta}(x)) = \psi(g') = \psi \tilde{\phi}(x) .$$

The one-to-one map $\tilde{\eta}$ sends the kernel of $q$ to the kernel of $p$, which consists of two elements that we may again call $\pm 1$. So, $\pm \tilde{\eta} \tilde{\theta}(x) = \psi \tilde{\phi}(x)$. On the other hand, since the top square commutes we know $\tilde{\eta} \tilde{\theta}(x) = \psi \tilde{\phi}(x)$. Thus the element $\pm 1$ must actually be $1$, so $g = \tilde{\theta}(x)$ as desired. $\sqcap$ $\sqcup$

In short, the Standard Model has precisely the symmetries shared by both the ${\rm SU}(5)$ theory and the ${\rm Spin}(4) \times {\rm Spin}(6)$ theory. Now let us see what this means for the Standard Model representation.

We can `break the symmetry' of the ${\rm Spin}(10)$ theory in two different ways. In the first way, we start by picking the subgroup of ${\rm Spin}(10)$ that preserves the ${\mathbb{Z}}$-grading and volume form in $\Lambda {\mathbb{C}}^5$. This is ${\rm SU}(5)$. Then we pick the subgroup of ${\rm SU}(5)$ that respects the splitting of ${\mathbb{C}}^5$ into ${\mathbb{C}}^2 \oplus {\mathbb{C}}^3$. This subgroup is the Standard Model gauge group, modulo a discrete subgroup, and its representation on $\Lambda {\mathbb{C}}^5$ is the Standard Model representation.

We can draw this symmetry breaking process in the following diagram:

$$\xymatrix{ {G_{\mbox{\rm SM}}}\ar[r]^-\phi \ar[d] & {\rm SU}... ...}} & \ar@{<~}[r]^{\mbox{grading and}}_{\mbox{volume form}} & }$$

The ${\rm SU}(5)$ theory shows up as a `halfway house' here.

We can also break the symmetry of ${\rm Spin}(10)$ in a way that uses the ${\rm Spin}(4) \times {\rm Spin}(6)$ theory as a halfway house. We do essentially the same two steps as before, but in the reverse order! This time we start by picking the subgroup of ${\rm Spin}(10)$ that respects the splitting of ${\mathbb{R}}^{10}$ as ${\mathbb{R}}^4 \oplus {\mathbb{R}}^6$. This subgroup is ${\rm Spin}(4) \times {\rm Spin}(6)$ modulo a discrete subgroup. The two factors in this subgroup act separately on the factors of $\Lambda {\mathbb{C}}^5 \cong \Lambda {\mathbb{C}}^2 \otimes \Lambda {\mathbb{C}}^3$. Then we pick the subgroup of ${\rm Spin}(4) \times {\rm Spin}(6)$ that respects the ${\mathbb{Z}}$-grading and volume form on $\Lambda {\mathbb{C}}^5$. This subgroup is the Standard Model gauge group, modulo a discrete subgroup, and its representation on $\Lambda {\mathbb{C}}^2 \otimes \Lambda {\mathbb{C}}^3$ is the Standard Model representation.

We can draw this alternate symmetry breaking process in the following diagram:

$$\xymatrix{ {G_{\mbox{\rm SM}}}\ar[r]^-\theta \ar[d] & {\rm S... ...d}}_{\mbox{volume form}} & \ar@{<~}[r]^{\mbox{ splitting}} & }$$

Will these tantalizing patterns help us understand physics beyond the Standard Model? Only time will tell.