Next: 2.2.2 Leptons Up: 2.2 The Fundamental Fermions Previous: 2.2 The Fundamental Fermions
In the last section, we learned how Heisenberg unified the proton and neutron into the nucleon, and that Yukawa proposed nucleons interact by exchanging pions. This viewpoint turned out to be at least approximately true, but it was based on the idea that the proton, neutron and pions were all fundamental particles without internal structure, which was not ultimately supported by the evidence.
Protons and neutrons are not fundamental. They are made of particles called
quarks. There are a number of different types of quarks,
called flavors. However, it takes only two
flavors to make protons and neutrons: the up quark, ![]() ,
and the down quark,
,
and the down quark, ![]() . The proton consists of two up
quarks and one down:
. The proton consists of two up
quarks and one down:
| Fundamental Fermions (second try) | |||
| Name | Symbol | Charge | |
| Electron | |||
| Up quark | |||
| Down quark | |||
Yet quarks, fundamental as they are, are never seen in isolation. They are always bunched up into particles like the proton and neutron. This phenomenon is called confinement. It makes the long, convoluted history of how we came to understand quarks, despite the fact that they are never seen, all the more fascinating. Unfortunately, we do not have space for this history here, but it can be found in the books by Crease and Mann [8], Segrè [33], and Pais [25].
It is especially impressive how physicists were able to discover
that each flavor of quark comes in three different states,
called colors: red ![]() , green
, green ![]() ,
and blue
,
and blue ![]() . These `colors' have nothing to do with
actual colors; they are just cute names--though as we shall see,
the names are quite well chosen. Mathematically, all that matters is
that the Hilbert space for a single quark is
. These `colors' have nothing to do with
actual colors; they are just cute names--though as we shall see,
the names are quite well chosen. Mathematically, all that matters is
that the Hilbert space for a single quark is
![]() ; we call the
standard basis vectors
; we call the
standard basis vectors ![]() and
and ![]() . The color symmetry
group
. The color symmetry
group ![]() acts on this Hilbert space in the obvious way, via
its fundamental representation.
acts on this Hilbert space in the obvious way, via
its fundamental representation.
Since both up and down quarks come in three color states, there are
really six kinds of quarks in the matter we see around us.
Three up quarks, spanning a copy of
![]() :
:
How could physicists discover the concept of color, given that quarks
are confined? In fact confinement was the key to this discovery!
Confinement amounts to the following decree: all observed
states must be white, i.e., invariant under the action of
![]() . It turns out that this has many consequences.
. It turns out that this has many consequences.
For starters, this decree implies that we cannot see an individual
quark, because they all transform nontrivially under ![]() .
Nor do we ever see a particle built from two quarks, since
no unit vectors in
.
Nor do we ever see a particle built from two quarks, since
no unit vectors in
![]() are fixed by
are fixed by ![]() . But
we do see particles made of three quarks: namely, nucleons!
This is because there are unit vectors in
. But
we do see particles made of three quarks: namely, nucleons!
This is because there are unit vectors in
So: color is deeply related to confinement. Flavor, on the other hand,
is deeply related to isospin. Indeed, the flavor
![]() is
suspiciously like the isospin
is
suspiciously like the isospin
![]() of the nucleon. We even call the
quark flavors `up' and `down'. This is no accident. The proton and
neutron, which are the two isospin states of the nucleon, differ only
by their flavors, and only the flavor of one quark at that. If one
could interchange
of the nucleon. We even call the
quark flavors `up' and `down'. This is no accident. The proton and
neutron, which are the two isospin states of the nucleon, differ only
by their flavors, and only the flavor of one quark at that. If one
could interchange ![]() and
and ![]() , one could interchange protons and
neutrons.
, one could interchange protons and
neutrons.
Indeed, we can use quarks to explain the isospin symmetry of
Section 2.1. Protons and neutrons are so similar, with
nearly the same mass and strong interactions, because ![]() and
and ![]() quarks are so similar, with nearly the same mass and truly identical
colors.
quarks are so similar, with nearly the same mass and truly identical
colors.
So as in Section 2.1, let ![]() act on the flavor
states
act on the flavor
states
![]() . By analogy with that section, we call this
. By analogy with that section, we call this ![]() the
isospin symmetries of the quark model. Unlike the color symmetries
the
isospin symmetries of the quark model. Unlike the color symmetries
![]() , these symmetries are not exact, because
, these symmetries are not exact, because ![]() and
and ![]() quarks
have different mass and charge. Nevertheless, they are useful.
quarks
have different mass and charge. Nevertheless, they are useful.
The isospin of the proton and neutron then arises from the isospin of
its quarks. Define
![]() and
and
![]() , making
, making ![]() and
and ![]() the isospin up and down states at which their names hint. To
find the
the isospin up and down states at which their names hint. To
find the ![]() of a composite, like a proton or neutron, add the
of a composite, like a proton or neutron, add the ![]() for its constituents. This gives the proton and neutron the right
for its constituents. This gives the proton and neutron the right
![]() :
:
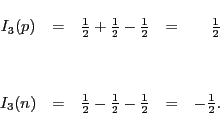
The states
![]() and
and
![]() do not span a copy of the fundamental rep of
do not span a copy of the fundamental rep of ![]() inside
inside
![]() . So, as with color, the equations
. So, as with color, the equations
In physics, the linear combination required to make ![]() and
and ![]() work
also involves the `spin' of the quarks, which lies outside of our
scope. We will content ourselves with showing that it can be
done. That is, we will show that
work
also involves the `spin' of the quarks, which lies outside of our
scope. We will content ourselves with showing that it can be
done. That is, we will show that
![]() really does contain a copy of the fundamental rep
really does contain a copy of the fundamental rep
![]() of
of
![]() . To do this, we use the fact that any rank 2 tensor can be
decomposed into symmetric and antisymmetric parts; for example,
. To do this, we use the fact that any rank 2 tensor can be
decomposed into symmetric and antisymmetric parts; for example,
As a representation of ![]() , we thus have
, we thus have
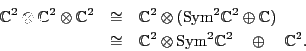
As in the last section, there is no reason to have the full
![]() of isospin
states for nucleons unless there is a way to change protons into neutrons.
There, we discussed how the pions provide this mechanism. The pions live in
of isospin
states for nucleons unless there is a way to change protons into neutrons.
There, we discussed how the pions provide this mechanism. The pions live in
![]() , the complexification of the adjoint representation of
, the complexification of the adjoint representation of
![]() , and this acts on
, and this acts on
![]() :
:
![\includegraphics[scale=0.75]{piN_vertex}](img108.png)
Pions also fit into this model, but they require more explanation, because they are made of quarks and `antiquarks'. To every kind of particle, there is a corresponding antiparticle, which is just like the original particle but with opposite charge and isospin. The antiparticle of a quark is called an antiquark.
In terms of group representations, passing from a particle to its
antiparticle corresponds to taking the dual representation.
Since the quarks live in
![]() , a representation
of
, a representation
of
![]() , the antiquarks live in the dual
representation
, the antiquarks live in the dual
representation
![]() .
Since
.
Since
![]() has basis vectors called up and down:
has basis vectors called up and down:
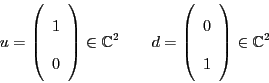
All pions are made from one quark and one
antiquark. The flavor state of the pions must therefore live in
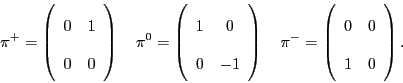
In writing these pions as quarks and antiquarks, we have once again neglected
to write the color, because this works the same way for all pions.
As far as color goes, pions live in
Finally, the Gell-Mann-Nishijima formula also still works for quarks,
provided we define the hypercharge for both quarks to be
![]() :
:
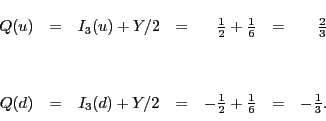
2010-01-11