In his Erlangen Program, Felix Klein advocated the use of group theory to systematize geometry.

In a Dynkin diagram, each dot represents a type of geometrical figure, and each edge represents an incidence relation.

For example, the \(A_3\) diagram describes 3-dimensional projective geometry:

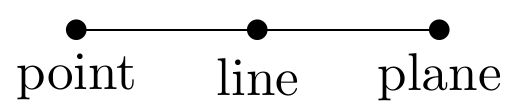
A point can lie on a line, and a line can lie on plane.

The corresponding group is \(\mathrm{SL}(4)\), which acts as symmetries of this geometry.