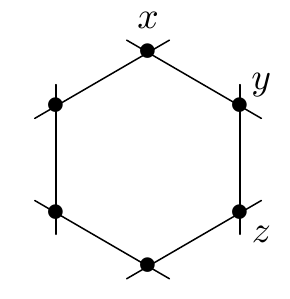
Then:

• A point in \(PC\) is a space \(\langle x \rangle\) spanned by an imaginary split octonion \(x\) with \(x \cdot x = 0\).
• Two points \(\langle x \rangle, \langle y \rangle\) are 'at most one roll away' iff \(x \times y = 0\).
• Two points \(\langle x \rangle, \langle z \rangle\) are 'at most two rolls away' iff \(x \cdot z = 0\).