While there are plenty of things to say about the quantum plane, and
quantum groups, I think I'll home in on my main topic at last:
r-commutative geometry. This is a particular approach to noncommutative
geometry that generalizes what mathematicians and physicists call
"supergeometry". So first I should say a brief word about supergeometry.
First, recall that the plain old geometry of manifolds can be cast into the
language of commutative algebra by considering not the manifold itself as a
set of points, but the algebra of (smooth, complex) functions
on the manifold. (In this language, for example, vector fields are
derivations, vector bundles are projective modules, and so on -- every
geometric construct has an algebraic analog.) Now in the 1970's, physicists
really caught on to the fact that considering only commutative algebras was
horribly unfair to fermions, which like to anticommute: i.e. they have
This turned out to be fascinating (it's a bit premature to say "useful") in particle physics, where it goes by the name of supersymmetry. The idea is that there should be a symmetry between bosons and fermions. While this is not at all observed in nature, it would be nice if it were true, so people have developed clever ways of rigging up their theories so that you never see the "superpartners" every particle has: for the photon, the photino, for the gluon, the gluino, for the leptons, schleptons, for the quarks, squarks... you get the pattern. (Don't complain to me if you think this is silly, it wasn't my idea!) Superstrings are the latest of these "super" ideas in particle physics.
Supersymmetry has actually proven itself in a more practical manner in nuclear physics, where it lets one model resonances in nuclei, relating the properties of fermionic and bosonic nuclei.
Where supergeometry really shines, though, is in mathematics. For example, Ed Witten came up with beautiful proofs of the Atiyah-Singer index theorem and the positive mass theorem (a theorem about general relativity) using supergeometry. (As usual, he left it to others to make his arguments rigorous.)
While I personally don't think that bosons and fermions were created equal in the manner postulated by supersymmetry, I do favor an approach to physics which doesn't take bosons, or commuting variables, to be somehow superior to fermions, or anticommuting variables. This demands supergeometry. For example, a decent treatment of classical fermions requires a supermanifold for the "phase space".
My own personal twist (motivated by the work of many people on anyons, the braid group, quantum groups, etc.) is to try to take a look at what geometry would be like if one wanted to be fair to anyons as well as bosons and fermions. This is "r-commutative geometry."
Recall that given a vector space ![]() , an invertible linear transformation
, an invertible linear transformation
![]() , the Yang-Baxter equations say that
, the Yang-Baxter equations say that
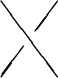
The Yang-Baxter equations say that
![\begin{picture}(198,179)(19,641)
\thicklines\put( 20,820){\line( 2,-3){ 72}}
\pu...
...t(120,732){\makebox(0,0)[lb]{\raisebox{0pt}[0pt][0pt]{\frtnrm =}}}
\end{picture}](img70.gif)
Now suppose that our vector space is really an algebra -- let's call it
![]() . (I mean an associative algebra with unit.) The product in the
algebra defines a multiplication map
. (I mean an associative algebra with unit.) The product in the
algebra defines a multiplication map
![]() , given by
, given by
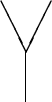
Associativity simply says that ![]() , or in terms of diagrams,
, or in terms of diagrams,
![\begin{picture}(141,81)(31,720)
\thicklines\put( 42,761){\line( 1,-2){ 11}}
\put...
...t( 99,758){\makebox(0,0)[lb]{\raisebox{0pt}[0pt][0pt]{\frtnrm =}}}
\end{picture}](img117.gif)
Now these diagrams aren't really braids because of the "fusion of strands" that's taking place, but they fit in well with the braid group philosophy. For example, there is a sense in which the two trees I've drawn above are topologically the same, just as the Yang-Baxter equation expresses a topological identity. There are generalizations of braids, e.g. the "ribbon graphs" of Reshetikhin and Turaev, that make all this precise.
Now: an "r-algebra" is an algebra ![]() equipped with a solution
equipped with a solution
![]() of the Yang-Baxter equations such that:
of the Yang-Baxter equations such that:
1)
![]() and
and
![]() for all
for all ![]() in
in ![]() -- i.e., one "switches" the identity 1
with
-- i.e., one "switches" the identity 1
with ![]() in the usual manner;
in the usual manner;
2) the following conditions hold -- I'll draw them pictoriallly:
![\begin{picture}(157,101)(21,720)
\thicklines\put(118,820){\line( 1,-2){ 40}}
\pu...
...t( 96,761){\makebox(0,0)[lb]{\raisebox{0pt}[0pt][0pt]{\frtnrm =}}}
\end{picture}](img121.gif)
and
![\begin{picture}(168,102)(14,719)
\thicklines\put(149,766){\line( 3, 5){ 33}}
\pu...
...t( 96,761){\makebox(0,0)[lb]{\raisebox{0pt}[0pt][0pt]{\frtnrm =}}}
\end{picture}](img122.gif)
If you like equations instead of pictures, these are
Now commutativity says that ![]() -- in other words, you can multiply
two elements of
-- in other words, you can multiply
two elements of ![]() , or you can switch them first and then multiply them,
and you'll get the same result. Generalizing this, we say that an
r-algebra is "r-commutative" if
, or you can switch them first and then multiply them,
and you'll get the same result. Generalizing this, we say that an
r-algebra is "r-commutative" if
![\begin{picture}(185,120)(17,699)
\thicklines\put(163,759){\line( 0,-1){ 59}}
\pu...
...t( 93,754){\makebox(0,0)[lb]{\raisebox{0pt}[0pt][0pt]{\frtnrm =}}}
\end{picture}](img131.gif)
In words: "switch, then multiply, equals multiply."
It turns out that one can do a fair amount of geometry for r-commutative algebras. And there are lots of examples of r-commutative algebras. In fact, many of the algebras obtained by quantization are r-commutative: for example, the Clifford algebra, the Weyl algebra, noncommutative tori, the quantum plane (and all other r-symmetric algebras), and quantum groups. Also, all supercommutative algebras are automatically r-commutative.
In fact, I believe that there is a deep relation between braids (or r-commutativity) and quantization. This goes back to Kauffman's observation that the skein relation for the Conway polynomial
![\begin{picture}(223,64)(21,755)
\thicklines\put(211,814){\line( 0,-1){ 59}}
\put...
...t( 72,782){\makebox(0,0)[lb]{\raisebox{0pt}[0pt][0pt]{\frtnrm -}}}
\end{picture}](img132.gif)
and the canonical commutation relations
More later...
© 1992 John Baez
baez@math.removethis.ucr.andthis.edu