

The most amazing thing about this piece of art, titled "Museum of Memories", is that it's produced by a 4096 byte file! It's an entry in the
Revision 2023 4k
Executable Graphics competition by @luna. It contains three prior
4k artworks, compressed.... and more!
April 17, 2023
I'm fascinated by the Inuit languages in Alaska, Canada and Greenland. These languages ring much of the Arctic Ocean! I just learned that they use a base 20 system for numbers, with a 'sub-base' of 5. That is, quantities are counted in scores (twenties) with intermediate numerals for 5, 10, and 15. This makes a lot of sense if you look at your fingers and toes.
But the Inuit didn't have a written form of their number system until the early 1990s, when high school students in the town of Kaktovik, Alaska invented one! There were just nine students at this small school, and they all joined in.
They used 5 principles:
They decided that the symbol for zero should look like crossed arms, meaning that nothing was being counted. So here's what they came up with:
The students built base-20 abacuses. These were initially intended to help the conversion from decimal to base 20 and vice versa, but soon the students started using them to do arithmetic in base 20.
The upper section of their abacus has 3 beads in each column for the values of the sub-base of 5, while the lower section has 4 beads in each column for the remaining units.
The students discovered their new system made arithmetic easier than it was with Arabic numerals. Adding two digits together often gives a result that looks like the combination of the two digits!
The students also found that long division was more fun with Kaktovik numerals! They noticed visually interesting patterns. They discovered that they could keep track of intermediate steps with colored pencils.
And then something interesting happened: after the students of Kaktovik invented their new numerals, their scores on standardized math tests improved dramatically! Before, their average score was down in the 20th percentile. Afterwards, their scores shot up to above the national average.
Some argue that being able to work in both base 10 and base 20 was helpful — much like being bilingual. Another explanation is that having a written system of numbers that matched the local language was helpful.
But I suspect that even more important was the sheer process of developing their own system of numerals! Getting engaged in mathematics is so much better than learning it passively.
But this was just the start of the story. For more, read this:
At first students would convert their assigned math problems into Kaktovik numerals to do calculations, but middle school math classes in Kaktovik began teaching the numerals in equal measure with their Hindu-Arabic counterparts in 1997. Bartley reports that after a year of the students working fluently in both systems, scores on standardized math exams jumped from below the 20th percentile to "significantly above" the national average. And in the meantime, the board of education in the North Slope Borough’s district seat, Utqiagvik, passed a resolution that spread the numerals almost 500 miles along the Arctic coast. The system was even endorsed by the Inuit Circumpolar Council, which represents 180,000 Inuit across Alaska, Canada, Greenland and Russia.But under the federal No Child Left Behind Act, from 2002 to 2015, schools faced severe sanctions—or even closure—for not meeting state standards, provoking a "scare" that some local educators say squeezed the Kaktovik numerals into a marginal role despite the system's demonstrated educational impact. "Today the only place they're really being used is in the Iñupiaq language classrooms," says Chrisann Justice, the North Slope Borough’s Iñupiaq education department specialist. "We’re just blowing on the coal."
Why is Scientific American talking about Kaktovik numerals just now? It's because some linguists working with the Script Encoding Initiative at U.C. Berkeley recently got them added to Unicode! See here:
I read the Wikipedia article about this numeral system and came across this long division example:I suspect there's more to be said. Maybe someone has worked out more details somewhere?My nearly exact thought process while reading the caption:
Article: "The divisor goes into the first two digits of the dividend one time, for a one in the quotient."
Me: "OK, sure, got it."
Article: "It fits into the next two digits (red) once if rotated..."
Me: "What do you mean, "rotated"?"
...
Me: "holy *SHIT*, that's totally genius"
The Kaktovik numerals were invented by high school students who spoke Iñupiaq:
This map also shows other Inuit languages:
1 2 3 #4 5 6 ♭7
and could sing it without much effort on the first try. I seem to be getting better at this sort of thing!
More importantly, it's a really cool scale. Rob van Hal's video explains what it sounds like and what you can do with it:
You can think of it as a blend of the Lydian mode, with its mystical raised 4th:
1 2 3 #4 5 6 7
and the Mixolydian mode, with its lowered 7th:
1 2 3 4 5 6 ♭7
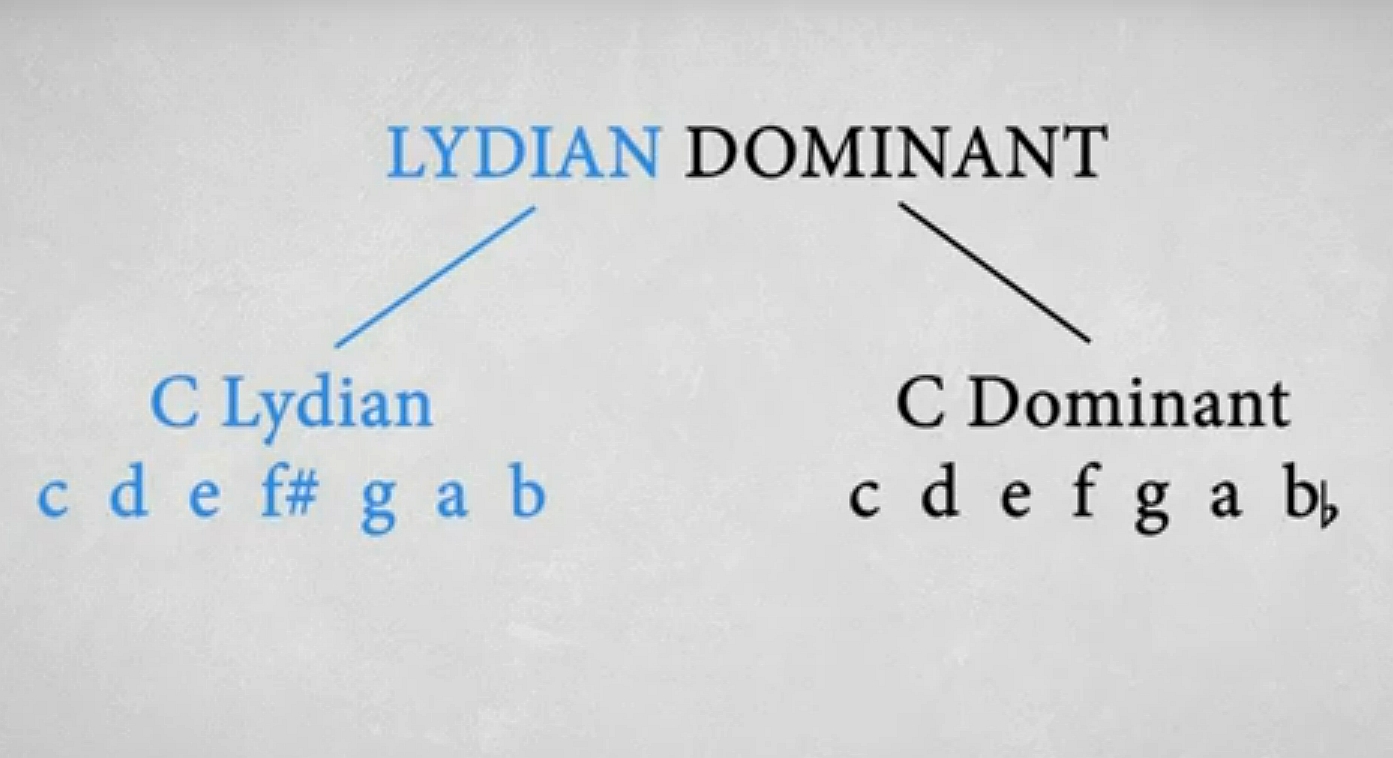
But why does this image from van Hal's video call the Mixolydian mode 'dominant'? Probably because it contains the dominant 7th chord, where we take a major triad and extend it by playing a minor 7th on top:
1 3 5 ♭7
Indeed, you can get all the notes of the Lydian dominant scale from a chord where you stack the triad 2 #4 6 on top of a dominant 7th. Since we're playing them an octave higher, we add seven to 2, #4, and 6 and get this:
1 3 5 ♭7 9 #11 13
This is a nice jazzy chord called a 'dominant 13th sharp 11'. And if you play it in C, musicians might call it a 'C13#11 chord' because the dominant 7th is so prevalent that it's taken for granted in this notation!
But if you play this chord you might leave out the 3 and 5, which are so taken for granted that actually playing them just muddies the chord with unnecessary notes. So you might just play this:
1 ♭7 9 #11 13
There are lots of other ways to play it.
Another way to think about the Lydian dominant scale is that it's the 4th mode of melodic minor ascending. Melodic minor is a scale you play like this when you're going up:
1 2 ♭3 4 5 6 7
If you start it on the 4 you get a Lydian dominant scale. Think about it!
Another name for the Lydian dominant scale is the 'acoustic scale'. This is because you can get approximately get the notes of this scale by playing all the overtones of a single tone... and quitting at the right point. Read this for the details:
To see how people apply the Lydian dominant scale in music, start with van Hal's video. Then take it to the next level by watching Peter Martin and Adam Maness explain how to dominate the Lydian dominant:
For me, watching these guys talk about music is like watching Ed Witten talk about physics. I get bits here and there. It all goes by too fast. Still, it's tremendously exciting!
They describe and illustrate several things you can do in jazz with the Lydian dominant scale. Adam Maness tries to go through topics systematically, from simple to complicated. But Peter Martin — the pianist for Dianne Reeves, and a very cool cat — interrupts and talks about fancier topics, so the end result is a bit disorganized.
Nonetheless I really benefit from hearing actual jazz theory experts talk about this stuff. At the very least, it gives me a useful sense of how crappy I am at music theory, and playing the piano. But not in a depressing way. It makes me want to improve!
If you want do jam in Lydian dominant, you can use this backing track:
If you don't, listening to it is still a good way to absorb the vibe of Lydian dominant. There are tons of backing tracks like this on YouTube.