

No — it's just a halo combined with a full parhelic circle, two sun dogs and a 120° parhelion. They were photographed on a cold foggy day in Finland by Pauli Hänninen.
A parhelic circle is a horizontal white line at the same height from the horizon as the Sun, or occasionally the Moon. If it's 'full', it stretches all around the sky. More commonly it only appears in sections. It happens when beams of sunlight are reflected by vertical or almost vertical hexagonal ice crystals in the atmosphere.
A 120° parhelion appears as a bright blue-white spot on the parhelic circle, 120° away from the Sun. It's caused by light that bounces inside the hexagonal ice crystals at least twice.
A sun dog or 'parhelion' is a bright spot 22° to the left or right of the sun, again caused by ice crystals in the upper atmosphere. Why 22°? I don't really know: all I know is that "these crystals act as prisms, bending the light rays passing through them with a minimum deflection of 22°."
In the above photo you can see a halo around the Sun, which seems to be 22° away... and two sundogs at left and right. Then there's the long parhelic circle. It doesn't show the 120° parhelion, but here's a photo showing that:

For a diagram of how all these events fit together, and more photos, see:
Some famous philosophers have written about sun dogs! In his Meteorology, Aristotle recorded an event where "two mock suns rose with the sun and followed it all through the day until sunset." And some sun dogs seen in Rome in the summer of 1629 made René Descartes interrupt his metaphysical studies and write a work on natural philosophy, called The World.
It's not complicated if you think about it the right way. I never knew this cool fact until last night, when I read this:
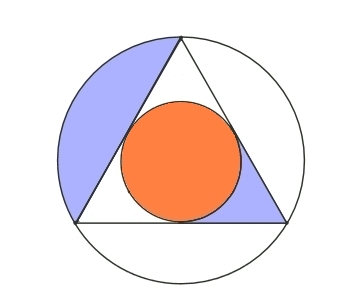
In case you're wondering, this is an equilateral triangle with a small circle inscribed in it and a big circle circumscribed around it.
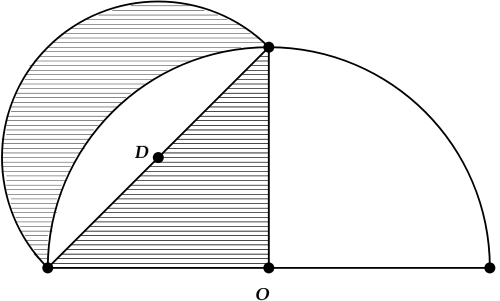
Puzzle: show the crescent has the same area as the triangle.
Greek mathematicians really wanted to 'square the circle': the goal being to use straightedge and compass to first draw a circle and then construct a square with the same area.
In 440 BC, Hippocrates of Chios figured out how to square this crescent-shaped region, which lies between the circle centered at O and the smaller circle centered at D. So, this region is called the lune of Hippocrates.
This gave some people hope that the circle could be squared... but it was a false hope. Much later, around 1885, Lindemann and Weierstrass proved that squaring the circle was impossible.
Any crescent-shaped region formed by two circular arcs is called a lune. It's widely believed that only 5 kinds of lune can be squared. Three were discovered by Hippocrates. Two more were discovered by Martin Johan Wallenius in 1766. A proof that these are the only squarable lunes was given by Tchebatorew and Dorodnow. However, they made some assumptions which require further proof.
For more, try these:
Here's a true story from a spacewalk on July 16 this year:
... As I move back along my route towards the airlock, I become more and more certain that the water is increasing. I feel it covering the sponge on my earphones and I wonder whether I'll lose audio contact. The water has also almost completely covered the front of my visor, sticking to it and obscuring my vision. I realise that to get over one of the antennae on my route I will have to move my body into a vertical position, also in order for my safety cable to rewind normally.At that moment, as I turn 'upside-down', two things happen: the Sun sets, and my ability to see — already compromised by the water — completely vanishes, making my eyes useless; but worse than that, the water covers my nose — a really awful sensation that I make worse by my vain attempts to move the water by shaking my head.
By now, the upper part of the helmet is full of water and I can't even be sure that the next time I breathe I will fill my lungs with air and not liquid. To make matters worse, I realise that I can't even understand which direction I should head in to get back to the airlock. I can't see more than a few centimetres in front of me, not even enough to make out the handles we use to move around the Station.
I try to contact Chris and Shane: I listen as they talk to each other, but their voices are very faint now: I can hardly hear them and they can't hear me. I.m alone. I frantically think of a plan. It.s vital that I get inside as quickly as possible. I know that if I stay where I am, Chris will come and get me, but how much time do I have? It's impossible to know.
Blind, unable to hear, and alone, Luca Parmitano still managed to figure out a solution to get himself back to the airlock. You can watch a movie of it here!
Later, NASA blandly reported:
The water was not an immediate health hazard for Parmitano, but Mission Control decided to end the spacewalk early....
On September 3, 2002, an amateur astronomer named Bill Yeung looked into his telescope and discovered a strange object near Earth. Experts were surprised to discover that it was orbiting Earth! The orbit was unstable, which meant this object hadn't been here long. But there was no recently launched spacecraft that matched the orbit of this thing!
It got the name J002E3. It's fun to watch this animated gif and see how J002E3 came in from the Lagrange point L1 between the Earth and Sun, went around the Earth a few times, and then got kicked out.
But what was it?
University of Arizona astronomers found that its electromagnetic spectrum was consistent with white titanium dioxide paint - the same paint used by NASA for the Saturn V rockets. Tracing back its orbit, they found that it had probably been orbiting the Sun for 31 years. The last time it was near Earth was1971.
This seemed to suggest that it was a part of the Apollo 14 mission. But NASA knew the whereabouts of all hardware used for this mission! The third stage of that rocket, for example, was deliberately crashed into the Moon for seismic studies.
So, the most likely explanation seems to be that J002E3 is the third stage of the rocket for Apollo 12. NASA originally planned to shoot this into an orbit around the Sun. But they used more of the propellant than planned, and it seems that venting the rest didn't give this rocket stage enough energy to escape the Earth.Moon system. So, it ended up in a complicated orbit around the Earth after passing by the Moon on November 18, 1969.
It may hit earth someday! It weighs 10 tonnes. But don't worry: a 10-tonne meteor hits the Earth every few years, and most of them don't cause much trouble.
The explanation here is adapted from Wikipedia, and the animated gif was made by Paul Chodas aand Ron Baalke of NASA.
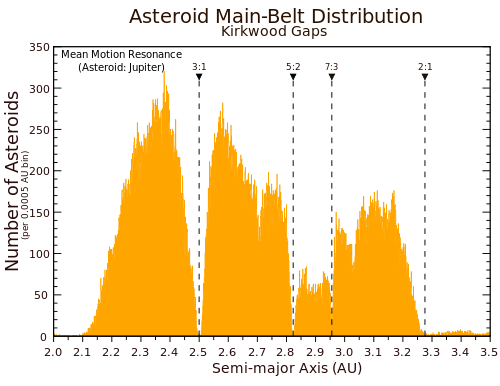
Most asteroids lie between Mars and Jupiter, but they avoid certain places — the Kirkwood gaps, discovered in 1857 by Daniel Kirkwood, a professor at a small college in Pennsylvania. He noticed that not many asteroids go 3 times around the Sun each time Jupiter goes once around the Sun: this is called a 3:1 resonance, and you can see that gap on the chart.
Other gaps show up at other simple ratios. Why does this happen? I don't fully understand it. The usual story is that it's like pushing on a swing: if you push on a swing each time it swings back, it picks up energy and swings higher. Similarly, if you have a big heavy planet orbiting a star, asteroids that go around N times each time the planet goes around M times pick up energy and their orbits change... leaving a gap at this location.
This effect, called an unstable N:M resonance, happens a lot. You can also see it in Saturn's rings, which have gaps where the dust particles would be in resonance with its big moons.
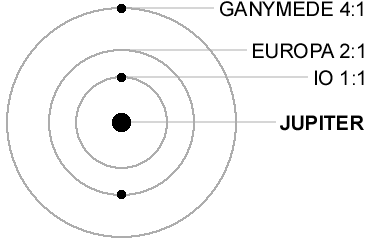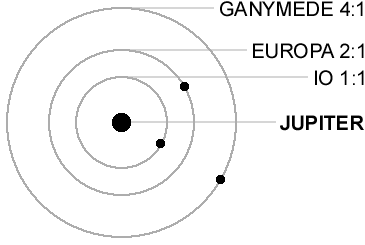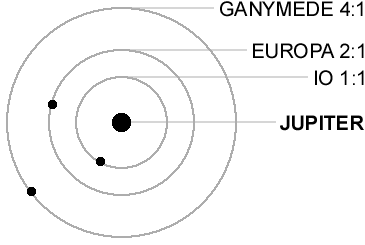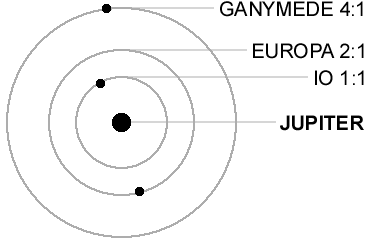
So far, so good. But there are also stable resonances, where one planet or moon likes to go around N times when the other goes around M times! For example Jupiter's moon Io is in a 2:1 resonance with Europa, and Europa is in a 2:1 resonance with Ganymede.
Also, Neptune is in a 3:2 resonance with Pluto.
So sometimes resonance makes orbits unstable, but sometimes it makes them stable. Why? Wikipedia tries to explain it, but I'd need to see some more detail — probably some math — to really understand what makes the difference between the two cases:
Here are the main Kirkwood gaps. It helps to know that the Earth is 1 astronomical unit or AU from the Sun, Mars is 1.52 AU away from the Sun, and Jupiter is 5.2 away. The biggest Kirkwood gaps are these:
Hey! Why are there families of asteroids located in the gaps? Apparently they're in the process of moving out, but I'd like to know more.
There are also lots of weaker or narrower gaps:
If you played sounds at these frequency ratios, you'd get different chords. 2:1 is an octave. 5:3 is a major sixth. 3:1 is an octave and a fifth. So the Kirkwood gaps are a nice example of the 'music of the spheres' that astronomers of old used to dream about. But the music is not played by the asteroids — it's in the gaps!
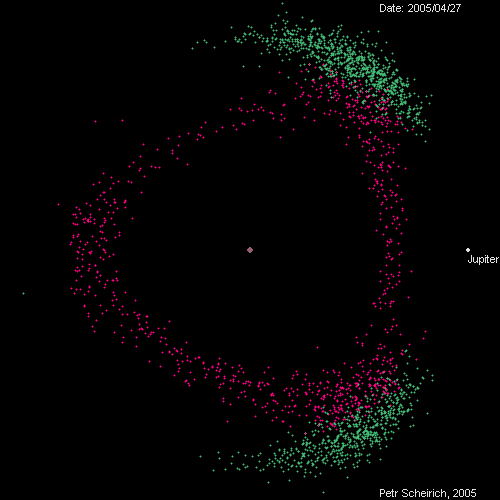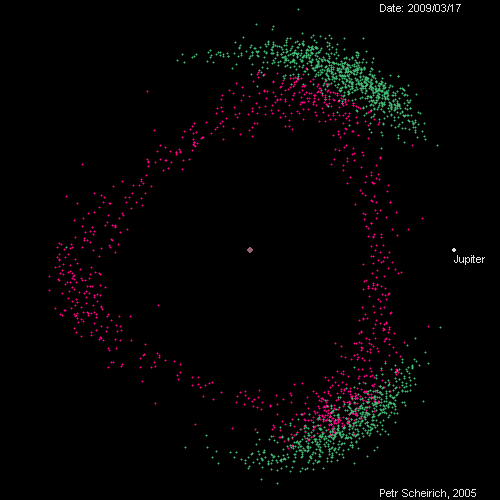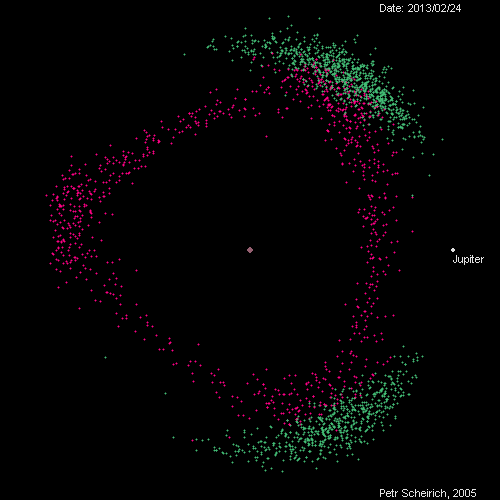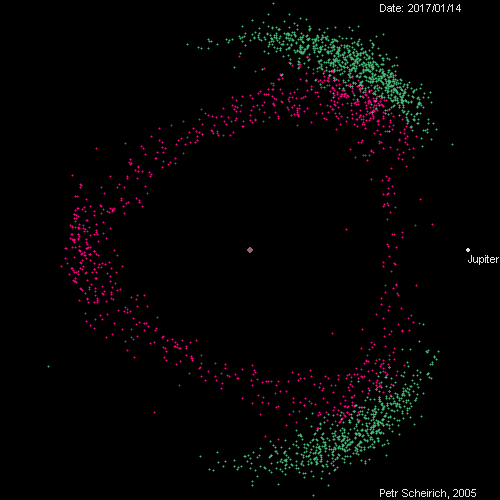
Here are some asteroids viewed in a rotating frame of reference where Jupiter almost stands still. The Trojans, in green, are asteroids that stay near the Lagrange points 600 ahead or behind Jupiter. They go around the Sun once each time Jupiter orbits the Sun. But the Hildas, in purple, go around the Sun 3 times while Jupiter goes around twice. We say they're in a 3:2 resonance with Jupiter.
The Hildas seem to be moving in a triangular pattern. But actually each one takes an elliptical orbit around the Sun. There are three kinds of ellipses. Two go farthest from the Sun near the Lagrange points, while one goes farthest from the Sun opposite Jupiter. Although the whole triangle of Hildas is nearly equilateral, it's not quite. The side between the two Lagrange points is a bit different from the two other sides. You can also see the whole triangle pulsing as Jupiter moves in and out!
This animated gif is one of many made by Petr Scheirich, and you can have hours of fun looking at his website:
There's a lot to say about Trojans and Lagrange points, but let me talk about Hildas. Over 1,100 Hildas have been found, the first being Hilda, named after the discoverer's daughter. It's big — 175 kilometers in diameter — but not very bright, because it's made of ancient stuff containing lots of carbon, similar to the nucleus of a comet.
The Hildas don't form a 'true' asteroid family, because they aren't fragments of a single parent object. Instead, they're a 'dynamical' family: they're defined by having similar orbits. Any Hilda's orbit has an eccentricity less than 0.3, an inclination less than 200, and a semi-major axis between 3.7 AU and 4.2 AU. Remember, the semi-major axis of an ellipse is half the distance between the farthest points.
So, the Hildas are outside the main asteroid belt, which lies between the 4:1 resonance with Jupiter at 2.1 AU and the 2:1 resonance at 3.0 AU.
The density of Hildas near the triangle's corners is more than twice the density on the sides. The reason is that the Hildas move more slowly when they're farther from the Sun! So, they stay near the corners for an average of 5.0-5.5 years, but move along the sides of the triangle more quickly, for 2.5 to 3.0 years. The overall period of the Hildas is about 7.9 years, which is 2/3 the period of Jupiter.
The Yarkovsky drift makes small asteroids move away from the Sun or get closer to it, depending on which way they turn.
The asteroid at left is turning the same way it's revolving around the Sun. So the hottest part of the asteroid, which has been in the sunshine warming up all day, is in back — the part marked "P.M." When it radiates heat, this pushes the asteroid in the direction it's already going, so the asteroid gains energy! This gradually makes the asteroid move farther from the Sun: that's the 'Yarkovsky drift'.
The asteroid at right is turning in the opposite way from how it's revolving around the Sun. So, radiating heat makes this asteroid lose energy and move closer to the Sun.
This effect was discovered theoretically in 1900 by a Russian civil engineer named Ivan Osipovich Yarkovsky, who worked on scientific problems in his spare time. It's a small effect, which is strongest for small asteroids, so it was only seen in the 1990s. For twelve years, astronomers carefully used radar to measure the position of a small asteroid called 6489 Golevka. It drifted 15 kilometers due to this effect!
To understand how small this effect is, think about this. The force it created on 6489 Golenka was about 0.25 newton. This is the force that pushes down on your hand when you're holding a quarter of an apple. It created an acceleration of just a tenth of a nanometer per second per second. But this acceleration adds up over time!
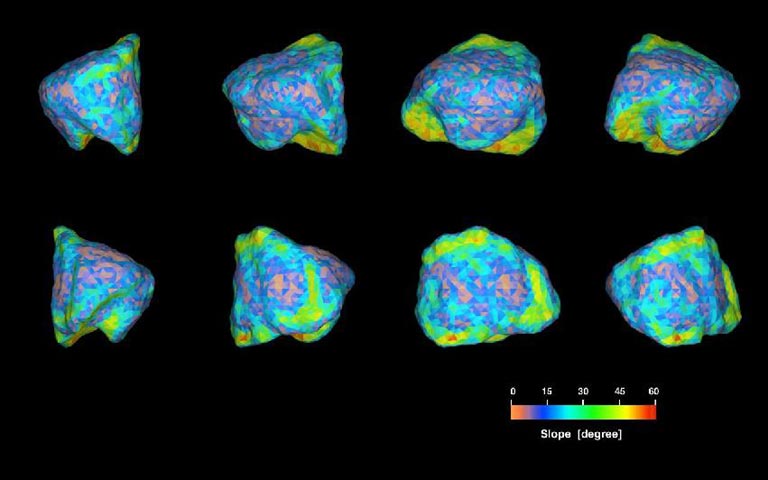
The YORP effect is a way for asteroids to spin faster and faster... even until they explode!
It's powered by sunlight. Sunlight heats the asteroid, which then radiates heat in the form of infrared light. If an asteroid has an irregular shape, like 6489 Golevka here, this infrared light can push on the asteroid in a way that makes it spin!
This is impossible if the asteroid is a sphere or ellipsoid made of some uniform material. It's easiest to understand for an asteroid shaped like a windmill.
Indeed, the YORP effect may remind you of a light mill, or Crookes radiometer — a toy like a windmill in a glass bulb with vanes black on one side, white on the other, powered by light. But it's a bit different, since these light mills only turn the way they do because there's a little gas in the bulb. If the bulb contained a perfect vacuum, the light mill would feel a torque pushing it the opposite way. Light mills are very tricky! Both Maxwell and Einstein wrote papers on them... and they came up with different explanations of how they work! I wrote about this on the n-Category Café once.
The full name of the YORP effect is the Yarkovsky–O'Keefe–Radzievskii–Paddack effect. It's a relative of the Yarkovsky effect, which makes a rotating asteroid move towards or away from the Sun.
In 2007, astronomers detected the YORP effect in a small asteroid named 2000 PH5. To celebrate, they renamed this asteroid 54509 YORP. The rotation rate of this asteroid is increasing by 0.0002 degrees per day each day.
That doesn't sound like much... but in astronomy, things take a long time. The rotation rate of this asteroid will double in 600,000 years. Simulations show that it will keep spinning faster until it turns around once every 20 seconds... and then it will burst! Asteroids are often loosely held together clumps of rock. If they spin fast, they can split into a binary asteroid. So, the YORP effect may explain the existence of some binary asteroids.
According to Wikipedia:
Observations show that asteroids larger than 125 km in diameter have rotation rates that follow a Maxwellian frequency distribution, while smaller asteroids (in the 50 to 125 km size range) show a small excess of fast rotators. The smallest asteroids (size less than 50 km) show a clear excess of very fast and slow rotators, and this becomes even more pronounced as smaller populations are measured. These results suggest that one or more size-dependent mechanisms are depopulating the centre of the spin rate distribution in favour of the extremes. The YORP effect is a prime candidate. It is not capable of significantly modifying the spin rates of large asteroids by itself, however, so a different explanation must be sought for objects such as 253 Mathilde.
(If this images doesn't play as an animated gif, download it and look at it that way.)
About 2 billion years ago, an asteroid about 100 kilometers across was completely pulverized when a smaller one hit it! This created the Koronis family in the outer part of the main asteroid belt. There are hundreds of asteroids in this family. The biggest are Lacrimosa and Urda, with diameters of 48 and 44 kilometers.
In the simulation here, a 119-kilometer asteroid is hit by a smaller one moving at 5 kilometers per second - or roughly 10,000 miles per hour. The shock wave created by the impact shatters the bigger asteroid, which had a lot of cracks to begin with. Hundreds of thousands of fragments shoot in all directions. Then gravity pulls them together over several days. The largest new asteroid, shown here, contains 4% of the mass of its parent.
About 2 billion years ago, an asteroid about 100 kilometers across was completely pulverized when a smaller one hit it! This created the Koronis family in the outer part of the main asteroid belt. There are hundreds of asteroids in this family. The biggest are Lacrimosa and Urda, with diameters of 48 and 44 kilometers.
In the simulation here, a 119-kilometer asteroid is hit by a smaller one moving at 5 kilometers per second — or roughly 10,000 miles per hour. The shock wave created by the impact shatters the bigger asteroid, which had a lot of cracks to begin with. Hundreds of thousands of fragments shoot in all directions. Then gravity pulls them together over several days. The largest new asteroid, shown here, contains 4% of the mass of its parent.
This simulation was one of many done by Patrick Michel around 2000. He used a Compaq Dec Alpha and a Beowulf cluster. To compute the gravitational interaction of many chunks of rock using parallel processing, he used the "hierarchical tree method".

You are in a helicopter exploring the southern part of Mars. When you enter Newton Crater, you see dark streaks that look like signs of dripping water, or moisture. What are they?
Here's what we know. They are 0.5 to 5 meters wide. They appear in the early spring. They grow larger in the summer. They go away in the winter. Similar things appear in a number of places in the southern hemisphere, but so far none have been seen in the north.
A paper in Science argues that they could be caused by brine — very salty water. Salts absorb water very eagerly, and brine has a lower melting point than ordinary water.
This image was created using a photo made on 30 May 2011 by the High Resolution Imaging Science Experiment (HiRISE) camera on NASA's Mars Reconnaissance Orbiter. It has been reprojected to show what this view would look like from a helicopter inside the crater. A synthetic Mars-like sky has been added, and the color has been enhanced. The season was summer at the location of the crater: 41.60 south latitude, 202.30 east longitude.
Puzzle: could we design a helicopter that works on Mars? The gravity is weaker, but the atmosphere is thinner.
For more, see this:

WOW! Maria Leijerstam is now the first person to cycle to the South Pole! She arrived on December 27th.
She was racing against two men, and she arrived at the pole with a lead of hundreds of miles! It took her just 9 days to go 640 kilometers. She rode a custom-made recumbent tricycle whose great design let her cut through the gale-force winds and scale the Transantarctic Mountains — a route similar to Scott and Amundsen's famous South Pole expeditions. Her competitors had to go around, and that's a big part of why she won.
With the mountains behind her, Maria then faced a 480-kilometer journey over the polar plateau. Snow drifts, crevasses, whiteouts, rough grooved terrain and temperatures as low as -35° made it hard — but she cycled in 12-hour stints, and did up to 60 kilometers per day... for the win!
She's now back home in Wales. I love what people can do with the right technology together with intelligence and huge amounts of determination. She practiced for 4 years - watch this video:
For more see:

My mother sent me a box of old stuff including this photograph of my dad, Peter Baez... and the poncho he was wearing here! This would have been taken around 1958 or so.
© 2013 John Baez
baez@math.removethis.ucr.andthis.edu