I've already written about the first two hugely important tuning systems in Western music: Pythagorean tuning and just intonation. It's time to introduce the third: 'quarter-comma meantone’.
But first, remember the story so far!
Pythagorean tuning may go back to Mesopotamia, but it was widely discussed by Greek mathematicians — perhaps including Pythagoras, whose life is mainly the stuff of legends written down centuries later, but more certainly Eratosthenes, and definitely Ptolemy. It was widely used in western Europe in the middle ages, especially before 1300.
The principle behind Pythagorean tuning is to start with some pitch and go up and down from there by 'just fifths' — repeatedly multiplying and dividing the frequency by 3/2 — until you get two pitches that are almost 7 octaves apart. Here I'll do it starting with C:
But there are some problems. The highest tone is a bit less than 7 octaves above the lowest tone! Their frequency ratio is called the Pythagorean comma. And we get a total of 13 tones, not 12.
To deal with these problems, we can simply omit one of these two tones and use only the other in our scale. There are two ways to do this, which are mirror images of each other:
Each breaks the symmetry of the scale. And each gives one fifth that's noticeably smaller than the rest. It's called a 'wolf fifth' — because it's so out of tune it howls like a wolf!
What can we do? One solution is simply to avoid playing this fifth. You've probably heard the old joke. A patient tells his doctor: "It hurts when I lift my arm like this." The doctor replies: "So don't lift your arm like that!"
This worked pretty well for medieval music, where the fifth and octaves were the dominant forms of harmony, and people didn't change keys much, so they could avoid the wolf fifth. But in the late 1300s, major thirds became very important in English music, and soon they spread throughout Europe. A major third sounds perfectly in tune — or technically, 'just' — when it has a frequency ratio of
$$ \displaystyle{ \frac{5}{4} = 1.25 } $$
But the major thirds in Pythagorean tuning are bigger than this!
Let's see why. This will eventually lead us to the solution called 'quarter-comma meantone' tuning.
To go up a major third in Pythagorean tuning, we take any tone and go up 4 fifths, getting a tone whose frequency is
$$ \displaystyle{ \left(\frac{3}{2}\right)^4 = \frac{81}{16} } $$
times as high. Then we go down 2 octaves to get a tone whose frequency is
$$ \displaystyle{ \frac{81}{64} = 1.265625 } $$
times that of our original tone. This is called a Pythagorean major third. It's close to the just major third, 5/4 = 1.25. But it's a bit too high!
Let's see what what these Pythagorean major thirds look like, and where they sit in the scale. To do this, let's take our original 'star of fifths':
and reorder the notes so they form a 'circle of fifths':
Here we see two wolf fifths, each containing one of the notes separated by a Pythagorean comma (namely G♭ and F♯). As we've seen, if we omit either one of these notes we're left with a single wolf fifth. But this breaks the left-right symmetry of the above picture, so let's leave them both in for now.
Now let's draw all the Pythagorean thirds in blue:
A pretty, symmetrical picture. But not every note has a blue arrow pointing out of it! The reason is that not every note has some other note in the scale a Pythagorean third higher than it. We could delve into this more....
But instead, let's figure out what to do about these annoyingly large Pythagorean thirds!
Historically, the first really popular solution was to use 'just intonation', a system based on simple fractions built from the numbers 2, 3 (as in Pythagorean tuning) but also 5. It was discussed by Ptolemy as far back as 150 AD. But it became widely used from roughly 1300 to at least 1550 — starting in England, and then spreading throughout Europe, along with the use of major thirds.
Just intonation makes a few important thirds in the scale be just, but not as many as possible. Around 1523 another solution was invented, with more just thirds: 'quarter-comma meantone'. It became popular around 1550, and it dominated Europe until about 1690. Let's see what this system is, and why it didn't catch on sooner.
The idea is to tweak Pythagorean tuning so that all the Pythagorean thirds I just showed you become just thirds! To do this, we'll simply take the Pythagorean system:
and shrink all the blue arrows so they have a frequency ratio of 5/4.
Unfortunately this will force us to shrink the black arrows, too, In other words, to make our major thirds just, we need to shrink our fifths. It turns out that we need fifths with a frequency ratio of
$$ \displaystyle{ \sqrt[4]{5} \approx 1.49534878\dots} $$
This is only a tiny bit less than the ideal fifth, namely 1.5. It's not a nasty wolf fifth: it sounds pretty good. In fact it's quite wonderful that the fourth root of 5 is so close to 3/2. So, using some fifths like this may count as an acceptable sacrifice if we want just major thirds.
Here's what we get:
This tuning system is called quarter-comma meantone.
You'll note that by shrinking the blue and black arrows — that is, the thirds and fifths — we've now made the note F♯ lower than G♭, rather than higher, as it was in Pythagorean tuning. Their frequency ratio is now $$ \displaystyle{ \frac{128}{125} = 1.024} $$
which is yet another of those annoying little glitches: this one is called the lesser diesis.
So that's quarter-comma meantone tuning in a nutshell. But there's a lot more to say about it. For example, I haven't explained all the numbers in that last picture. Where do \(\sqrt[4]{5}\) and the lesser diesis 128/125 come from??? I haven't even explained why this system called 'quarter-comma meantone'. These issues are related. I'll explain them both next time, but I'll give you a hint now. I told you that the Pythagorean major third $$ \displaystyle{ \frac{81}{64} = 1.265625 } $$ is a bit bigger than the just major third: $$ \displaystyle{ \frac{5}{4} = 1.25 } $$
But how much bigger? Their ratio is $$ \displaystyle{ \frac{81/64}{5/4} = \frac{81}{80} = 1.0125 } $$$ This number, yet another of those annoying glitches in harmony theory, is called the syntonic comma. And this, not the Pythagorean comma, is the comma that gives 'quarter-comma meantone' its name! By taking the syntonic comma and dividing it into four equal parts — or more precisely, taking its fourth root — we are led to quarter-comma meantone. I'll show you the details next time.
Quarter-comma meantone is dramatically different from the earlier tuning systems I've discussed, since it uses an irrational number: the fourth root of 5. I think this is why it took so long for quarter-comma meantone to be discovered. After all, irrational numbers were anathema in the old Pythagorean tradition relating harmony to mathematics.
It seems that quarter-comma meantone was discovered in a burst of more sophisticated mathematical music theory in Renaissance Italy — along with other meantone systems, but I'll explain what that means later. References to tuning systems that could be meantone appeared as early as the 1496 text Practicae musica by Franchinus Gaffurius. Pietro Aron unmistakably discussed quarter-comma meantone in Toscanello in musica in 1523. However, the first mathematically precise descriptions appeared in the late 16th century treatises by the great Gioseffo Zarlino (Le istitutioni harmoniche, 1558) and Francisco de Salinas (De musica libri septem, 1577). Those two also talked about 'third-comma' and 'two-sevenths-comma' meantone systems.
December 18, 2023
Last time I introduced 'quarter-comma meantone', the tuning system shown above. Today let's see if we can understand all the numbers in this picture.
You see 13 circles with letters in them standing for tones in a scale, connected by arrows labeled by numbers. The numbers are the frequency ratios between these tones:
This is remarkably close to a 'just perfect fifth', with a frequency ratio of 3/2. We'd love to have a 12-tone scale with lots of just major thirds and just perfect fifths, but alas it's impossible!
Let's analyze what's going on with these three numbers by treating them as variables:
Here \(T\) stands for 'third' and it should be a number close to 5/4. \(F\) stands for 'fifth' and it should be close to 3/2. \(F\) should be close to 1.
If you look at the picture above you'll see one blue arrow takes you as far as four red arrows. You might naively think this implies \(T = F^4\) but that can't be true: for quarter-comma meantone we have \(F = \sqrt[4]{5}\) and \(T = 5/4\). So in fact
$$ \displaystyle{ T = \frac{F^4}{4} } $$
The point is that the notes in the picture represent not specific pitches but 'pitch classes': pitches modulo powers of 2. So, for example, you start at C and go up four fifths you get to E, but this E has frequency 4 times that of the E you get by going up a third from C.
Similarly, to go all the way around the circle you go along 12 red arrows and one purple arrow. You might naively think this means xF12 = 1. But in fact you've gone up 7 octaves: the frequency has gone up by a factor of 27. So in fact $$ x F^{12} = 2^7 $$ These are all the equations we need to get ourselves a scale: $$ F^4 = 4T, \qquad x F^{12} = 2^7 $$
We have 3 unknowns and just 2 equations, so we get a 1-parameter family of scales this way.
Delightfully, this family includes three of the most popular tuning systems in the last millennium of western music! They are the three most obvious choices: we can either take \(F = 3/2\), or \(T = 5/4\), or \(x = 1\)
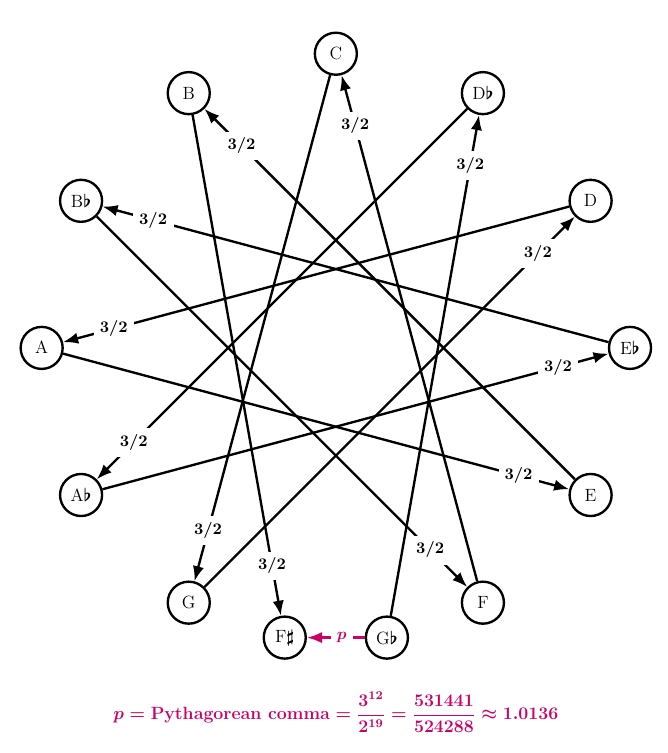
This gives Pythagorean tuning! In this system \(x\) is actually less than 1. Its reciprocal is called the Pythagorean comma. I may sometimes call this \(p\): $$ \displaystyle{ p = \textrm{Pythagorean comma} = \frac{3^{12}}{2^{19}} = \frac{531441}{524288} \approx 1.0136 } $$ Since \(x\) is less than 1, the diminished fifth (G♭) is actually below the augmented fourth (F♯). This makes something funny happen if we write the notes so that the frequencies keep going up as we go clockwise. Ponder this:
If we love major thirds and want these to be just, we must take \(T = 5/4\). Then our equations force $$ \displaystyle{ T = \frac{5}{4}, \qquad F = \sqrt[5]{4}, \qquad x = \frac{2^7}{5^3} } $$
This gives quarter-comma meantone! Now \(x\) is greater than 1, and it's called the lesser diesis. I'll sometimes call it \(\delta\): $$ \delta = \textrm{lesser diesis} = 2^7/5^3 = \frac{128}{125} = 1.024 $$
Here's what quarter-comma meantone looks like:
If we want our augmented fourth to be the same as the diminished fifth, we must take \(x = 1\). Then our equations force $$ \displaystyle{ T = \sqrt[3]{2}, \qquad F = 2^{7/12}, \qquad x = 1 } $$
This gives 12-tone equal temperament:
This scale has more symmetry than the other two, but all the frequency ratios are irrational except for octaves.
Pythagorean tuning ruled western music, or at least western music theory, from at least 1000 to 1300 AD. Quarter-comma meantone was dominant from about 1550 to 1690. Equal temperament ruled from about 1790 to now. It's remarkable that they come from three different points on this algebraic curve: $$ F^4 = 4T, \qquad x F^{12} = 2^7 $$ It would be interesting to study this curve a bit more using ideas from algebraic geometry.
You'll notice two gaps in that chronology! Just intonation flourished from about 1300 to 1550, and this system was based on a different idea: trying to get as many frequency ratios as possible to be simple fractions. I've discussed it in detail starting here. A rich and interesting variety of 'well-tempered' systems competed from about 1690 to 1790; these tweak the idea of quarter-comma meantone in various ways, and I'll talk about them later. Can we describe them using points on some higher-dimensional algebraic variety — a 'moduli space' of tuning systems? That's a question I want to keep in mind.
You'll notice some gaps in that chronology! Just intonation flourished from about 1300 to 1550, and this system was based on a different idea: trying to get as many frequency ratios as possible to be simple fractions. I've discussed it in detail starting here. A rich and interesting variety of 'well-tempered' systems competed from about 1690 to 1790; these tweak the idea of quarter-comma meantone in various ways, and I'll talk about them later.
I hope you understand the math underlying quarter-comma meantone a bit better now. But I still haven't said why it's called 'quarter-comma meantone'! For that we'll need to dig deeper into 'commas'. We'll need to understand those well to appreciate the well-tempered systems.
On December 13th I explained the tuning system shown above. But I didn't say why it's called 'quarter-comma meantone'.
Today I'll finally tell you what a 'quarter comma' is. Not only will this shed new light on this particular tuning system, it'll prepare you for understanding other meantone temperaments, like '1/3-comma', '1/6-comma' and so on.
As for the word 'meantone', that requires a whole other explanation. But one thing at a time!
We've already seen that there's a conflict built deep into the heart of music: a conflict between wanting lots of just perfect fifths, which are pairs of tones with frequency ratios of 3/2, and wanting lots of just major thirds, which are pairs of tones with frequency ratios of 5/4.
You can't have lots of both, though you can come close. The problem is that the fourth power of 3/2 is a bit more than 5: $$ \displaystyle{ \left( \frac{3}{2}\right)^4 = \frac{81}{16} = 5.0625 } $$
Their ratio is called the syntonic comma, and sometimes I'll call it \(\sigma\): $$ \sigma = \textrm{syntonic comma} = \frac{(3/2)^4}{5} = \frac{81}{80} = 1.0125 $$
As a result, going up 4 just perfect fifths is a bit more than going up a just major third and 2 octaves. The former increases the frequency by $$ \left( \frac{3}{2}\right)^4 = \frac{81}{16} = 5.0625 $$ while the latter increases it by $$ \frac{5}{4} \cdot 2^2 = \frac{80}{16} = 5 $$
The ratio of these is the syntonic comma.
In quarter-comma meantone, we make our perfect fifths a bit smaller to get our major thirds to be just. That is, we replace 3/2 by a slightly smaller number whose fourth power is exactly 5. Unsurprisingly, this number is none other than $$ \sqrt[4]{5} \approx 1.4953 $$ But here's another way to think about it: we take 3/2 and divide it by the fourth root of the syntonic comma! That way, when we raise the result to the fourth power, the syntonic comma cancels out the problem and we get exactly 5. So, I'm saying $$ \sqrt[4]{5} = \frac{3}{2} \sigma^{-1/4} $$
If this isn't obvious from what I've already said, do the math — it'll be good for you.
Musicians will say we've lowered our fifth by a quarter comma, since they implicitly take logarithms: when I say we're dividing by the fourth root of the syntonic comma, they say we're subtracting a quarter of a comma. I won't be talking that way, but I can still draw a picture of the quarter-comma meantone tuning system that shows these 'quarter commas':
Notice that we've got 12 of these quarter commas, one between every pair of notes except the devilish F♯ and G♭. That's a total of 3 commas. We can imagine systems where these 3 commas are distributed in other ways, and we'll be seeing a bunch of them soon, when we get to well-tempered tuning systems. What quarter-comma meantone does is spread out these commas as evenly as possible.
But what about those notes F♯ and G♭? As I've said before, we usually leave out one of those, to get a scale with 12 more or less equally spaced notes. Next time I'll show you what happens then.
It's hard to see it, but this guy is playing Scottish folk music in my favorite pub in Edinburgh, on Christmas eve... on a bouzouki! This instrument jumped from Greece to Ireland in the 60s, but now it's used in Scottish folk music too.
For more on the Irish bouzouki, try this:
I've been talking about the marvelous tuning system that dominated western music from about 1550 to 1690: quarter-comma meantone. Above I've drawn it in its most mathematically beautiful form. For convenience I'm drawing it in the key of C, but you could use any key.
This scale has lots of 'just major thirds', which are pairs of notes with a frequency ratio of 5/4. I've drawn them as dark blue arrows.
This scale also has a visible symmetry under reflection across the vertical axis! What does this mean musically? It means that if you can reach some note in the scale by starting at C and multiplying the frequency by some number, you can reach some other note in the scale by starting at C and dividing by that number. Musicians call this symmetry 'inversion'.
Unfortunately this scale has 13 notes, not 12. But the real problem is not that 13 is an unlucky number. It's that two of the notes are absurdly close together! Their frequency ratio is a number very close to 1, called the 'lesser diesis': $$ \displaystyle{ \delta = \textrm{lesser diesis} = \frac{2^7}{5^3} = \frac{128}{125} = 1.024 } $$
So in practice, musicians usually leave out one of these two notes. This breaks the symmetry but gives a scale with 12 notes that are close to equally spaced.
Usually musicians leave out the higher of these two nearby notes, called the diminished fifth. When we're in the key of C, as above, this is the one called G♭. With G♭ removed, we're left with the following scale:
Now there's one fewer of those dark blue arrows: one just major third is gone. Also, our scale now has a 'wolf fifth' with frequency ratio audibly bigger than 1.5. So, we pay a price for breaking the symmetry and leaving out the diminished fifth.
Alternatively, we could leave out the lower of the two nearby notes, called the augmented fourth. This is the one called F♯. Then we get this scale:
It's just a reflected version of the scale above.
Is there any good reason to prefer the choice most people make, namely leaving out the diminished fifth? As a mathematician you might say "no, the two choices are related by a symmetry, so the choice we make is completely arbitrary". However, the symmetry we're talking about here — inversion symmetry, where we replace frequency ratios by their reciprocals — is not some god-given law of nature. After all, when you pluck a guitar string you hear an 'overtone series': not just the fundamental frequency but also the frequencies 2, 3, 4, etc. times that. You don't hear an 'undertone series' with frequencies 1/2, 1/3, 1/4 etc. times the fundamental!
People do try to do music with undertones, and it's fun — it's called 'negative harmony'. But undertones are physically not on an equal footing with overtones. And while a major triad and a minor triad are related by inversion symmetry, they sound very different. So there could be a reason to prefer the scale with an augmented fourth to the one with the diminished fifth. But I don't know it.
As I keep emphasizing, trying to create a nice tuning system is like trying to make your carpet look good when it's too big for your room. There are bound to be lumps in the carpet; all you can do is try to deal with them as best you can. You can try to spread them out evenly, try to gather them into one big lump and hide it under the couch, etc.
So, the math of tuning systems is the math of lumps. We can learn more about this by comparing quarter-comma meantone with Pythagorean tuning. Le's compare the versions that are missing the diminished fifth. We'll find a nice relation between three pesky numbers that are quite close to 1:
First let's take our quarter-comma meantone scale:
and write it using letter names for the lesser diesis and syntonic comma. I'll leave out the blue arrows, because we won't need them:
As we go all the way around this circle clockwise, the frequency goes up by 7 octaves. So, multiplying all the numbers labeling the arrows, we must have $$ \displaystyle{ \left( \frac{3}{2} \sigma^{-1/4} \right)^{12} \delta = 2^7 }. $$
As you can see, here the lumps in the carpet are the cube of the reciprocal of the syntonic comma, which we have smeared out over the whole circle of fifths, together with the lesser diesis, which we've concentrated in the wolf fifth.
On the other hand Pythagorean tuning is based on fact that going around this circle, we go up 7 octaves:
Mathematically this says $$ \displaystyle{ \left(\frac{3}{2}\right)^{12} p^{-1} = 2^7 }. $$
where \(p\) is the Pythagorean comma. So here the lump in the carpet is the reciprocal of the Pythagorean comma, which we've packed into the wolf fifth.
Putting these two equations together we see
$$ \displaystyle{ \sigma^{-3} \delta = p^{-1} } $$
or in other words $$ \displaystyle{ p \delta = \sigma^3}. $$
The Pythagorean comma times the lesser diesis is the syntonic comma cubed! Knowing this may help us later, when I discuss the fancier methods of dealing with lumps in the carpet used in well-tempered scales.
First, however, I want to explain that word 'meantone'. What's mean about the tones in quarter-comma meantone? I'll tell you next time!
I've been talking about the quarter-comma meantone tuning system, which dominated western music from about 1550 to 1690. So far I've been drawing it using a circle of fifths, as above. This is a diagram where as we go clockwise each note is a fifth higher than the previous one.
But why is this system called 'meantone'? Briefly, it's because the size of a whole step between notes in this tuning system — called a 'tone' — is the geometric mean of the two kinds of whole step in Pythagorean tuning!
Let's figure this out. First we need to understand the frequency ratio of two neighboring notes separated by a half step, called a 'semitone'.
We can figure it out using pictures. Let's start by getting rid of the blue arrows for major thirds, which just clutter things up now:
Next, let's take this diagram and reorder the notes so they go up the chromatic scale: C, C♯, D, E♭, E, etc. This turns our circle of fifths into a 'star of fifths':
Now let's figure out the frequency ratios of neighboring notes! First, lets go up from C to C♯.
Follow the path from C to C♯ in the picture above. As you do, you'll go up 7 quarter-comma fifths, but you'll also hit the lesser diesis. Multiplying all these numbers you get $$ \displaystyle{ \frac{128}{125} \cdot 5^{7/4} = \frac{128}{5^{5/4}} \approx 17.12 }. $$ This is a lot bigger than 1, so you've gone up to some C♯ that lies octaves above our original C. You should divide by an appropriate power of 2 to get the C♯ right next to our original C. Namely, you should divide by 16. This gives $$ \displaystyle{ \frac{8}{5^{5/4}} \approx 1.06998}. $$
So this is how much you multiply the frequency of C to get the C♯ right above it! This number is called the quarter-comma diatonic semitone.
Next, let's go up from C♯ to D.
With your finger or eye, follow the path from C♯ to D:
So this is how much we multiply the frequency of C♯ to get the D right next to it. This number is called the quarter-comma chromatic semitone.
If you go through all the notes of the scale you'll see they're all spaced by diatonic or chromatic semitones... with one exception, namely the tiny space between F♯ and G♭, which is just the lesser diesis.
Indeed, we get this pattern of semitones:
To see it better, we can remove the scaffolding of fifths:
By the way, since the diatonic semitone includes the lesser diesis while the chromatic semitone does not, we get this relation:
Okay, but what does all this have to do with the term 'meantone'? Well, in music a 'tone' is two semitones. Since the semitones in quarter-comma meantone generally alternate between diatonic and chromatic, a tone is usually equal to
Fans of the golden ratio will notice that this number is 1/2 less than that!
But the name 'meantone' arises because this number \(\sqrt{5}/2\) is the geometric mean of the two kinds of tones in just intonation, namely 9/8 and 10/9: $$ \sqrt{\frac{9}{8} \cdot \frac{10}{9}} = \frac{\sqrt{5}}{2}. $$
While the tones in just intonation hop back and forth between the larger 9/8 and the smaller 10/9, in quarter-comma meantone they generally stay at the mean of those two... which you might even call the golden mean!
It's sort of ridiculous that I've never studied even the very basics of Indian music, like what are the ragas. Thanks to my friend Todd Trimble I'm dipping my toe into it. And it turns out that in Carnatic music, one of the two main kinds of Indian classical music, the 72 Melakarta ragas are just subsets of the usual 12-tone scale!
I just learned why there are 72. Let's use western notation and call the 12-tone scale
To be a Melakarta raga, a subset of these tones needs to obey some rules:
This gives a total of 2 × 6 × 6 = 72 options!
All this seems very reasonable by western standards: it's just very systematic and thus includes more cases than the most common western modes. Really good jazz musicians probably think about all these scales.
For example, Mayamalavagowla is one of the spicier ragas recommended for beginners on VoxGuru:
It's spicy because it has a minor second:
In western terminology it's called the 'double harmonic’ or 'Byzantine' scale, and it was famously used in Dick Dale's surf rock classic Misirlou:
But beware! There are many more ragas, called 'janya ragas', derived from the basic 72 by leaving out notes and other tricks. This calculation claims there are 28,864 possible janya ragas:
There is more information here, but I haven't been able to access this paper:
In the previous entry I said a little about ragas in Carnatic music, which is prevalent in the south of India. Now let me give an equally superficial introduction to ragas in Hindustani music, which is prevalent in the north.
In Carnatic music we start with 72 different seven-note scales called 'Melakarta ragas', and then build many more ragas by leaving out notes and other tricks. Hindustani music is a bit similar: we start with 32 seven-note scales called 'thaats', and then build many ragas by leaving out notes and other tricks.
I should admit right away that this is not how ragas arose historically: both Carnatic and Hindustani music have been going on for centuries, and they diverged in the 1100s. But the Melakarta ragas were used to organize Carnatic music only around 1640, and the thaats were introduced to do the same for Hindustani music even later, in the early 20th century. Furthermore, everything in reality is more messy than the mathematician would like it to be. For example, there are Hindustani ragas that don't fit into the thaat system.
But let's just do the math of thaats, and see why there are 32 of them. I'll use western notation and call the 12-tone scale
To be a thaat, a subset of these tones needs to obey some rules:
As you can see, it shows 5 binary choices leading to a total of 32 thaats. But what do the letters mean?
The notes in any thaat are called
or for short
These are a lot like the western "do re mi fa so la ti". But for only 5 of these notes, namely R G M D N, do we have a choice: we can use them unmodified, as in the major scale, or we can alter them. That's what the chart shows.
Now it's time to admit a bit more reality into the discussion. Of the 32 theoretically possible thaats, Bhatkhande chose to focus on ten. These are more popular than the rest! Let's see what they're like.
(There exists a seventh mode of the major scale, Locrian. But it can't be a thaat, because it has a flat 5.)
In my previous diary entry I showed you a rare western pop song in the double harmonic scale.
But that name is ridiculously long, so it might be better to call it Phrygian ♯4 ♮7.
Different ragas are meant to be played at different times of day, and Poorvi is performed at sunset. Here's an example:
If you want vocal pyrotechnics, start around 29 minutes in. There you will hear that passages often end by dropping down a half-step from the minor second to the tonic (i.e. D♭ to C if we were in the key of C). By western standards this is a very unusual cadence. But that's why I like it! This piece doesn't shy away from the minor 2nd — it really leans into it.
December 29, 2023
Traditional western music theory embraces chords with frequency ratios that are products of powers of 2, 3, and 5... but not higher primes. Barbershop quartets go further!
These quartets love four-part harmony using dominant seventh chords. A dominant seventh chord contains a note, its major third, its perfect fifth, and its minor seventh. In traditional harmony these have frequencies proportional to 4, 5, 6, and ... not 7, because that would be against the rules, but instead some number close to it. Barbershop quartets break the rules and use 7.
Gage Averill writes:
Society arrangers believe that a song should contain anywhere from 35 to 60 percent dominant seventh chords to sound 'barbershop' — and when they do, barbershoppers speak of being in 'seventh heaven.'Art Merill writes:
There's a chord in a barbershop that makes the nerve ends tingle....We might call our chord a Super-Seventh! ... The notes of our chord have the exact frequency ratios 4–5–6–7. With these ratios, overtones reinforce overtones. There's a minimum of dissonance and a distinctive ringing sound. How can you detect this chord? It's easy. You can't mistake it, for the signs are clear; the overtones will ring in your ears; you'll experience a spinal shiver; bumps will stand out on your arms; you'll rise a trifle in your seat.The frequency ratio
is called the harmonic seventh. In Pythagorean tuning, where we only get to use the primes 2 and 3, the closest simple approximation is the Pythagorean minor seventh:
which is sharp by a factor of
This number is called the septimal diesis.
Of course we can also use the Pythagorean minor seventh in 5-limit tuning (often called just intonation), where we get to use the primes 2, 3 and 5. Then it's called the small just minor seventh. But in 5-limit tuning we also have a better simple approximation to 7/4 = 1.75, called the large just minor seventh:
This is sharp by a factor of
This number is called the septimal comma or Archytas' comma.
By the way, it's essentially just a coincidence that the minor seventh sounds good with a frequency ratio involving the number 7. It's called a minor seventh because it's the seventh note in the minor scale! In just intonation, the interval called a major third involves the number 5 (it's 5/4), while the interval called a perfect fifth involves the number 3 (it's 3/2). So, be careful!
For much more about 7-limit tuning, which only uses the primes 2, 3, 5, and 7, read this:
For a bit less, try this:
December 30, 2023
Sometimes we wake up, open the shutters, and the view of Arthur's Seat
is beautiful despite the condensation on the windows.
