

I saw this in a post by the mathematician Richard Green, who explains the underlying math quit nicely. But it's been making the rounds for a while.
There are different kinds of Morse code: this is International Morse Code.
Each letter or number is represented by a sequence of dots and dashes. When you type these out on a telegraph, a dash should be 3 times as long as a dot. Each dot or dash is followed by a short silence, as long as a dot. The letters of a word should be separated by a silence that's 3 dots long, and words should be separated by a silence that's 7 dots long.
How long is a dot? That depends on your skills!
The codes for numbers make a pattern. The codes for letters look chaotic. But they're not: they're chosen so that commonly used letters have short codes! The system is nicely explained using a tree:
E and T are on top: they have the shortest codes, because they are very commonly used letters. The E is a single dot and the T is a single dash. Then come I, A, M and N. And so on.
How good is International Morse Code? For that you should compare the tree it uses to the tree it would use if it were as good as possible. The best possible way is called a Huffman coding. You can see it on page 16 here:
"So you traveled the whole twenty light years?"These are two quotes from this story:"More than that," Joan said truthfully, "from my original home. I've spent half my life traveling".
"Faster than light?" Pirit suggested hopefully.
"No. That's impossible".
They circled around the question a dozen more times, before Pirit finally changed her tune from how to why?
"I'm a xenomathematician," Joan said. "I've come here in the hope of collaborating with your archaeologists in their study of Niah artifacts."
Pirit was stunned. "What do you know about the Niah?"
"Not as much as I'd like to." Joan gestured at her Noudah body. "As I'm sure you've already surmised, we've listened to your broadcasts for some time, so we know pretty much what an ordinary Noudah knows. That includes the basic facts about the Niah. Historically they've been referred to as your ancestors, though the latest studies suggest that you and they really just have an earlier common ancestor. They died out about a million years ago, but there's evidence that they might have had a sophisticated culture for as long as three million years. There's no indication that they ever developed space flight. Basically, once they achieved material comfort, they seem to have devoted themselves to various artforms, including mathematics."
"So you've traveled twenty light years just to look at Niah tablets?" Pirit was incredulous.
"Any culture that spent three million years doing mathematics must have something to teach us."
"Really?" Pirit's face became blue with disgust. "In the ten thousand years since we discovered the wheel, we've already reached halfway to the Cataract. They wasted their time on useless abstractions."
Joan said, "I come from a culture of spacefarers myself, so I respect your achievements. But I don't think anyone really knows what the Niah achieved. I'd like to find out, with the help of your people."
[...]
"Jown! Jown! Come and look at this!" Surat called to her. Joan switched off the tomography unit and jogged toward the archaeologists, suddenly conscious of her body's strangeness. Her legs were stumpy but strong, and her balance as she ran came not from arms and shoulders but from the swish of her muscular tail.
"It's a significant mathematical result," Rali informed her proudly when she reached them. He'd pressure-washed the sandstone away from the near-indestructible ceramic of the tablet, and it was only a matter of holding the surface at the right angle to the light to see the etched writing stand out as crisply and starkly as it would have a million years before.
Rali was not a mathematician, and he was not offering his own opinion on the theorem the tablet stated; the Niah themselves had a clear set of typographical conventions which they used to distinguish between everything from minor lemmas to the most celebrated theorems. The size and decorations of the symbols labelling the theorem attested to its value in the Niah's eyes.
Joan read the theorem carefully. The proof was not included on the same tablet, but the Niah had a way of expressing their results that made you believe them as soon as you read them; in this case the definitions of the terms needed to state the theorem were so beautifully chosen that the result seemed almost inevitable.
The theorem itself was expressed as a commuting hypercube, one of the Niah's favorite forms. You could think of a square with four different sets of mathematical objects associated with each of its corners, and a way of mapping one set into another associated with each edge of the square. If the maps commuted, then going across the top of the square, then down, had exactly the same effect as going down the left edge of the square, then across: either way, you mapped each element from the top-left set into the same element of the bottom-right set. A similar kind of result might hold for sets and maps that could naturally be placed at the corners and edges of a cube, or a hypercube of any dimension. It was also possible for the square faces in these structures to stand for relationships that held between the maps between sets, and for cubes to describe relationships between those relationships, and so on.
That a theorem took this form didn't guarantee its importance; it was easy to cook up trivial examples of sets and maps that commuted. The Niah didn't carve trivia into their timeless ceramic, though, and this theorem was no exception. The seven dimensional commuting hypercube established a dazzlingly elegant correspondence between seven distinct, major branches of Niah mathematics, intertwining their most important concepts into a unified whole. It was a result Joan had never seen before: no mathematician anywhere in the Amalgam, or in any ancestral culture she had studied, had reached the same insight.
She explained as much of this as she could to the three archaeologists; they couldn't take in all the details, but their faces became orange with fascination when she sketched what she thought the result would have meant to the Niah themselves.
"This isn't quite the Big Crunch," she joked, "but it must have made them think they were getting closer". The Big Crunch was her nickname for the mythical result that the Niah had aspired to reach: a unification of every field of mathematics that they considered significant. To find such a thing would not have meant the end of mathematics — it would not have subsumed every last conceivable, interesting mathematical truth — but it would certainly have marked a point of closure for the Niah's own style of investigation.
Read the whole thing! The start is quite dramatic!
The image above is not alien mathematics; it's from an article about a codes for communicating with extraterrestrial civilizations:
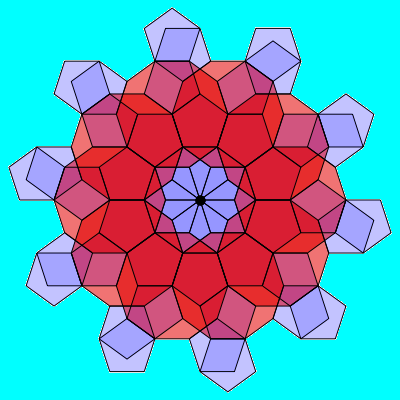
Greg Egan and I have been exploring the 'forbidden tilings'. These are ways to stick together shapes that look like they should tile the plane, but don't.
Two regular pentagons and a regular decagon fit snugly at a point: their interior angles sum to 360°. Despite this, you cannot tile the plane with regular pentagons and decagons!
But you can do some other things. The above picture by Egan shows one of them.
The idea here is to start drawing regular pentagons and decagons on the plane, and make sure that:
The pentagons and decagons will overlap, and the picture will get very confusing, so here Egan shows just one stage of drawing the picture. To see more stages, visit my American Mathematical Society blog:
What's really going on here? It's secretly all about non-Euclidean geometry! There's a way to tile the hyperbolic plane by regular pentagons and decagons. It's very symmetrical, and the shapes don't overlap.
Then, there's a way to map the hyperbolic plane down to the ordinary Euclidean plane. This has infinitely many 'branch points'. If you walk around a branch point in the hyperbolic plane, your shadow down in the Euclidean plane will walk three times around a point down there.
This is how we get 10 pentagons to meet at a point. Up in the hyperbolic plane, they don't overlap. Down in the Euclidean plane, they do: they wrap three times around a point. That's what you see in the very middle of this picture!
You can learn more of the underlying math at the link above. For a cool-looking failed attempt to tile the Euclidean plane with regular pentagons and decagons, try this:

How can computers get legal rights like people? It sounds hard. But in the US, it's not. They just need to become corporations.
You see, in the US, corporations are already persons in the legal sense, with the right to sign contracts and sue people. In 2010, the Supreme Court said they have the right to free speech! Since corporations are very powerful, they are likely to gain more and more rights — and not just in the US.
So, computers might take over the world by becoming corporations... or running corporations.
Most people think computers need to be intelligent before they take over the world. But maybe it will go like this. First they become corporations. Then they hire us to make them more intelligent.
Now there's a company that's trying to speed up this process! It's called Ethereum. They want to help developers start Distributed Autonomous Corporations: corporations run by computers.
Vitalik Buterin, who runs Ethereum, explained the basic idea:
Corporations, US presidential candidate Mitt Romney reminds us, are people. Whether or not you agree with the conclusions that his partisans draw from that claim, the statement certainly carries a large amount of truth. What is a corporation, after all, but a certain group of people working together under a set of specific rules? When a corporation owns property, what that really means is that there is a legal contract stating that the property can only be used for certain purposes under the control of those people who are currently its board of directors — a designation itself modifiable by a particular set of shareholder. If a corporation does something, it's because its board of directors has agreed that it should be done. If a corporation hires employees, it means that the employees are agreeing to provide services to the corporation.s customers under a particular set of rules, particularly involving payment. When a corporation has limited liability, it means that specific people have been granted extra privileges to act with reduced fear of legal prosecution by the government — a group of people with more rights than ordinary people acting alone, but ultimately people nonetheless. In any case, it's nothing more than people and contracts all the way down.He went on to explain a plan to do this:However, here a very interesting question arises: do we really need the people? On the one hand, the answer is yes: although in some post-Singularity future machines will be able to survive all on their own, for the foreseeable future some kind of human action will simply be necessary to interact with the physical world. On the other hand, however, over the past two hundred years the answer has been increasingly no. The industrial revolution allowed us, for the first time, to start replacing human labor with machines on a large scale, and now we have advanced digitized factories and robotic arms that produce complex goods like automobiles all on their own. But this is only automating the bottom; removing the need for rank and file manual laborers, and replacing them with a smaller number of professionals to maintain the robots, while the management of the company remains untouched. The question is, can we approach the problem from the other direction: even if we still need human beings to perform certain specialized tasks, can we remove the management from the equation instead?
Most companies have some kind of mission statement; often it's about making money for shareholders; at other times, it includes some moral imperative to do with the particular product that they are creating, and other goals like helping communities sometimes enter the mix, at least in theory. Right now, that mission statement exists only insofar as the board of directors, and ultimately the shareholders, interpret it. But what if, with the power of modern information technology, we can encode the mission statement into code; that is, create an inviolable contract that generates revenue, pays people to perform some function, and finds hardware for itself to run on, all without any need for top-down human direction?
Does this make you want to rebel? It may be too late. I, for one, welcome our new robot overlords.
I thank Daniel Estrada for pointing out this article on DACs:

A cloud of ideas coalesces to form a brilliant insight. At first it seems big and important. Then you start taking it for granted... and it becomes one of the ingredients of your next insight.
I got this from Maria Dubai.