For my December 2017 diary, go here.

Diary — January 2018

John Baez

Last year was a bad year for me. Not just because the US has fallen into the hands of a buffoonish, lying, incompetent, self-absorbed would-be dictator. Not just because our puppet Congress voted to hand 1.5 trillion dollars to their wealthy masters. Not just because the world is teetering on the brink of a nuclear war with North Korea. Not just because the Tories have trapped themselves into ripping the UK out of the EU. Not just because climate change is breeding disasters — Harvey flooding Texas, Irma destroying Puerto Rico, half that island still without electric power, California burning, etc. — while the incompetent buffoon tries to prop up the dying coal industry and his henchmen erase the words "climate change" from government websites. All this is our common woe.

Last year my mother died on March 15th. In the photo above, taken before I was born, she looks rather feline and glamorous. My own memories of her are quite different, but she was always her own person — unconventional, indomitable.

The daughter of farmers in Grand Rapids, Michigan, she went to college and studied art. Then she taught it at a local high school — just long enough to save up money for a trip around the world. A friend of hers who planned to travel with her got pregnant and bailed out at the last minute. So she went alone, taking a steamer to Japan. She fell in love with their esthetics, and it stuck with her the rest of her life. Then she went to Angkor Wat, India, and so on. She had pizza for the first time in Italy: this was another age.

When she returned, Michigan was not exciting enough for her, so she moved to San Francisco. She taught art and hung out with Zen monks. My dad met her at party there, on the fringe of the beatnik scene of the late 1950s. He brought over some jazz records, conveniently forgot them, came back the next day to pick them up... and in a year they were married.

When I was in high school, she had us buy 5 acres in the woods and build a house there in the style of Frank Lloyd Wright. Later she decorated it with art, ceramics and textiles. Later she spent her time making jewelry. She was always focused on visual esthetics, with an intense perfectionism.

My knowledge of math and physics goes back to my dad and uncle, but my knowledge of music, art and religion is mainly due to her. Sure, my dad liked jazz and taught me how to play the recorder — but she liked Miles Davis, the Modern Jazz Quartet, Bartok and Ravi Shankar. I read my dad's books on logical positivism — but also her books on Zen and Taoism.

More importantly, she taught me to always seek out what was really interesting. It's a waste of time to pay attention to mediocre crap just because other people do. This has always seemed obvious to me. But I'm slowly realizing why. I was very lucky to have parents who lived that way.

I'm not very good at dealing with negative emotions: I tend to suppress them, let them fester. I heard the news of my mother's death while I was meeting my grad students, teaching them category theory — a phone call from my sister. I froze inside and soldiered on. As I spent this year dealing with my mother's estate, I found myself becoming not sad but angry. Every day, waking up to see the evil clown president dragging our country down, too busy reading contracts and talking to lawyers to think about math.... a world of pointless bullshit. I need to apologize to my wife and everyone else who suffered through my bitter moods.

Things are getting a bit better now — if not in the world at large, at least in my tiny corner. The legal work on my mom's estate is winding down. Her house is sold. I'm getting back the joy in life that powers me forward.

My mother died at 87, probably very happy that she didn't have to move out of her house into an old age home, as she'd been planning, very reluctantly, to do. She lived a great life, and she always said that dying would be okay. No condolences required.

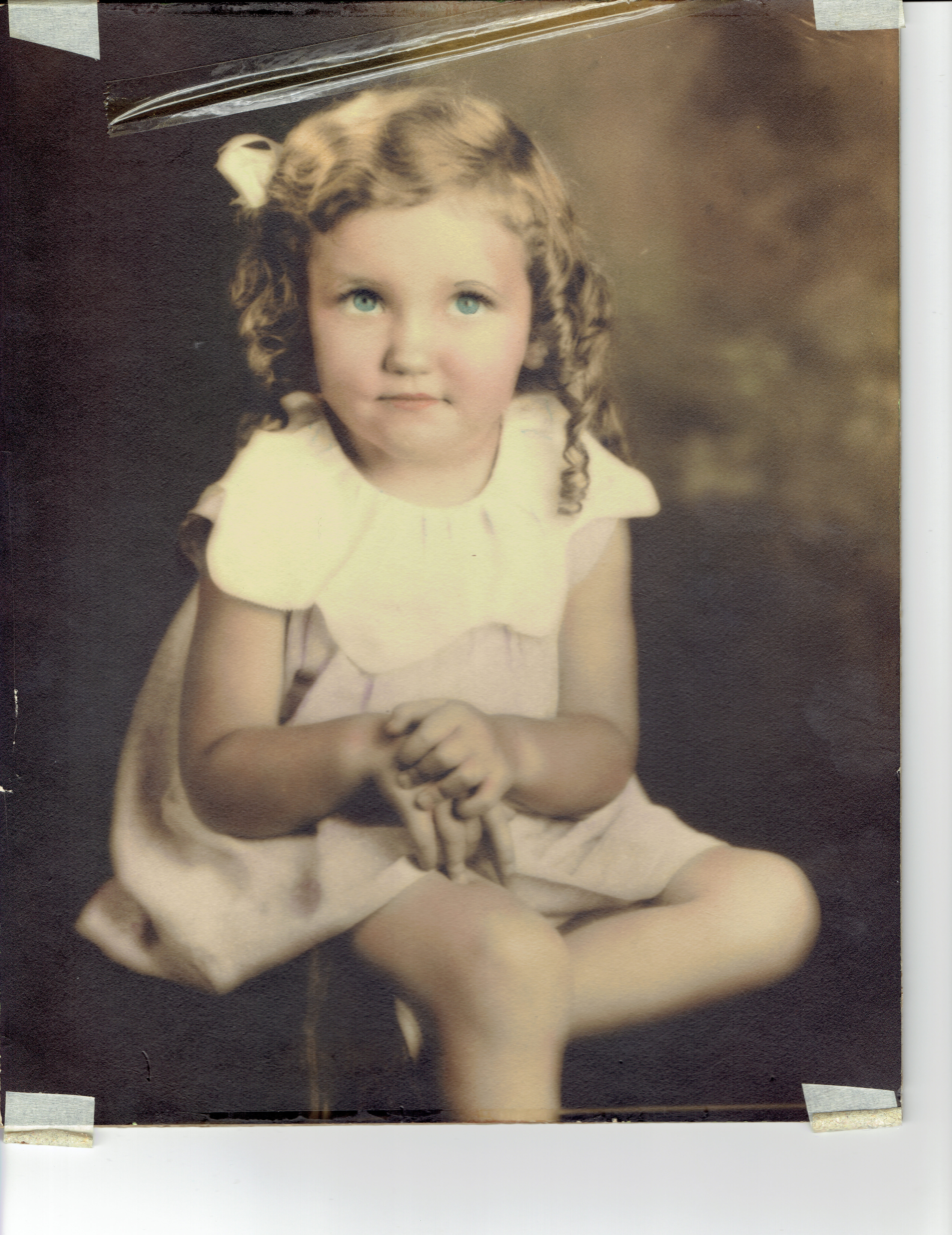
New Year's Resolution: do all my procrastination right now — don't keep putting it off.

I figure if I completely waste the first day of the year, I'll be ready to work ceaselessly starting tomorrow.

So, after lying in bed browsing the web for a few hours and listening to the radio, I got up and had pancakes for breakfast. Then I read old magazines that had been accumulating by my bed. Then I spent a few hours taking photos and putting them in my online diary.

The one above, created by Greg Egan, shows a shape morphing between a cuboctahedron and a regular icosahedron. When we bisect the edges of a regular tetrahedron, we get 12 points that form the vertices of a cuboctahedron. But when we divide these edges in the proportion of the golden ratio, we get 12 points that form the corners of a regular icosahedron!

It's fun to watch this, so I spent half an hour doing that. Note that as the icosahedron becomes a cuboctahedron, some pairs of the 20 triangular faces flatten out to form squares.

I've almost run out of ways to procrastinate — I guess I'm not very good at this. Pretty soon I'll have to start working! I have a bunch of papers to finish off.

Hey, I know — I can waste some more time by listing them! I've heard that listing your goals is a good way to postpone actually achieving them.

• Network models, with John Foley, Joseph Moeller and Blake Pollard. This is about using categories and operads to design systems of mobile, interacting agents. John works for Metron Scientific Solutions, and they're helping the Coast Guard create a tool to design search and rescue missions. But I'm over at the theoretical end of this project. Our paper is done, and we just need to take a few last looks at it, make sure it's okay, and submit it for publication.

• Struggles with the continuum. This is about ways in which assuming space is a continuum causes trouble in our favorite theories of physics — infinities and stuff like that. I need to edit the introduction, because it talks a lot about the foundations of mathematics, while the paper itself is all about physics. It somehow fools the reader into thinking the paper is going in a different direction than it actually does. I've been putting this off, because I'm not quite sure how to handle it.

• Coarse-graining open Markov processes with Kenny Courser. This studies a double category where the horizontal arrows are open Markov processes and the squares are 'coarse-grainings': ways of simplifying an open Markov process. The paper is almost done, we just need to insert some extra figures and make sure the notation is optimal.

• Magnitude homology versus persistent homology with Nina Otter. Persistent homology is really fashionable in 'topological data analysis', where you do things like try to count the number of holes in a cloud of data. Magnitude homology, on the other hand, was created by category theorists because of its beautiful abstract properties. They should be related and they are. We explain how they are. But we need to finish writing this paper!

So those are the main things I'm not doing yet. Starting tomorrow I'll get to work.

January 4, 2018

Many asteroids belong to families. These formed when bigger asteroids collided and broke into pieces. Asteroids in a family have similar orbits. But finding these families takes work!

This picture makes it look easy. But it's hard. In reality, the different families don't come in different colors. There are lots of asteroids that don't belong to families, not shown on this chart. And there's another even more important reason!

We can describe an orbit using some numbers. An orbit is an ellipse. The semimajor axis is half the length of this ellipse. The eccentricity says how stretched-out the ellipse is: it's 0 for a circle. The inclination is an angle that describes the orbit's tilt. Most planets have inclination almost zero, because they move close to a plane called the ecliptic.

So, you might try to find asteroid families by taking lots of asteroids and making a chart of their semimajor axis, eccentricity and inclination. Would that work? This picture makes it seem so!

But it wouldn't work. You'd get random junk — no obvious families.

To find the families, you have to correct for the fact that orbits keep changing! Look at this picture:

How does this 'correction' business work? It was invented by the Japanese astronomer Kiyotsugu Hirayama in 1918. He noticed that asteroid orbits change in a roughly periodic way over thousands of years due to the gravitational pull of the planets... but one can create ideal unchanging orbits by correcting for this fact.

Hirayama didn't have a computer, so he had to do these computations by hand, approximately! He succeeded in finding several families of asteroids this way: the Koronis, Eos, and Themis families, and later the Flora and Maria families.

By now we can do much better, and find many more families... and more asteroids in each family. For example, the Eos family was formed about 1.1 billion years ago between Jupiter and Mars. Hirayama found 19 asteroids in this family. The biggest, which gives the family its name, is Eos, named after the Greek goddess of the dawn. It's almost 100 kilometers across! But now we know almost 300 members of this family.

Here's what Wikipedia says about this business of correcting orbits:

The proper orbital elements of an orbit are constants of motion of an object in space that remain practically unchanged over an astronomically long timescale. The term is usually used to describe the three quantities:_

• proper semimajor axis (\(a_p\)),
• proper eccentricity (\(e_p\)), and
• proper inclination (\(i_p\)).

The proper elements can be contrasted with the osculating Keplerian orbital elements observed at a particular time or epoch, such as the semi-major axis, eccentricity, and inclination. Those osculating elements change in a quasi-periodic and (in principle) predictable manner due to such effects as perturbations from planets or other bodies, and precession (e.g. perihelion precession). In the Solar System, such changes usually occur on timescales of thousands of years, while proper elements are meant to be practically constant over at least tens of millions of years.

I suspect the math here is quite interesting. Unfortunately Wikipedia doesn't go into details.

For a table of asteroid families, go here:

• Wikipedia, Asteroid family.

The picture at the top of this entry is from here:

• Joel Duff, Rewinding the clock: an asteroid family history, Naturalis Historia, May 14, 2014.

In the discussion on my G+ post, Greg Roelofs took a look at this picture and wondered what distinguished the Eunomia family from the Adeona family: they overlap in this chart. It turns out the Eunomia family consists of bright S-type asteroids, which are 'stony': mainly made of iron and magnesium silicates. The Adeona family consists of dark C-type asteroids, which are 'carbonaceous'.

He also asked about the overlapping Hygeia family and Themis family. It turns out these can be distinguished by their inclination, but not so much by their semimajor axis and eccentricity.

January 11, 2018

Al Grant has a great interactive page of tilings that move on 'hinges'. Check it out:

• Al Grant, Hinged tesselations (part 1), February 1, 2014.

This is a flying fox. What could be cooler than flying foxes?

How about this: megabats.

'Megabats' sound like science-fictional monsters with 12-foot wing spans, swooping down in ruthless packs. But no, it's a standard scientific term. Bats come in two main kinds: the insect-eating microbats and the fruit-eating megabats, which include flying foxes.

At least that was the story until recently.

The fruit-eaters are generally larger than the insectivores, so the order of bats, Chiroptera, was subdivided into the Macrochiroptera or megabats and Microchiroptera or microbats. But this subdivision was recently found to be somewhat incorrect, so now the two suborders or bats are called — get ready for this! — Yinpterochiroptera and Yangopterochiroptera.

That's right: yin and yang, the Taoist terms for cold and hot, or dark and light, or negative and positive!

Puzzle. Who started using these terms for bats, and why?

In China, bats are considered lucky. At several Taoist monasteries I've visited, I've seen carvings of bats on the walls. But that could be a red herring.

Anyway, I'll use the old names for now. Here's how to tell the difference between megabats and microbats:

1. In general megabats are larger and eat fruit, while microbats are smaller and eat insects. However, there are exceptions. For example, vampire bats, which drink blood, are descended from fruit-eating bats that developed sharp teeth that could puncture thick-skinned fruit... but these particular fruit-eating bats are microbats!
2. Microbats use echolocation, whereas megabats generally don't. It seems they have lost this trait because they're looking for plants rather than insects, and they use more energy flying than the microbats. Again there's an exception: the Egyptian fruit bat is a macrobat that uses echolocation — but it doesn't use the same method: scientists think that instead of using its larynx, it clicks using its nasal passages and the back of its tongue.
3. Microbats lack a claw on the second finger of their forelimb.
4. Megabats never have tails, but some species of microbats do.
5. Microbats have ears with a special organ that seems to be crucial in echolocation, and their ears are larger than megabats'.
6. Megabats have larger eyes.

The picture was taken by Michael Cleary, who wrote:

A Grey Headed Flying Fox having dipped coming straight at me, you can see the reflection in its eyes. Hope people don't mind me putting a few more flying Fox photos on, we are getting to the hot part of summer where they drink during the day.

For more, read the conversation on my G+ post, where Irina T. gave a nice answer to the puzzle.

January 13, 2018

Chopping a square into 7 triangles with almost the same area

It's impossible to divide a square into an odd number of triangles with the same area. This amazing result was proved by Paul Monsky in 1970, but I only heard about it today, from David Eppstein.

So it's impossible. But you can still try your best! These are the two best tries with 7 triangles and at most 8 vertices. These were discovered last year by Jean-Philippe Labbé, Güter Rote, and Günter Ziegler. They used a lot of clever math and programming to do this.

What do they mean by "best"? They mean that the standard deviation of the area of the triangles is as small as possible. For these two it's 0.0008051.

They couldn't check all the ways that used more than 8 vertices — it took too much time!

This was just the start of what Labbé, Rote and Ziegler did. They used a lot of clever math and programming to do this. David Eppstein summarized the rest:

According to Monsky's theorem, it is impossible to divide a square into an odd number of triangles, all the same area as each other. But if it can't be done exactly, how close to equal-area can you get? The answer is, at least superpolynomially close. The construction uses the Thue–Morse sequence to balance out the differences in area.

'Superpolynomially close' means that for any number \(p\), with \(n\) triangles you can get the difference in areas to be less than \(1/n^p\) if \(n\) is big enough.

Puzzle. Show that if n is even, you can divide a square into n triangles all having the same area.

This puzzle should be quite easy for most of you out there. How many seconds did it take you?

Here's the actual paper:

• Jean-Philippe Labbé, Güter Rote, and Günter Ziegler, Area difference bounds for dissections of a square into an odd number of triangles.

It's full of cool techniques... a great example of how even 'useless' and 'unimportant' problems in math can inspire interesting thoughts.

Here's the sketch of Monsky's proof, from Wikipedia:

1. Take the square to be the unit square with vertices at (0,0), (0,1), (1,0) and (1,1). If there is a dissection into n triangles of equal area then the area of each triangle is 1/n.
2. Color each point in the square with one of three colors, depending on the 2-adic valuation of its coordinates.
3. Show that a straight line can contain points of only two colors.
4. Use Sperner's Lemma to show that every triangulation of the square into triangles meeting edge-to-edge must contain at least one triangle whose vertices have three different colors.
5. Conclude from the straight-line property that a tricolored triangle must also exist in every dissection of the square into triangles, not necessarily meeting edge-to-edge.
6. Use Cartesian geometry to show that the 2-adic valuation of the area of a triangle whose vertices have three different colors is greater than 1. So every dissection of the square into triangles must contain at least one triangle whose area has a 2-adic valuation greater than 1.
7. If n is odd then the 2-adic valuation of 1/n is 1, so it is impossible to dissect the square into triangles all of which have area 1/n.

For more, including some answers to the puzzle, read the discussion on my G+ post.

For my March 2018 diary, go here.

home