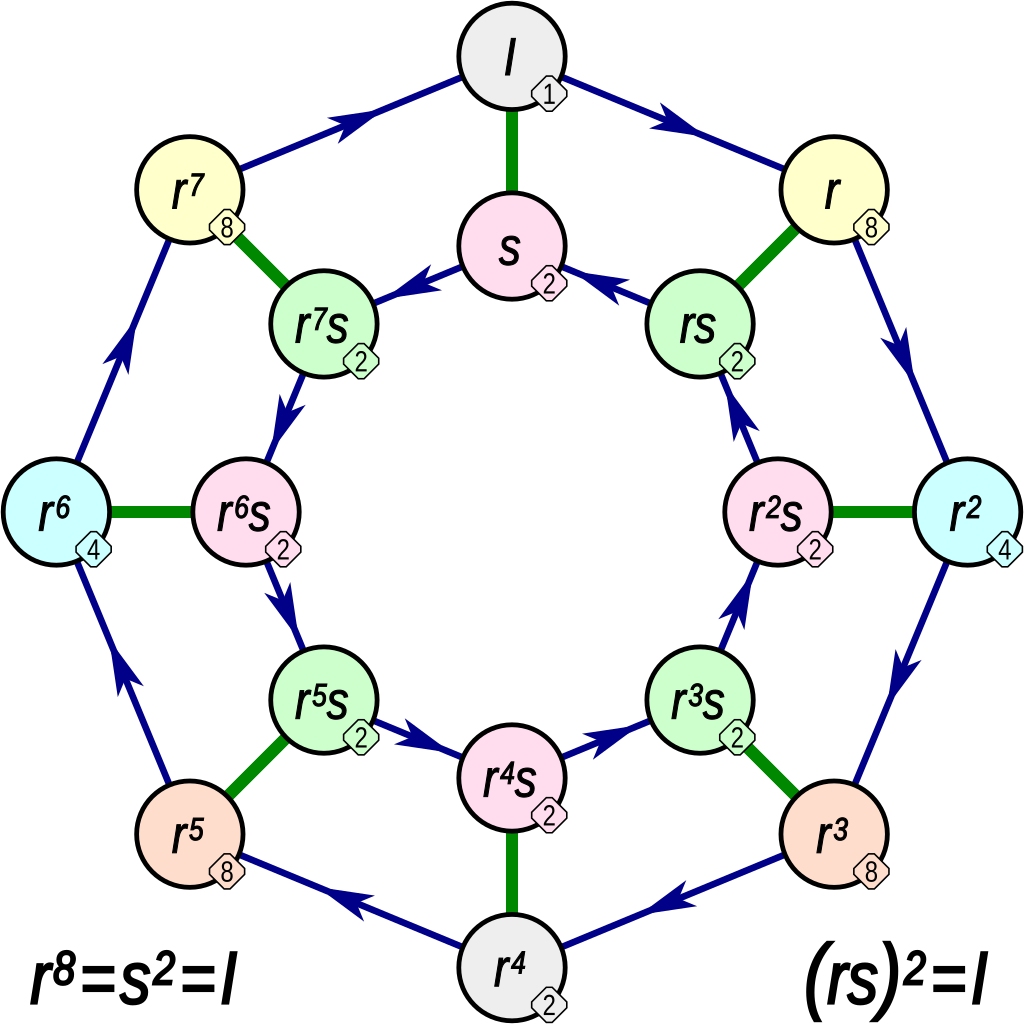

Take a regular octagon, like an American stop sign. It has a bunch of symmetries... and this is a picture of all its symmetries!
You can do nothing to it: that operation is called \(I\). You can rotate it an eighth of a turn clockwise: that's called \(r\). You can do that twice: that's called \(r^2\). And so on, up to \(r^7\). When you rotate your octagon an eighth of a turn 8 times it's back to where it started, so $$ r^8 = I $$ But you can also flip the sign over, say along the vertical axis. Let's call that operation \(s\). If you flip it over twice it's back to where it started, so $$ s^2 = I $$ There's another equation that's less obvious. Rotate your octagon an eighth of a turn clockwise, flip it over along the vertical axis, and then rotate it an eighth of a turn clockwise again. This is the same as just flipping it over: the two rotations cancel out! So $$ rsr = s $$ (The picture states this equation another way: \(rsrs = I\), or \((rs)^2 = I\) for short. It's equivalent.)
The picture shows all the different operations you can get by doing \(r\) and \(s\). There are only 16, namely these: $$ I, r, r^2, r^3, r^4, r^5, r^6, r^7 $$ and the 8 operations you get by rotating any amount and then flipping: $$ s, rs, r^2 s, r^3 s, r^4 s, r^5 s, r^6 s, r^7 s $$ In the picture, the arrows show what happens when you do another rotation r: for example there's an arrow from \(r^6\) to \(r^7\), or less obviously from rs to s because $$ rsr = s $$ The green lines show what happens when you do \(s\).
Finally, the little numbers say how many times you have to do an operation to get back to where you started! For example, if you rotate an octagon a quarter turn that's \(r^2\). If you do this 4 times you get back where you started, so the number next to \(r^2\) is 4.
Now I'll say the same stuff like a mathematician: we saw that the dihedral group with 16 elements, also called \(D_{16}\), has a presentation with generators \(r,s\) and relations $$ r^8 = s^2 = (rs)^2 = I. $$ We also saw its Cayley diagram, labeling each group element by its order.
Quicker, but fewer people will understand!
Now for something a bit less known. The group we just saw has an evil twin, another group with 16 elements, called the 'quasidihedral group'. Only one of the relations is different: now we have $$ srs = r^3 $$ This makes the Cayley diagram look like an 8-pointed star inside an octagon!
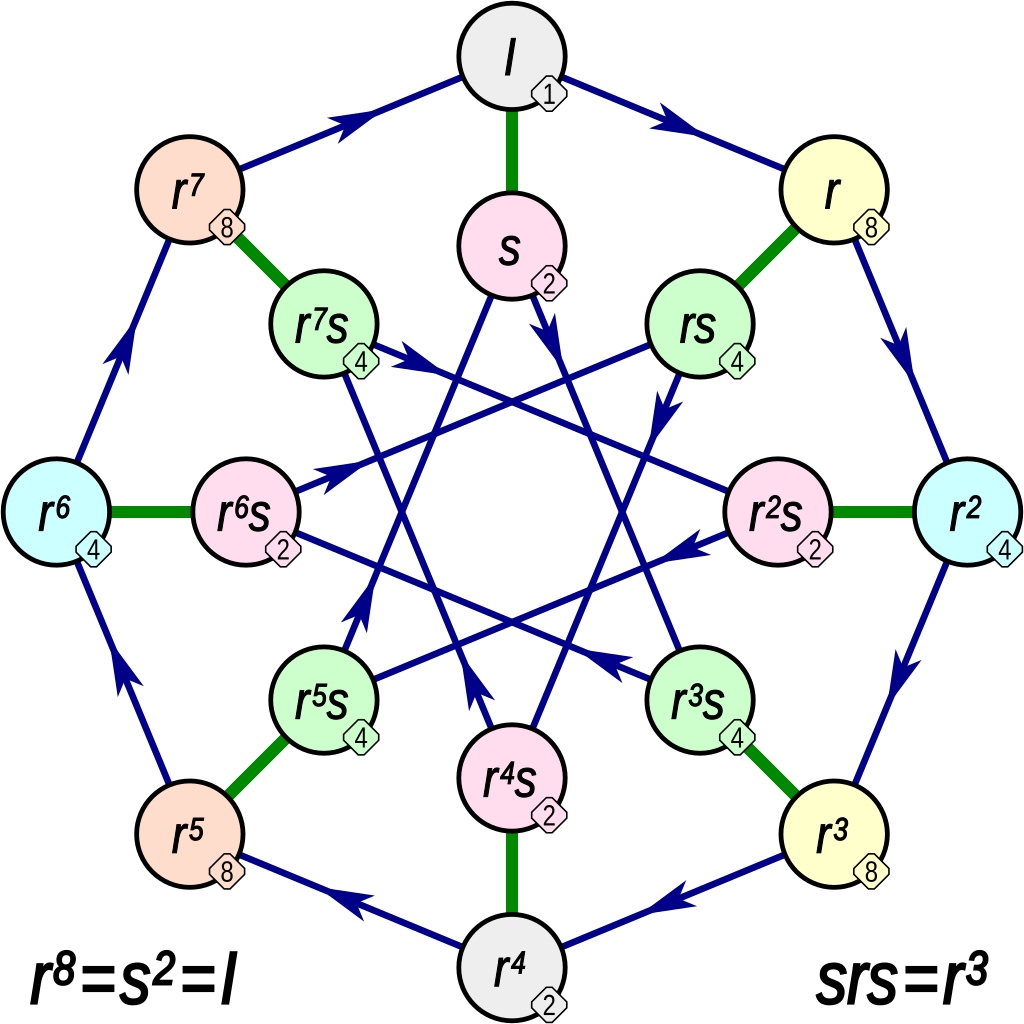
I heard about this group from Ian Agol, and I instantly looked it up on Wikipedia, where they have these nice pictures:
Once I was interested in the McGee graph, nicely animated here by Mamouka Jibladze:
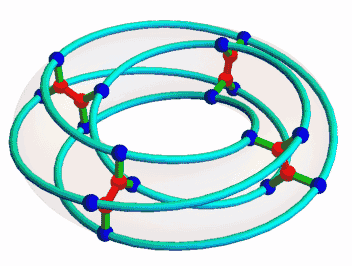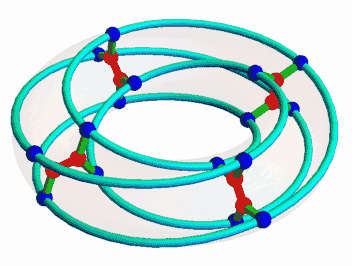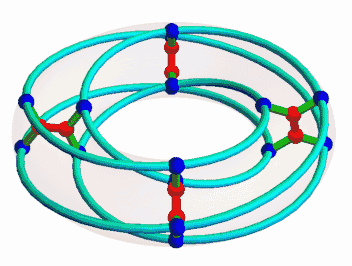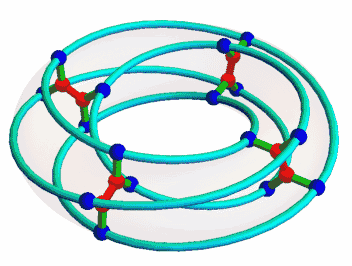
This is the unique (3,7)-cage, meaning a graph such that each vertex has 3 neighbors and the shortest cycle has length 7. Since it has a very symmetrical appearance, I hoped it would be connected to some interesting algebraic structures. But which?
I read on Wikipedia that the symmetry group of the McGee graph has order 32. Let's call it the McGee group. Unfortunately there are many different 32-element groups — 51 of them, in fact! — and the article didn't say which one this was. (It does now.)
I posted a general question:
and Gordon Royle said the McGee group is "not a super-interesting group, it is SmallGroup(32,43) in either GAP or Magma". Knowing this let me look up the McGee group on this website, which is wonderfully useful if you're studying finite groups:
There I learned that the McGee group is the so-called holomorph of the cyclic group \(\mathbb{Z}/8\): that is, the semidirect product of \(\mathbb{Z}/8\) and its automorphism group:
$$ \text{Aut}(\mathbb{Z}/8) \ltimes \mathbb{Z}/8 $$
I resisted getting sucked into the general study of holomorphs, or what happens when you iterate the holomorph construction. Instead, I wanted a more concrete description of the McGee group.
\(\mathbb{Z}/8\) is not just an abelian group: it's a ring! Since multiplication in a ring distributes over addition, we can get automorphisms of the group \(\mathbb{Z}/8\) by multiplying by those elements that have multiplicative inverses. These invertible elements form a group
$$ (\mathbb{Z}/8)^\times = \{1,3,5,7\} $$
called the multiplicative group of \(\mathbb{Z}/8\). In fact these give all the automorphisms of the group \(\mathbb{Z}/8\).
In short, the McGee group is
$$ (\mathbb{Z}/8)^\times \ltimes \mathbb{Z}/8 $$
This is very nice, because this is the group of all transformations of \(\mathbb{Z}/8\) of the form
$$ x \mapsto g x + a \qquad g \in (\mathbb{Z}/8)^\times , \; a \in \mathbb{Z}/8 $$
If we think of \(\mathbb{Z}/8\) as a kind of line — called the 'affine line over \(\mathbb{Z}/8\)' — these are precisely all the affine transformations of this line. Thus, the McGee group deserves to be called
$$ \text{Aff}(\mathbb{Z}/8) = (\mathbb{Z}/8)^\times \ltimes \mathbb{Z}/8 $$
This suggests that we can build the McGee graph in some systematic way starting from the affine line over \(\mathbb{Z}/8\). This turns out to be a bit complicated, because the vertices come in two kinds. That is, the McGee group doesn't act transitively on the set of vertices. Instead, it has two orbits, shown as red and blue dots here:
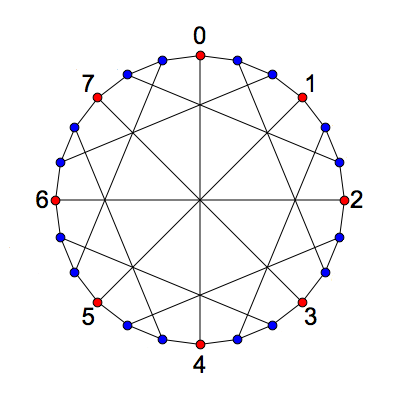
The 8 red vertices correspond straightforwardly to the 8 points of the affine line, but the 16 blue vertices are more tricky. There are also the edges to consider: these come in three kinds! Greg Egan figured out how this works, and I wrote it up:
Then a decade passed.
I didn't doubt this for a second. To paraphrase what Hardy said when he received Ramanujan's first letter, nobody would have the balls to make up this shit. So, I posed a challenge to find such an exotic outer automorphism:
By reading around, I soon learned that people have studied this subject quite generally:
An automorphism \(f \colon G \to G\) is class-preserving if for each \(g \in G\) there exists some \(h \in G\) such that
$$ f(g) = h g h^{-1} $$
If you can use the same \(h\) for every \(g\) we call \(f\) an inner automorphism. But some groups have class-preserving automorphisms that are not inner! These are the class-preserving outer automorphisms.
I don't know if class-preserving outer automorphisms are good for anything, or important in any way. They mainly just seem intriguingly spooky. An outer automorphism that looks inner if you examine its effect on any one group element is nothing I'd ever considered. So I wanted to see an example.
Rising to my challenge, Greg Egan found a nice explicit formula for some class-preserving outer automorphisms of the McGee group.
As we've seen, any element of the McGee group is a transformation
$$ x \mapsto g x + a \qquad g \in (\mathbb{Z}/8)^\times , \; a \in \mathbb{Z}/8 $$
so let's write it as a pair \((g,a)\). Greg Egan looked for automorphisms of the McGee group that are of the form
$$ f(g,a) = (g, a + D(g))$$
for some function
$$ D \colon (\mathbb{Z}/8)^\times \to \mathbb{Z}/8 $$
It is easy to check that \(f\) is an automorphism if and only if
$$ D(g g') = D(g) + g D(g') $$
Moreover, \(f\) is an inner automorphism if and only if
$$ D(g) = g b - b $$
for some \(b \in \mathbb{Z}/8\).
Now comes something cool noticed by Joshua Grochow: these formulas are an instance of a general fact about group cohomology!
Suppose we have a group \(G\) acting as automorphisms of an abelian group \(A\). Then we can define the cohomology \(H^n(G,A)\) to be the group of \(n\)-cocycles modulo \(n\)-coboundaries. We only need the case \(n = 1\) here. A 1-cocycle is none other than a function \(D \colon G \to A\) obeying $$ D(g g') = D(g) + g D(g') $$ while a 1-coboundary is one of the form $$ D(g) = g b - b $$ for some \(b \in A\). You can check that every 1-coboundary is a 1-cocycle. \(H^1(G,A)\) is the group of 1-cocycles modulo 1-coboundaries.
In this situation we can define the semidirect product \(G \ltimes A\), and for any \(D \colon G \to A\) we can define a function $$ f \colon G \ltimes A \to G \ltimes A$$ by $$ f(g,a) = (g, a + D(g)) $$
Now suppose \(G = \text{Aut}(A)\) and suppose \(G\) is abelian. Then by straightforward calculations we can check:
and
When \(A = \mathbb{Z}/8\) then \(G = \text{Aut}(A)\) is abelian and \(G \ltimes A\) is the McGee group. This puts Egan's idea into a nice context. But we still need to actually find maps \(D\) that give outer automorphisms of the McGee group, and then find class-preserving ones. I don't know how to do that using general ideas from cohomology. Maybe someone smart could do the first part, but the 'class-preserving' condition doesn't seem to emerge naturally from cohomology.
Anyway, Egan didn't waste his time with such effete generalities: he actually found all choices of \(D \colon (\mathbb{Z}/8)^\times \to \mathbb{Z}/8\) for which
$$ f(g,a) = (g, a + D(g)) $$
is a class-preserving outer automorphism of the McGee group. Namely:
$$ \begin{array}{ccl} (D(1), D(3), D(5), D(7)) &=& (0, 0, 4, 4) \\ (D(1), D(3), D(5), D(7)) &=& (0, 2, 0, 2) \\ (D(1), D(3), D(5), D(7)) &=& (0, 4, 4, 0) \\ (D(1), D(3), D(5), D(7)) &=& (0, 6, 0, 6) \end{array} $$
Last Saturday after visiting my aunt in Santa Barbara I went to Berkeley to visit the applied category theorists at the Topos Institute. I took a train, to lessen my carbon footprint a bit. The trip took 9 hours — a long time, but a beautiful ride along the coast and then through forests and fields.
The day before taking the train, I discovered my laptop was no longer charging! So, I bought a pad of paper. And then, while riding the train, I checked by hand that Egan's first choice of \(D\) really is a cocycle, and really is not a coboundary, so that it defines an outer automorphism of the McGee group. Then — and this was fairly easy — I checked that it defines a class-preserving automorphism. It was quite enjoyable, since I hadn't done any long calculations recently.
One moral here is that interesting ideas often arise from the interactions of many people. The results here are not profound, but they are certainly interesting, and they came from online conversations with Greg Egan, Gordon Royle, Joshua Grochow, the mysterious person who instantly knew that the McGee group was one of the two smallest groups with a class-preserving outer automorphism, and others.
But what does it all mean, mathematically? Is there something deeper going on here, or is it all just a pile of curiosities?
What did we actually do, in the end? Following the order of logic rather than history, maybe this. We started with a commutative ring \(A\), took its group of affine transformations \(\text{Aff}(A)\), and saw this group must have outer automorphisms if
$$ H^1(A^\times, A) \ne 0 $$
We saw this cohomology group really is nonvanishing when \(A = \mathbb{Z}/n\) and \(n = 8\). Furthermore, we found a class-preserving outer automorphism of \(\text{Aff}(\mathbb{Z}/8)\).
This raises a few questions:
I saw bit about the last question in this paper:
They say that this paper:
proves \(\text{Aff}(\mathbb{Z}/n)\) has a class-preserving outer automorphism when \(n\) is a multiple of 8.
Does this happen only for multiples of 8? Is this somehow related to the most famous thing with period 8 — namely, Bott periodicity? I don't know.