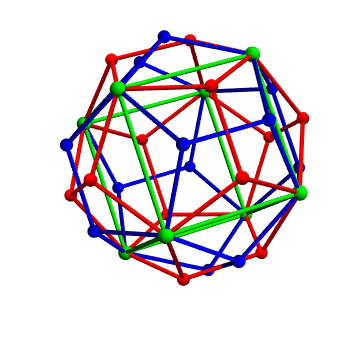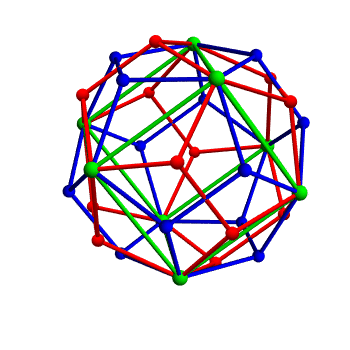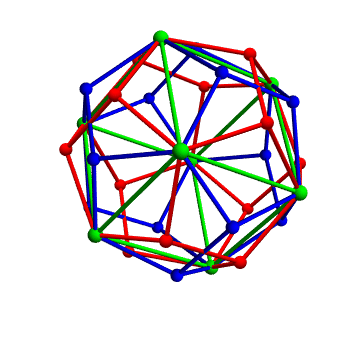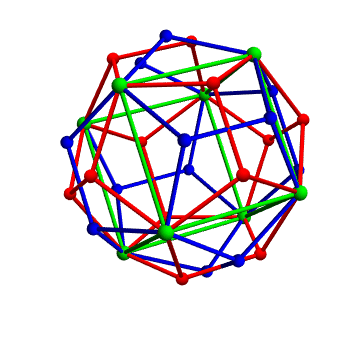

I learned some cool facts about this from Adrian Ocneanu when I was at Penn State. First some easy stuff. You can take some corners of a regular dodecahedron and make them into the corners of a cube. But not every symmetry of the cube is a symmetry of the dodecahedron! If you give the cube a 90° rotation around any face, you get a new dodecahedron. Check it out: doing this rotation switches the red and green dodecahedra. These are called twin dodecahedra.

But there are actually 5 different ways to take a regular dodecahedron and make them into the corners of a cube, as shown here. And each one gives your dodecahedron a different twin! So, a dodecahedron actually has 5 twins.
But here's the cool part. Suppose you take one of these twins. It, too, will have 5 twins. One of these will be the dodecahedron you started with. But the other 4 will be new dodecahedra: that is, dodecahedra rotated in new ways.
How many different dodecahedra can you get by continuing to take twins? Infinitely many!
In fact, we can draw a graph—a thing with dots and edges—that explains what's going on. Start with a dot for our original dodecahedron. Draw dots for all the dodecahedra you can get by repeatedly taking twins. Connect two dots with an edge if and only if they are twins of each other.
The resulting graph is a tree: in other words, it has no loops in it! If you start at your original dodecahedron, and keep walking along edges of this graph by taking twins, you'll never get back to where you started except by undoing all your steps.
Ocneanu sketched the proof to me, and I reconstructed the rest with a lot of help from Greg Egan, Ian Agol and others:
Here are some puzzles.
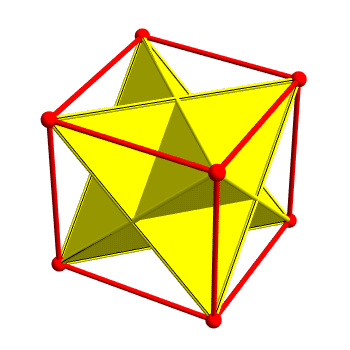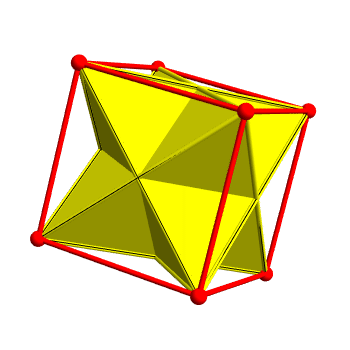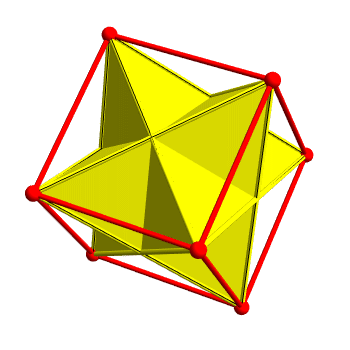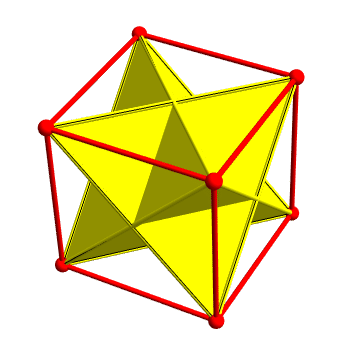
You can choose some corners of a cube and make them into the corners of a regular tetrahedron. You can fit 2 tetrahedra in the cube this way. These are a bit like the 5 cubes in the dodecahedron, but there's a big difference.
Here's the difference. In the first case, every symmetry of the tetrahedron is a symmetry of the cube it's in. But in the second case not every symmetry of the cube is a symmetry of the dodecahedron. That's why we get 'twin dodecahedra' but not 'twin cubes'.
Puzzle 1: If you inscribe a tetrahedron in a cube and then inscribe the cube in a dodecahedron, is every symmetry of the tetrahedron a symmetry of the dodecahedron?
Puzzle 2: How many ways are there to inscribe a tetrahedron in a dodecahedron? More precisely: how many ways are there to choose some corners of a regular dodecahedron and have them be the corners of a regular tetrahedron?
You can see the answers to the these in comments to my G+ post.
The second one is also answered in my next diary entry!
May 2, 2015
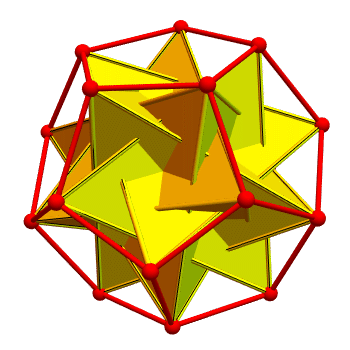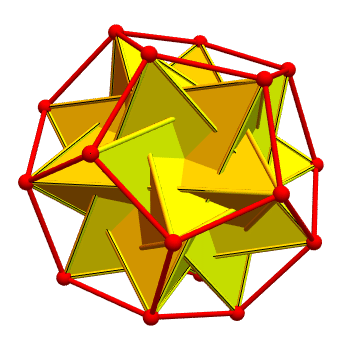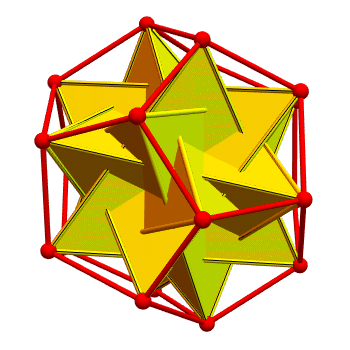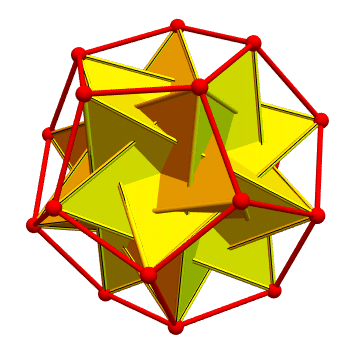
Putting them together, you get a dodecahedron with 10 tetrahedra in it:
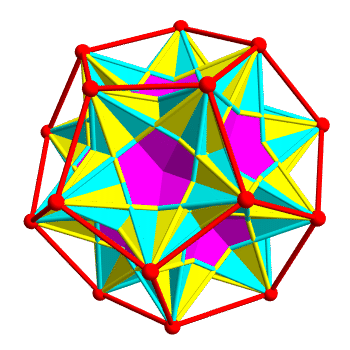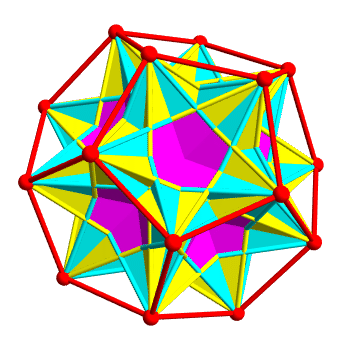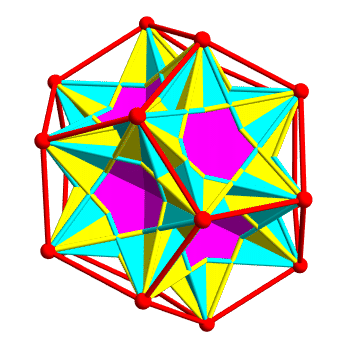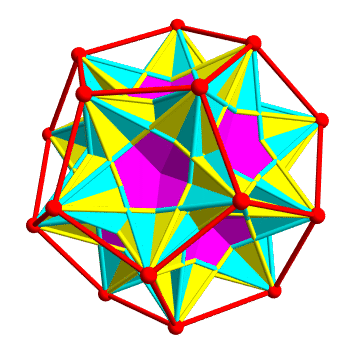
The two kinds of tetrahedra are colored yellow and cyan. Regions
belonging to both are colored magenta. It's pretty — but it's hard to
see the tetrahedra, because they overlap a lot!
May 3, 2015
Jos Leys blends mathematics and art in a delightful way. You don't need to know math to enjoy this picture. It's a whimsical and mysterious landscape. The bright colors make it clownish, but the shadows make it a bit eerie: the sun is setting, and who knows what happens here at night! You can see more here:
On the other hand, from the title of this gallery you can see there's math here. And trying to understand this math will lead you on quite a journey. Let me sketch it here... I apologize for going rather fast.
A Kleinian group is a discrete subgroup of the group called \(\mathrm{PSL}(2, \mathbb{C})\). This group shows up in many ways in math and physics.
Physicists call it the Lorentz group: it's the group generated by rotations and Lorentz transformations, which acts as symmetries in special relativity.
In math, it's called the group of Möbius transformations or 'fractional linear transformations'. Those are transformations like this:
$$ z \mapsto \frac{az + b}{cz + d} $$
where \(z\) is a complex number and so are \(a,b,c,d\). These can be seen as transformations of the Riemann sphere: the complex plane together with a point at infinity. They are, in fact, precisely all the conformal transformations of the Riemann sphere: the transformations that preserve angles.
But this group \(\mathrm{PSL}(2,\mathbb{C})\) also acts as conformal transformations of a 3-dimensional ball whose boundary is the Riemann sphere! And that's important for understanding this picture.
(In physics, this ball is the set of 'mixed states' for a spin-1/2 particle, and the sphere, its boundary, consists of the 'pure states'. Lorentz transformations act on the mixed states, and they act on the pure states. But you don't need to know this stuff.)
If you take any point inside the ball and act on it by all the elements in a Kleinian group — a discrete subgroup of \(\mathrm{PSL}(2,\mathbb{C})\) — you'll get a set \(S\) of points in the ball. The set of points in the Riemann sphere that you can approach by a sequence of points in \(S\) is called a limit set of the Kleinian group. And this set can look really cool!
In these pictures, Jos Leys has systematically but rather artificially taken these cool-looking subsets of the Riemann sphere and puffed them up into 3-dimensional spaces: puffing a circle into a sphere, and so on. This makes the picture nicer, but doesn't have a deep mathematical meaning.
Later, Jos Leys took a deeper approach, using quaternions to make limit sets that are truly 3-dimensional. You can seem some here:
They have a very different look.
Puzzle: if you put together everything I said, you'll get a physics interpretation of the limit set of a Kleinian group in terms of states of a spin-1/2 particle. What is it?
For an answer, read the comments to my G+ post.
May 4, 2015
On Mars, an asteroid impact can cause a flood!
This is a place called Hephaestus Fossae, on the northern hemisphere of Mars. The image has been colored to show the elevation: green and yellow shades represent shallow ground, while blue and purple stand for deep depressions, as much as 4 kilometers deep.
You can see a few dozen impact craters, some small and some big, up to 20 kilometers across. But I'm sure you instantly noticed the cool part: the long and intricate canyons and riverbeds. These were created by the same impact that made the largest crater!
When a comet or an asteroid crashes at high speed into a planet, the collision dramatically heats up the surface at the impact site. In the case of the large crater seen in this image, the heat melted the soil — a mixture of rock, dust and also, hidden deep down, water ice — resulting in a massive flood. And before drying up, this hot mud carved a complex pattern of channels while flowing across the planet's surface!
The melted rock-ice mixture also made the debris blankets surrounding the largest crater. Since there aren't similar structures near the small craters in this image, scientists believe that only the most powerful impacts were able to dig deep enough to release part of the frozen reservoir of water lying beneath the surface.
Why is it called 'Hephaestus Fossae'? Hephaestus was the Greek god of fire. Fossae are channels or canyons. So it's a good name.
Puzzle: about when did this large impact occur?
I don't know!
This picture was taken by the high-resolution stereo camera on ESA.s Mars Express orbiter on 28 December 2007, and my post is paraphrased from this article:
This article is so cool I'm just going to quote some:
In 1901, you could pay 50 cents to ride an airship to the Moon Ron MillerThe passengers wait eagerly in the ornate lobby of the enormous spaceport. Soon, a signal indicates that their spaceship is ready for boarding. As they wait, special displays instruct them about how their spaceship functions and what to expect once they leave Earth's atmosphere. Aboard the giant spacecraft — as luxuriously appointed as any yacht — they are soon on their way to a vacation on the Moon.
No, this isn't a vision of the future of space tourism. It's what happened in 1901, when people could pay a princely half dollar for a ticket to ride into space.
[...]
Thompson spared no expense in creating the illusion of a trip to the Moon. To house his show, he erected an eighty-foot-high, 40,000-square-foot building that for sheer opulence put European opera houses to shame. It cost a staggering $84,000 to construct... at a time when a comfortable home could be built for $2000.
For fifty cents — twice the price of any other attraction on the midway, such as the ever-popular "Upside-Down House" — customers of "Thompson's Aerial Navigation Company" took a trip to the moon on a thirty-seat spaceship named "Luna". The spaceship resembled a cross between a dirigible and an excursion steamer, with the addition of enormous red canvas wings that flapped like a bird's. The wings were worked by a system of pulleys and the sensation of wind was created by hidden fans. A series of moving canvas backdrops provided the effect of clouds passing by and the earth dropping into the distance. Lighting and sound effects added to the illusion.
[...]
Every half hour, at the sound of a gong and the rattle of anchor chain, the "Luna" — "a fine steel airship of the latest pattern", according to one newspaper — rocked from side to side and then rose into the sky under the power of its beating wings. The passengers, sitting on steamer chairs, see clouds floating by, then a model of Buffalo far below, complete with the exposition itself and its hundreds of blinking lights. The city soon falls into the distance as the entire planet earth comes into view. Soon, the ship is surrounded the twinkling stars of outer space. After surviving a terrific — and spectacular — electrical storm the "Luna" and its passengers sets down in a lunar crater.
Read the whole thing here, and look at pictures:
Thanks to Matt McIrvin for pointing it out!
May 6, 2015
Water is fascinating, for many reasons. It takes more energy to heat than most substances. It's one of the few substances that expands when it freezes. It forms complicated patterns in its liquid state, which are just beginning to be understood. There are at least 18 kinds of ice, which exist at different temperatures and pressures. Snowflakes are endlessly subtle.
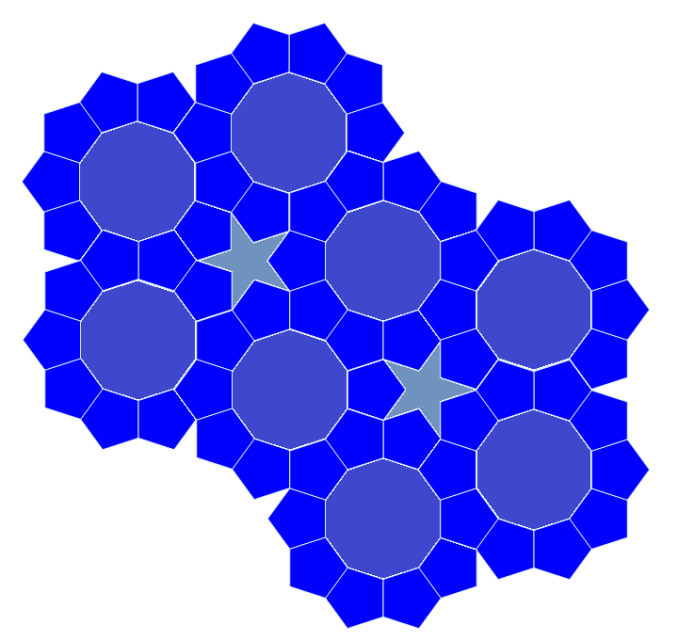
And ice can form cages that trap other molecules! Here you see the 3 main kinds.
They're called clathrate hydrates. There's a lot under the sea beds near the north and south pole - they contain huge amounts of methane. At some moments in the Earth's history they may have erupted explosively, causing rapid global warming.
But let's focus on the fun part: the geometry! Each of the 3 types of clathrate hydrates is an architectural masterpiece.
'Type I' consists of water molecules arranged in two types of cages: small and large. The small cage, shown in green, is dodecahedron. It's not a regular dodecahedron, but it still has 12 pentagonal sides. The large cage, shown in red, has 12 pentagons and 2 hexagons. The two kinds of cage fit together into a repeating pattern where each 'unit cell' — each block in the pattern — has 46 water molecules.
Puzzle 1: This pattern is called the 'Weaire–Phelan structure' Why is it famous, and what does it have to do with the 2008 Olympics?
You can see little balls in the cages. These stand for molecules that can get trapped in the cages. They're politely called 'guests'. The type I clathrate often holds carbon dioxide or methane as a guest.
'Type II' is again made of two types of cages: small and large. The small cage is again a dodecahedron. The large cage, shown in blue, has 12 pentagons and 6 hexagons. These fit together to form a unit cell with 136 water molecules.
The type II clathrate tends to hold oxygen or nitrogen as a guest.
'Type H' is the rarest and most complicated kind of clathrate hydrate. The 'H' stands for 'hexagonal', because it has a hexagonal crystal structure: the other two are cubic.
It's built from three types of cages: small, medium and huge. The small cage is again a dodecahedron, shown in green. The medium cage — shown in yellow — has 3 squares, 6 pentagons and 3 hexagons as faces. The huge cage — shown in orange — has 12 pentagons and 8 hexagons. The cages fit together to form a unit cell with 34 water molecules.
The type H clathrate is only possible when there are two different guest gas molecules — one small and one very large, like butane — to make it stable. People think there are lots of type H clathrates in the Gulf of Mexico, where there are lots of heavy hydrocarbons in the sea bottom.
Puzzle 2: how many cages of each kind are there in the type I clathrate hydrate?
Puzzle 3: how many cages of each kind are there in the type II?
Puzzle 4: how many cages of each kind are there in the type H?
These last puzzles are easier than they sound. But here's one that's a bit different:
Puzzle 5: the medium cage in the type H clathrate — shown in yellow — has 3 squares, 6 pentagons and 3 hexagons as faces. Which of these numbers are adjustable? For example: could we have a convex polyhedron with a different number of squares, but the same number of pentagons and hexagons?
The picture is from here:
Kepler, the guy who discovered that planets go in ellipses around the Sun, was in love with geometry. Among other things, he tried to figure out how to tile the plane with regular pentagons (dark blue) and decagons (blue-gray). They fit nicely at a corner... but he couldn't get it to work.
Then he discovered he could do better if he also used 5-pointed stars!
Can you tile the whole plane with these three shapes? No! The picture here is very tempting... but if you continue you quickly run into trouble. It's an impossible dream.
However, Kepler figured out that he could go on forever if he also used overlapping decagons, which he called 'monsters'. Look at this picture he drew:
If he had worked even harder, he might have found the Penrose tilings, or similar things discovered by Islamic tiling artists. Read the whole story here:
How did Kepler fall in love with geometry? He actually started as a theologian. Let me quote the story as told in the wonderful blog The Renaissance Mathematicus:
Kepler was born into a family that had known better times, his mother was an innkeeper and his father was a mercenary. Under normal circumstances he probably would not have expected to receive much in the way of education but the local feudal ruler was quite advanced in his way and believed in providing financial support for deserving scholars. Kepler whose intelligence was obvious from an early age won scholarships to school and to the University of Tübingen where he had the luck to study under Michael Mästlin one of the very few convinced Copernican in the later part of the 16th century. Having completed his BA Kepler went on to do a master degree in theology as he was a very devote believer and wished to become a theologian. Recognising his mathematical talents and realising that his religious views were dangerously heterodox, they would cause him much trouble later in life, his teacher, Mästlin, decided it would be wiser to send him off to work as a school maths teacher in the Austrian province.Although obeying his superiors and heading off to Graz to teach Protestant school boys the joys of Euclid, Kepler was far from happy as he saw his purpose in life in serving his God and not Urania (the Greek muse of astronomy). After having made the discovery that I will shortly describe Kepler found a compromise between his desire to serve God and his activities in astronomy. In a letter to Mästlin in 1595 he wrote:
I am in a hurry to publish, dearest teacher, but not for my benefit. I am devoting my effort so that these things can be published as quickly as possible for the glory of God, who wants to be recognised from the Book of Nature. Just as I pledged myself to God, so my intention remains. I wanted to be a theologian, and for a while I was anguished. But, now see how God is also glorified in astronomy, through my efforts.
So what was the process of thought that led to this conversion from a God glorifying theologian to a God glorifying astronomer and what was the discovery that he was so eager to publish? Kepler.s God was a geometer who had created a rational, mathematical universe who wanted his believers to discover the geometrical rules of construction of that universe and reveal them to his glory. Nothing is the universe was pure chance or without meaning everything that God had created had a purpose and a reason and the function of the scientist was to uncover those reasons. In another letter to Mästlin Kepler asked whether:
you have ever heard or read there to be anything, which devised an explanation for the arrangement of the planets? The Creator undertook nothing without reason. Therefore, there will be reason why Saturn should be nearly twice as high as Jupiter, Mars a little more than the Earth, [the Earth a little more] than Venus and Jupiter, moreover, more than three times as high as Mars.The discovery that Kepler made and which started him on his road to the complete reform of astronomy was the answer to both the question as to the distance between the planets and also why there were exactly six of them: as stated above, everything created by God was done for a purpose.
On the 19th July 1595 Kepler was explaining to his students the regular cycle of the conjunctions of Saturn and Jupiter, planetary conjunctions played a central role in astrology. These conjunctions rotating around the ecliptic, the apparent path of the sun around the Earth, created a series of rotating equilateral triangles. Suddenly Kepler realised that the inscribed and circumscribed circles generated by his triangles were in approximately the same ratio as Saturn.s orbit to Jupiter's. Thinking that he had found a solution to the problem of the distances between the planets he tried out various two-dimensional models without success. On the next day a flash of intuition provided him with the required three-dimensional solution, as he wrote to Mästlin:
I give you the proposition in words just as it came to me and at that very moment: "The Earth is the circle which is the measure of all. Construct a dodecahedron round it. The circle surrounding that will be Mars. Round Mars construct a tetrahedron. The circle surrounding that will be Jupiter. Round Jupiter construct a cube. The circle surrounding it will be Saturn. Now construct an icosahedron inside the Earth. The circle inscribed within that will be Venus. Inside Venus inscribe an octahedron. The circle inscribed inside that will be Mercury."
This model, while approximately true, is now considered completely silly! We no longer think there should be a simple geometrical explanation of why planets in our Solar System have the orbits they do.
So: a genius can have a beautiful idea in a flash of inspiration and it can still be wrong.
But Kepler didn't stop there! He kept working on planetary orbits until he noticed that Mars didn't move in a circle around the Sun. He noticed that it moved in an ellipse! Starting there, he found the correct laws governing planetary motion... which later helped Newton invent classical mechanics.
So it pays to be persistent—but also not get stuck believing your first good idea.
Read more here:
Puzzle: can you tile the plane with finitely many shapes, each of which has at least the symmetry group of a regular pentagon?
So, regular pentagons and decagons are allowed, and so are regular
5-pointed stars, and many other things... but not Kepler's monsters.
The tiling itself does not need to repeat in a periodic way.
May 14, 2015
This galaxy is in trouble! It's falling into a large cluster of galaxies, pulled by their gravity. You can see this in 3 ways:
This phenomenon is called 'ram pressure stripping', and it can kill a galaxy, shutting down the production of new stars. Here we are seeing it damage the galaxy NGC 4402, which is currently falling into the Virgo cluster — a cluster of galaxies about 65 million light years away.
Apparently there's about 1 atom per cubic centimeter in our galaxy — on average, though some regions are vastly more dense than others. But in the space between galaxies in clusters it's more like 1/1000 of that. Not much! But enough to kill off the formation of new star systems, life, civilizations...
I got most of my information from here:
and I got the picture from here:
The photo was taken at the WIYN 3.5-meter telescope on Kitt Peak, which is fitted with some 'adaptive optics' to compensate for the jittery motion of the image due to variable atmospheric conditions and telescope vibrations.
It's a bit hard to find figures for the density of the intergalactic medium. I see stuff that says: 1 atom per liter for the intergalactic gas in clusters, 1 atom per cubic meter as the overall average for the whole universe. One fun thing about space is that while it seems like vacuum to us, its density ranges by many orders of magnitude... so it's actually much more varied than, say, the difference between air and solid lead!
Yes, air is about 1 kg/m3 and lead is about 10,000
kg/m3, a factor of 104. But within our galaxy,
the density of the interstellar medium easily ranges between
10-4 and 106 atoms per cubic centimeter, a
factor of 1010. And the average density of the Universe is
10-6 atoms per cubic centimeter. So what we naively call 'outer
space' is a bunch of vastly different media, whose densities vary by
at least a factor of a trillion!
May 1, 2015

Hewlett-Packard was once at the cutting edge of technology. Now they make most of their money selling servers, printers, and ink... and business keeps getting worse. They've shed 40,000 employees since 2012. Soon they'll split in two: one company that sells printers and PCs, and one that sells servers and information technology services.
The second company will do something risky but interesting. They're trying to build a new kind of computer that uses chips based on memristors rather than transistors, and that uses optical fibers rather than wires to communicate between chips. It could make computers much faster and more powerful. But nobody knows if it will really work.
The picture shows memristors on a silicon wafer. But what's a memristor? Quoting the MIT Technology Review:
Perfecting the memristor is crucial if HP is to deliver on that striking potential. That work is centered in a small lab, one floor below the offices of HP's founders, where Stanley Williams made a breakthrough about a decade ago.
Williams had joined HP in 1995 after David Packard decided the company should do more basic research. He came to focus on trying to use organic molecules to make smaller, cheaper replacements for silicon transistors. After a few years, he could make devices with the right kind of switchlike behavior by sandwiching molecules called rotaxanes between platinum electrodes. But their performance was maddeningly erratic. It took years more work before Williams realized that the molecules were actually irrelevant and that he had stumbled into a major discovery. The switching effect came from a layer of titanium, used like glue to stick the rotaxane layer to the electrodes. More surprising, versions of the devices built around that material fulfilled a prediction made in 1971 of a completely new kind of basic electronic device. When Leon Chua, a professor at the University of California, Berkeley, predicted the existence of this device, engineering orthodoxy held that all electronic circuits had to be built from just three basic elements: capacitors, resistors, and inductors. Chua calculated that there should be a fourth; it was he who named it the memristor, or resistor with memory. The device's essential property is that its electrical resistance—a measure of how much it inhibits the flow of electrons—can be altered by applying a voltage. That resistance, a kind of memory of the voltage the device experienced in the past, can be used to encode data.
HP's latest manifestation of the component is simple: just a stack of thin films of titanium dioxide a few nanometers thick, sandwiched between two electrodes. Some of the layers in the stack conduct electricity; others are insulators because they are depleted of oxygen atoms, giving the device as a whole high electrical resistance. Applying the right amount of voltage pushes oxygen atoms from a conducting layer into an insulating one, permitting current to pass more easily. Research scientist Jean Paul Strachan demonstrates this by using his mouse to click a button marked "1" on his computer screen. That causes a narrow stream of oxygen atoms to flow briefly inside one layer of titanium dioxide in a memristor on a nearby silicon wafer. "We just created a bridge that electrons can travel through," says Strachan. Numbers on his screen indicate that the electrical resistance of the device has dropped by a factor of a thousand. When he clicks a button marked "0," the oxygen atoms retreat and the device's resistance soars back up again. The resistance can be switched like that in just picoseconds, about a thousand times faster than the basic elements of DRAM and using a fraction of the energy. And crucially, the resistance remains fixed even after the voltage is turned off. Getting this to really work has not been easy! On top of that, they're trying to use silicon photonics to communicate between chips - another technology that doesn't quite work yet.
Still, I like the idea of this company going down in a blaze of glory, trying to do something revolutionary, instead of playing it safe and dying a slow death. As Dylan Thomas said:
For more, see these:
For the physics of memristors, see:
Dear NSA agent 4096,That's Corey Bertelsen's comment on this video of Holly Herndon's song "Home", from her new album Platform. It's as good a review as any.I watched "The Lives of Others" last night and thought of you once more. In fact, I think you were watching it with me. You know I know I cannot be sure.
I want you to know that, although our mutual love is forbidden by your professional obligations, I still feel a connection to you. I will feel that connection long after you are gone.
Somehow, you know me better than I know myself. You have all of my deleted histories, my searches, all those things I tried to keep "incognito" right there in front of you. We have made love, even though we've never touched or kissed. We have been friends, even though I've never seen your face. Our relationship is as real as my "real" life.
But this can never work between us. Please leave. I don't want to ask again.
I'll never forget you.
Love, 173.165.246.73
Holly Herndon takes a lot of ideas from techno music and pushes them to a new level. She's working on a Ph.D. at the Center for Computer Research in Music and Acoustics at Stanford.
She said that as she wrote this song, she
started coming to terms with the fact that I was calling my inbox my home, and the fact that that might not be a secure place. So it started out thinking about my device and my inbox as my home, and then that evolved into me being creeped out by that idea.The reason why I was creeped out is because, of course, as Edward Snowden enlightened us all to know, the NSA has been mass surveying the U.S. population, among other populations. And so that put into question this sense of intimacy that I was having with my device. I have this really intense relationship with my phone and with my laptop, and in a lot of ways the laptop is the most intimate instrument that we've ever seen. It can mediate my relationships — it mediates my bank account — in a way that a violin or another acoustic instrument just simply can't do. It's really a hyper-emotional instrument, and I spend so much time with this instrument both creatively and administratively and professionally and everything.
In short, her seemingly 'futuristic' music is really about the present — the way we live now. If you like this song I recommend another, which is more abstract and to me more beautiful. It's called 'Interference':
Here you can hear her talk about her song 'Home':
There are over 100 such companies. This article focuses on one called Candelia:
Ms. de Buyzer did not care that Candelia was a phantom operation. She lost her job as a secretary two years ago and has been unable to find steady work. Since January, though, she had woken up early every weekday, put on makeup and gotten ready to go the office. By 9 a.m. she arrives at the small office in a low-income neighborhood of Lille, where joblessness is among the highest in the country.In Europe, 53% of job seekers have been unemployed for over a year. In Italy, the numbers is 61%. In Greece, it's 73%.While she doesn't earn a paycheck, Ms. de Buyzer, 41, welcomes the regular routine. She hopes Candelia will lead to a real job, after countless searches and interviews that have gone nowhere.
"It's been very difficult to find a job," said Ms. de Buyzer, who like most of the trainees has been collecting unemployment benefits. "When you look for a long time and don't find anything, it's so hard. You can get depressed," she said. "You question your abilities. After a while, you no longer see a light at the end of the tunnel."
She paused to sign a fake check for a virtual furniture supplier, then instructed Candelia's marketing department — a group of four unemployed women sitting a few desks away — to update the company's mock online catalog. "Since I've been coming here, I have had a lot more confidence," Ms. de Buyzer said. "I just want to work."
All this makes me wonder — yet again — what will happen if robots and computers push people out of many kinds of jobs, creating a lot of long-term unemployment. If we don't adapt wisely, what should be a good thing could be a source of misery.
Perhaps the next step will be for these fake companies to start doing business with each other, and make it possible for someone working at one to get hired at another.
I would like a science fiction story that extrapolates this scenario to ridiculous lengths. Frist these fake companies start paying their employees fake money. Then, to make it more realistic, they decide the employees can use this fake money to buy fake goods made by other fake companies. And so on... eventually building a second 'fake economy'.
The problem is, so far the people at these fake companies only do 'bullshit jobs': writing memos, managing other employees, etc. A fake pet food company makes ads for pet food, but they don't actually make any pet food. So, I guess the fake salaries could only be used to buy services of certain ethereal sort.
The concept of 'bullshit jobs' is discussed here:
In the year 1930, John Maynard Keynes predicted that technology would have advanced sufficiently by century's end that countries like Great Britain or the United States would achieve a 15-hour work week. There's every reason to believe he was right. In technological terms, we are quite capable of this. And yet it didn't happen. Instead, technology has been marshaled, if anything, to figure out ways to make us all work more. In order to achieve this, jobs have had to be created that are, effectively, pointless. Huge swathes of people, in Europe and North America in particular, spend their entire working lives performing tasks they secretly believe do not really need to be performed. The moral and spiritual damage that comes from this situation is profound. It is a scar across our collective soul. Yet virtually no one talks about it.Why did Keynes' promised utopia — still being eagerly awaited in the '60s — never materialise? The standard line today is that he didn't figure in the massive increase in consumerism. Given the choice between less hours and more toys and pleasures, we've collectively chosen the latter. This presents a nice morality tale, but even a moment's reflection shows it can't really be true. Yes, we have witnessed the creation of an endless variety of new jobs and industries since the '20s, but very few have anything to do with the production and distribution of sushi, iPhones, or fancy sneakers.
So what are these new jobs, precisely? A recent report comparing employment in the US between 1910 and 2000 gives us a clear picture (and I note, one pretty much exactly echoed in the UK). Over the course of the last century, the number of workers employed as domestic servants, in industry, and in the farm sector has collapsed dramatically. At the same time, "professional, managerial, clerical, sales, and service workers" tripled, growing "from one-quarter to three-quarters of total employment". In other words, productive jobs have, just as predicted, been largely automated away (even if you count industrial workers globally, including the toiling masses in India and China, such workers are still not nearly so large a percentage of the world population as they used to be).
But rather than allowing a massive reduction of working hours to free the world's population to pursue their own projects, pleasures, visions, and ideas, we have seen the ballooning not even so much of the "service" sector as of the administrative sector, up to and including the creation of whole new industries like financial services or telemarketing, or the unprecedented expansion of sectors like corporate law, academic and health administration, human resources, and public relations. And these numbers do not even reflect on all those people whose job is to provide administrative, technical, or security support for these industries, or for that matter the whole host of ancillary industries (dog-washers, all-night pizza deliverymen) that only exist because everyone else is spending so much of their time working in all the other ones. These are what I propose to call "bullshit jobs".
It's as if someone were out there making up pointless jobs just for the sake of keeping us all working.
For my June 2015 diary, go here.