
The Kōetsu utai-bon is the text for the Japanese nō play Bashō by Komparu Zenchiku. It is one of several editions produced by the wealthy Kyoto merchant Suminokura Soan around 1607. It's said that these books "represent an astonishing leap, something unprecedented in the history of the illustrated or decorated book: this was the first time a book had been conceived as a single unified work of art."
And back then, Hamilton felt he had to argue for the importance of studying point particles in classical mechanics.

These are called the Hamilton-Jacobi equations, and \(W\) is called Hamilton's principal function. I wish classical mechanics books explained them better! They fit naturally into the wave picture of classical particle mechanics, where the particle has amplitude $$\psi(x,t,x',t') = \exp(iW(x,t,x',t')/\hbar) $$ to get from \((x,t)\) to \((x',t')\). Momentum and energy describe the \(x\) and \(t\) derivatives of \(\psi\), just as in quantum mechanics.
I bet Hamilton and Jacobi came up with their ideas when trying to reconcile the classical mechanics of particles to optics, as part of the long-running argument about whether light was a particle or a wave. In quantum mechanics we learned it's both.
But in fact, already in classical mechanics of ordinary particles we
have an equivalence between the well-known 'particle picture' where a
particle traces out a least-action path, and the 'wave picture' I've
just described. I want to understand this better.
May 13, 2021
I enjoyed this editorial:
The most curious subplot in the news right now is the admission, at the most senior levels of the United States government, that the military services have collected visuals, data and testimonials recording flying objects they cannot explain; that they are investigating these phenomena seriously; and that they will, in the coming months, report at least some of their findings to the public. It feels, at times, like the beginning of a film where everyone is going about their lives, even as the earthshaking events unfurl on a silenced television in the background.Unlike some, I feel no urge to thump my fist on the table and insist that obviously these unidentified flying objects aren't extraterrestrials. Nor am I suggesting they are! I'm just interested to see how this plays out.
Except for one thing: flute players need to breathe! It's an endless succession of 16th notes with no rests. How could he be so dumb?
I was looking for a performance by a flutist who'd mastered circular breathing and could avoid the awkward pauses as they gasp for breath. But then I found this: an explanation of what Bach was actually up to!
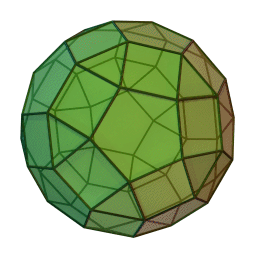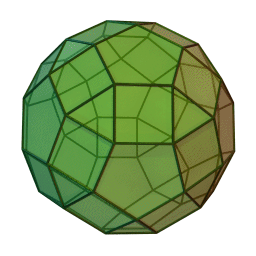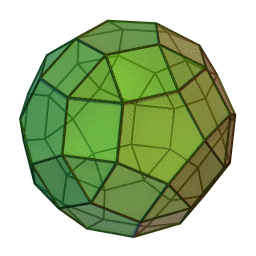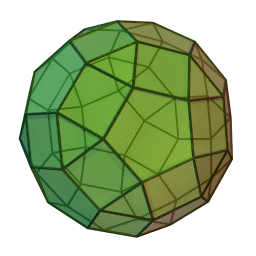
A polyhedron doesn't look like a smooth manifold but it almost is. If you remove the vertices, the rest is naturally a smooth manifold. In fact it's a smooth Riemannian manifold with a flat metric!
The point is that a folded piece of paper is naturally a smooth flat Riemannian manifold: it's just mapped into 3d space in a way that's not smooth at the fold.
So a polyhedron is a smooth flat Riemannian manifold on the faces and edges, just not the vertices.
At the vertices of a polyhedron there are 'conical singularities', meaning that if you add up the angles around a vertex you don't get \(2\pi\). Just like the tip of a cone!
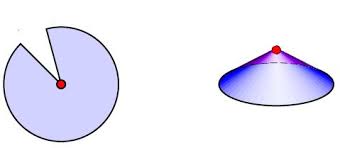
So, a polyhedron gives the smooth 2-sphere a flat Riemannian metric except at a finite set of points, with a conical singularity at each of these points! Let me call this a 'flat cone sphere'.
Suppose we have a flat cone sphere where the total angle at each conical singularity is \(\lt 2 \pi\). Then this cone sphere comes from a unique convex polyhedron! This theorem was proved by Alexandrov in 1942.
But what does all this have to do with quantum gravity?
In 3d general relativity with massive point particles, you can take space to be a surface with a flat Riemannian metric except at the particles, where you get conical singularities. A flat cone sphere is an example!
So, 3d quantum gravity is about polyhedra.
May 22, 2021
The 'sphericon'. If you roll
it on the floor, every single point touches the floor at some time.
It was discovered by a carpenter named Colin Roberts in 1969, but
patented by someone else in 1980.
May 23, 2021
Say you know the roots of a polynomial \(P\) and you want to know the
roots of its derivative. You can do it using physics!
Namely, electrostatics in 2d space, viewed as the complex plane.
To keep things simple, let us assume \(P\) does not have repeated roots. Then the procedure works as follows.
Put equal point charges at each root of \(P\), then see where the resulting electric field vanishes. Those are the roots of \(P'\).
We can use this trick to see something cool. There's no way the electric field can vanish outside the convex hull of your set of point charges. After all, the electric field must point out of that region. So, the roots of \(P'\) must lie in the convex hull of the roots of \(P\)!
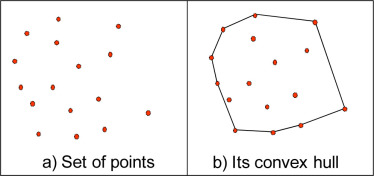
This cool fact is called the Gauss–Lucas theorem. It always seemed mysterious to me. Now, thanks to this 'physics proof', it seems completely obvious!
Of course, it relies on my first claim: that if we put equal point charges at the roots of \(P\), the electric field they generate will vanish at the roots of \(P'\). Why is this true?
By multiplying by a constant if necessary, we can assume $$ P(z) = \prod_{i = 1}^n (z - a_i) $$ Thus $$ \ln |P(z)| = \sum_{i = 1}^n \ln|z - a_i| $$ This is the electric potential created by equal point charges at the points \(a_i\) in the complex plane. The corresponding electric field is the gradient of \( \ln|P(z)| \), so it vanishes at the critical points of this function. Equivalently, it vanishes at the critical points of the exponential of this function, namely \(|P(z)|\). Apart from one exception mentioned below, these are just the critical points of \(P\), namely the roots of \(P'\).
The exception occurs when \(P\) has a critical point that is also a root of \(P\). \(|P|\) is not smooth where \(P\) vanishes, so in this case we cannot say the critical point of \(P\) is a critical point of \(|P|\).
However, when \(P\) has a critical point that is also a root of of \(P\), this point is a repeated root, and I already said I'm assuming \(P\) has no repeated roots. (The case where \(P\) has repeated roots is also easy.)
For more, read my article:
Similarly, in category theory we don't only do colimits: we do 'weighted' colimits.
In a colimit we have a diagram in a category \(C\), described as a functor \(F\colon D \to C\). Then we 'add up' all the objects \(F(d) \in C\) in a subtle way to get an object of \(C\).
In fact this process involves summing (coproduct) but also modding out (coequalizer).
So, a better way to think of it is that we 'glue together' all the objects \(F(d) \in C\) to get a new object of \(C\), the colimit of \(F\colon D \to C\). But this colimit is a generalization of a sum.
Similarly, a 'weighted colimit' is a generalization of a weighted sum. To do a weighted colimit, we need not only a diagram \(F\colon D \to C\) but also a 'weight', which is a functor \(W\colon D^{\textrm{op}} \to \mathrm{Set}\). The weight says 'how many times we should count each object in our diagram'. Now the weight is a set, not a number!
I won't say how you do a weighted colimit: there are textbooks that say, and tweets are not so good for this.
Let me just give a cool example that's on my mind today. A weight \(W\colon D^{\textrm{op}} \to \mathrm{Set}\) is also called a 'presheaf' on \(D\). Can we do something with that? Yes!
We can try to take the weighted colimit of the 'identity diagram' \(1\colon D \to D\) with the weight \(W\colon D^{\textrm{op}} \to \mathrm{Set}\), where \(W\) is any presheaf on \(D\).
The identity diagram is a huge diagram that looks exactly like the category it's in! So, taking the weighted colimit of \(1\colon D \to D\) with weight \(W\colon D^{\textrm{op}} \to \mathrm{Set}\) is like gluing together all the objects of \(D\), using \(W(d)\) copies of each object \(d\).
This weighted colimit may not exist. But if it does for all \(W\), we get something really cool. It gives a systematic way of turning presheaves on \(D\) into objects on D. And this turns out to be a left adjoint to the Yoneda embedding!
Recall that the Yoneda embedding turns objects of \(D\) into presheaves on \(D\). Each object \(d \in D\) gives the presheaf \(\mathrm{hom}(-,d) \colon D^{\textrm{op}} \to \mathrm{Set}\).
A left adjoint to the Yoneda embedding, if it exists, turns presheaves on \(D\) back into objects of \(D\), by gluing together \(W(d)\) copies of each object \(d\).
A category is called total if its Yoneda embedding has a left adjoint. The left adjoint is then always given by a weighted colimit as I explained.
Lots of famous categories are total: \(\mathrm{Set}, \mathrm{Grp}, \mathrm{Vect}\), etc. Indeed, the category of algebras of any monad on \(\mathrm{Set}\) is total. And total categories have lots of nice properties! For example, total categories always have all colimits — because totality says it's really easy to glue together lots of objects in your category.
Even better, any colimit-preserving functor from a total category to any small category is a left adjoint.
What's the best place to learn more about weighted colimits? I'm not sure — I picked this stuff up on the street.

For total categories this article is good: