When a big star runs out of fuel, its core collapses and its outer layers explode into space. If it's not too big, its core becomes a big ball of neutrons. And if the resulting neutron star is spinning fast and emitting lots of radiation from its north and south magnetic poles, we call it a pulsar. It's called that because you see a pulse of radiation as it spins.
A pulsar is an amazing thing. Imagine something twice as heavy as our Sun, only 20 kilometers across, spinning around 1000 times a second, shooting out beams of radiation!
Now, imagine a planet near a pulsar: a dead world raked by intense radiation. It would be a strange, intensely alien place.
But in fact, the first planets to be discovered outside our solar system were pulsar planets! The reason is that pulsars keep time very accurately: the pulses are like the ticks of a clock. By detecting slight irregularities, we can tell if a pulsar is getting pulled back and forth by an orbiting planet.
In 1992, Aleksander Wolszczan and Dale Frail found the first planets outside our solar system: two planets orbiting a pulsar named PSR B1257+12. One is 4 times as heavy as the Earth, and it orbits the pulsar every 66 days. The other is just a bit heavier than the Earth, and it orbits every 99 days.
It seems these planets were formed from the debris of a companion star that used to orbit the pulsar. This star would have been destroyed by the huge explosion that formed the pulsar, called a supernova.
There's another pulsar planet that's very different. It's very close to a pulsar named PSR J1719-1438. It's so close that its orbit would fit inside our Sun, and it orbits the pulsar once every two hours.
It seems to have the mass of Jupiter, but a diameter just 4 times that of our Earth. If so, it must be extremely dense: a bit more dense than platinum!
What could it be? People think it's the remains of a white dwarf star whose outer layers were blasted away by the supernova that formed the pulsar. If so, it could be made mostly of carbon and oxygen — leftover elements that the white dwarf wasn't able to burn.
In fact, it might even be similar to an enormous high-density diamond, so it's been nicknamed 'The Diamond Planet'. But nobody is sure, and these days people think it contains too much oxygen.
The picture here is from NASA, and it's an artist's impression of the
planets orbiting PSR 1257+12.
November 3, 2015
You are trapped on Pluto. Your only hope of survival is traveling a long distance to an old base where there is still a working rocket.
Your rover is insulated against the amazingly cold temperatures, and its huge corrugated metal wheels have no trouble driving over the ice — which is mostly made of frozen nitrogen.
But then you come to a large pit. It's about 10 meters deep and 100 meters across. Its walls are not very steep, so you can cross it, but it's a bit annoying.
Then you come to another pit. And another, and another.
You have entered Sputnik Planum, a huge field of ice pits in a plain named after the old Russian satellite Sputnik.
We don't know how these pits formed. They may be caused by sublimation where ice turns directly into gas as it warms up in the chilly Plutonian summer. They may start small and grow over time. But why are they here, and not all over Pluto?
Many of these pits are connected, forming troughs that line up. Why? We don't know.
Good luck. Maybe you will find out. If you survive, maybe you can tell us.
For more, see:
There are over 15 kinds of ice. Different kinds are stable at different pressures and temperatures. Some of the weirdest may exist inside 'ice giants': planets like Uranus and Neptune, which have also been found orbiting other stars. Most of what we know about these kinds of ice comes from computer simulations, since they only exist at very high pressures.
They're called 'superionic ices', because while the oxygen atoms get locked in a crystal structure, the hydrogen atoms become ionized, breaking apart into protons and electrons. The protons can then move around like a liquid between the oxygen atoms!
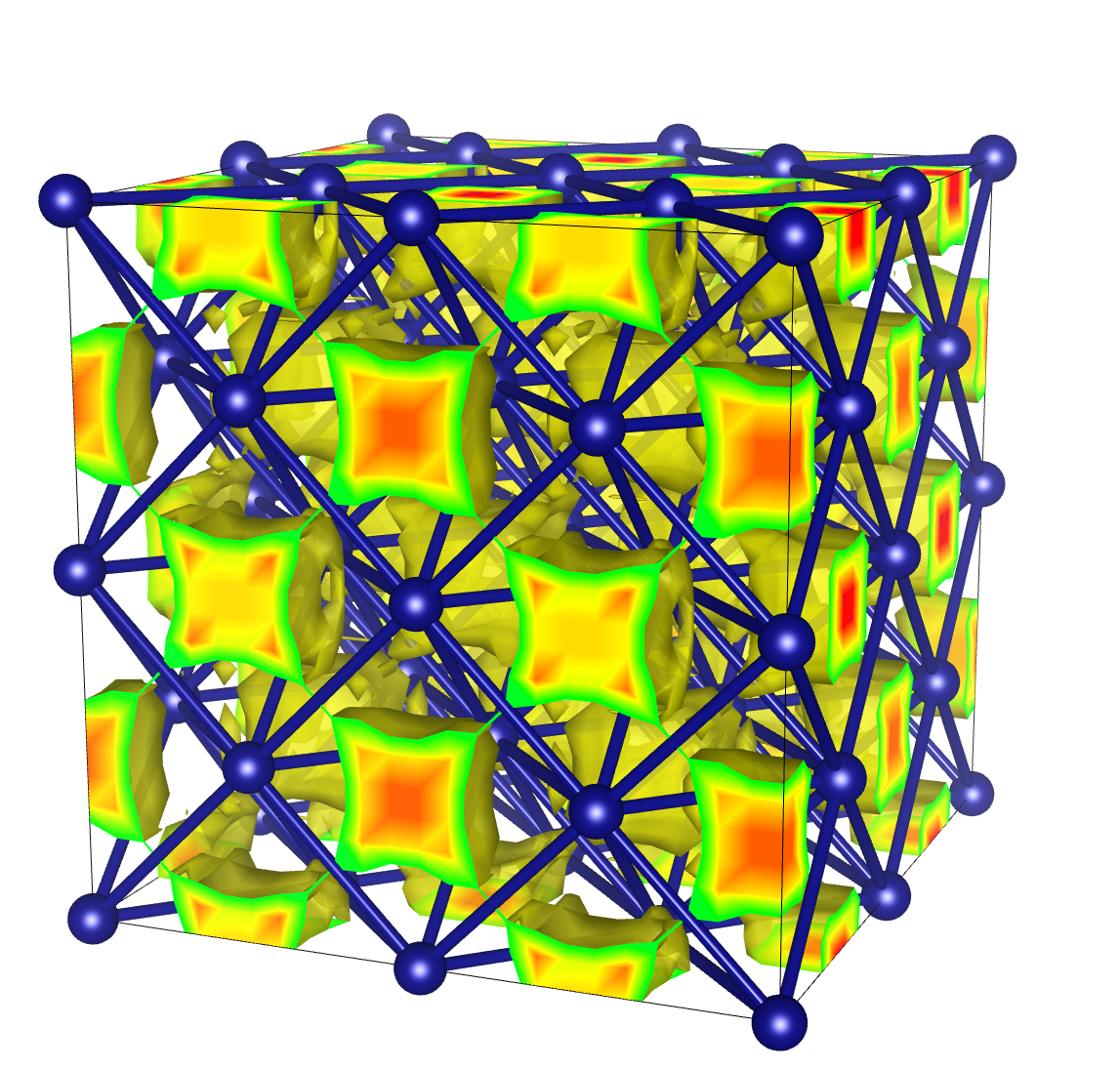
The first phase of superionic ice was predicted in 1999 by a group of Italian scientists. They predicted that this ice exists at pressures 500,000 times the atmospheric pressure here on Earth, and temperatures of a few thousand Kelvin. In this kind of ice, the oxygen atoms form a crystal called a body centered cubic:
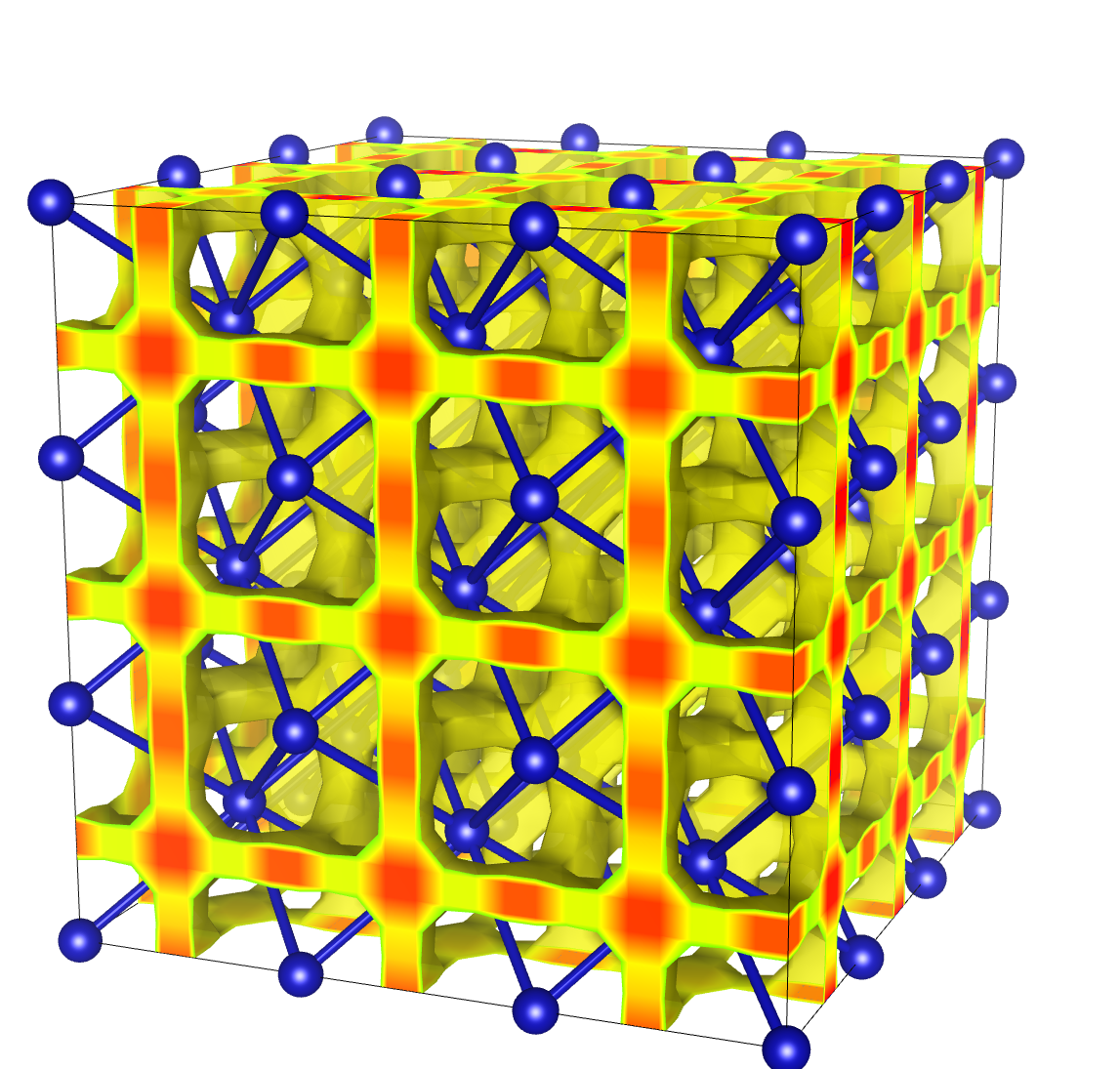
In 2012, Hugh F. Wilson, Michael L. Wong, and Burkhard Militzer predicted the new phase shown at the top of this diary entry. This may show up above 1,000,000 times atmospheric pressure. The oxygen atoms, shown as blue spheres, form a pattern called a face centered cubic. The protons are likely to be found in the orange regions.
Hugh Wilson, who apparently drew the pictures of both forms of ice, said:
Superionic water is a fairly exotic sort of substance. The phases of water we're familiar with all consist of water molecules in various arrangements, but superionic water is a non-molecular form of ice, where hydrogen atoms are shared between oxygens. It's somewhere between a solid and a liquid.the hydrogen atoms move around freely like in a liquid, while the oxygens stay rigidly fixed in place. It would probably flow more like a liquid, though, since the planes of oxygen atoms can slide quite freely against one another, lubricated by the hydrogens.
These simulations are hard, and newer papers are reporting different results. You can also try to make superionic ice in the lab, but that's even harder! In 2005 Laurence Fried tried to make it at the Lawrence Livermore National Laboratory in California. He smashed water molecules between diamond anvils while simultaneously zapping it with lasers. He seemed to find evidence for superionic ice.
Eventually theory and experiment will converge on the truth. Only then will we understand the hearts of the ice giants.
You can read more here:
and for some even newer results, try this:
Here's the paper on the first kind of superionic ice:

In fact we can make atoms almost like hydrogen, but 1/186 times as big across. Unfortunately they only last 2 microseconds. But that's still long enough for them to form molecules, and for us to do chemical experiments with them. Chemists have gotten really good at this stuff.
The trick is to take the electron in a hydrogen atom and replace it with a muon. This is a particle 207 times heavier than an electron, but otherwise very similar. Unfortunately a muon has a half-life of just 2 microseconds: then it decays into an electron and some other crud.
Why is an ordinary hydrogen atom the size it is, anyway? It's the uncertainty principle. The atom is making its energy as small as possible while remaining consistent with the uncertainty principle.
A hydrogen atom is made of an electron and a proton. If it were bigger, its potential energy would increase, because the electron would be further from the proton. So, the atom 'wants to be small'. And without quantum mechanics to save it, it would collapse down to a point: The Incredible Shrinking Atom.
But if the atom were smaller, you'd know the position of its particles more precisely &mash; so the uncertainty principle says you'd know their momentum less precisely. They'd be wiggling around more wildly and unpredictably So the kinetic energy would, on average, be higher.
So there's a tradeoff! Too big means lots of potential energy. Too small means lots of kinetic energy. Somewhere in the middle is the best — and you can use this to actually calculate how big a hydrogen atom is!
But what if you could change the mass of the electron? This would change the calculation. It turns out that making electrons heavier would make atoms smaller!
While we can't make electrons heavier, we can do the next best thing: use muons.
Muonic hydrogen is a muon orbiting a proton. It's like an atom, but much smaller than usual, so it does weirdly different things when it meets an ordinary atom. It's a whole new exotic playground for chemists.
And, you can do nuclear fusion more easily if you start with smaller atoms! It's called 'muon-catalyzed fusion', and people have really done it. The only problem is that it takes a whole lot of energy to make muons, and they don't last long. So, it's not practical — it doesn't pay off. At least not yet. Maybe we just need a few more brilliant ideas:
In my October 11th entry I talked about a version of hydrogen where we keep the electron and replace the proton by a positively charged antimuon. That's called muonium. Muonium is lighter than ordinary hydrogen but almost the same size, just a tiny bit bigger. It's chemically almost the same as hydrogen, except that it decays in 2 microseconds.
With muonic hydrogen it's the reverse: it's a lot smaller, but it's just a bit heavier. It's chemically very different from ordinary hydrogen.
If you do the calculation, you can show that the radius of a
hydrogen-like atom is proportional to
$$ mM/(m+M) $$
where \(m\) is the mass of the lighter particle and \(M\) is the mass
of the heavier one. If we say an electron has mass 1, then a muon has
mass 207 and a proton has mass 1836. You can use this formula to see
that muonic hydrogen has a radius 1/186 as big as ordinary hydrogen,
while muonium has a radius 1.004 times as big.
November 22, 2015
I've been staying at home for the last two days writing a paper about information and entropy in biological systems. My wife is away, and I'm trying to keep distractions to a bare minimum, trying to get into that state where I'm completely absorbed, there's always something to do, and it's lots of fun. That's what I love about writing. At first I feel stuck, frustrated. But gradually the ideas start falling into place - and once they do, I don't want to be anywhere else!
This state is called flow, and it's great. But life can't be all flow, it seems.
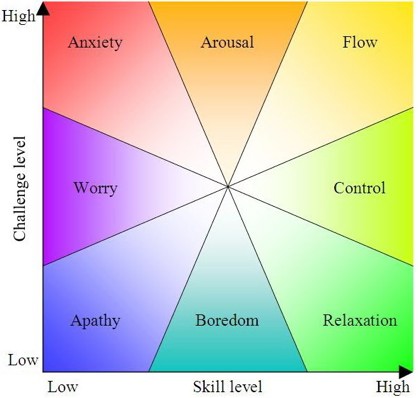
I like this chart. I like any chart that takes psychology and maps it down to a few axes in a reasonably plausible way. I don't have to 'believe in it' to enjoy a neat picture that pretends to tame the wild mess of the soul.
Apparently this chart goes back to Mihály Csikszentmihélyi's theory of flow. According to Wikipedia:
In his seminal work, Flow: The Psychology of Optimal Experience, Csikszentmihályi outlines his theory that people are happiest when they are in a state of flow. a state of concentration or complete absorption with the activity at hand and the situation. It is a state in which people are so involved in an activity that nothing else seems to matter. The idea of flow is identical to the feeling of being in the zone or in the groove. The flow state is an optimal state of intrinsic motivation, where the person is fully immersed in what he is doing. This is a feeling everyone has at times, characterized by a feeling of great absorption, engagement, fulfillment, and skill.and during which temporal concerns (time, food, ego-self, etc.) are typically ignored.In an interview with Wired magazine, Csikszentmihályi described flow as "being completely involved in an activity for its own sake. The ego falls away. Time flies. Every action, movement, and thought follows inevitably from the previous one, like playing jazz. Your whole being is involved, and you're using your skills to the utmost."
Csikszentmihályi characterized nine component states of achieving flow including "challenge-skill balance, merging of action and awareness, clarity of goals, immediate and unambiguous feedback, concentration on the task at hand, paradox of control, transformation of time, loss of self-consciousness, and autotelic experience".
What does autotelic mean? It seems to mean 'internally driven', as opposed to seeking external rewards. Csikszentmihályi says "An autotelic person needs few material possessions and little entertainment, comfort, power, or fame because so much of what he or she does is already rewarding." Anyway, back to the Wikipedia article:
To achieve a flow state, a balance must be struck between the challenge of the task and the skill of the performer. If the task is too easy or too difficult, flow cannot occur. Both skill level and challenge level must be matched and high; if skill and challenge are low and matched, then apathy results.
But in this chart, 'apathy' is just one of 8 options, the one diametrically opposite to 'flow'. I like the idea of how 'relaxation' is somewhere between flow and boredom, but I'm not sure it feels next to 'control'.
It's all very thought-provoking. We have these different modes, or moods, and we bounce between them without very much thought about what they're for and what's the overall structure of the space of these moods.
Moods seem like the opposite of mathematics and logic, but there's
probably a science of moods which we haven't fully understood yet - in
part because when we're in a mood, it dominates us and prevents us
from thinking about it analytically.
November 30, 2015
Ever since I was a kid, I've loved the ways you could tile the plane with regular polygons. Some are used for floor tiles — pondering these is a great way to stay entertained while sitting in public restrooms. But unfortunately, a lot of the fancier ones have not come into wide use.
There are 3 regular tilings: you can use equal-sized regular triangles, squares or hexagons to tile the plane. If you let yourself use several kinds of regular polygons in the same tiling but demand that every vertex look alike, you get 8 more choices: the uniform tilings.
Only recently did I learn about the k-uniform tilings, where you relax a bit and let there be k different kinds of vertices.
The picture shows a 4-uniform tiling. There are 2 different kinds of vertices where
They are different in this way: no symmetry of the whole tiling can carry the first to the second. So, while they look the same right at the vertex, further away they look different.
Puzzle 1: can you see the 2 kinds in both cases? Can you describe why they're different?
According to the experts, there are 20 2-uniform tilings. There are 61 3-uniform tilings. There are 151 4-uniform tilings. There are 332 5-uniform tilings. There are 673 6-uniform tilings. And I guess the list stops there only because people got tired!
This picture was drawn by Tom Ruen. You can find it, along with lots more, here:
Puzzle 2: what uniform tiling is this 4-uniform tiling based on, and how?
For Tom Ruen's answer to Puzzle 2, see the conversation on my G+ post.