The singularity

But we get much more!
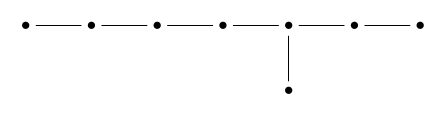
It turns out every Γ-invariant polynomial on ℂ² is a polynomial in V, E, and F.

Thus, the variety ℂ²/Γ is isomorphic to the complex surface

{(V, E, F) ∈ ℂ³ : V⁵ + E² + F³ = 0}

This surface is smooth except at V = E = F = 0, where it has a singularity.

And hiding in this singularity is E₈!

For more on this 'Kleinian singularity', see Section 5 here:

Peter Slodowy, Platonic solids, Kleinian singularities, and Lie groups, in Algebraic Geometry, Springer, Berlin, 1983, pp. 102–138.

and Section 5.1 here:

For much more, see:

Klaus Lamotke, Regular Solids and Isolated Singularities, Vieweg & Sohn, Braunschweig, 1986.