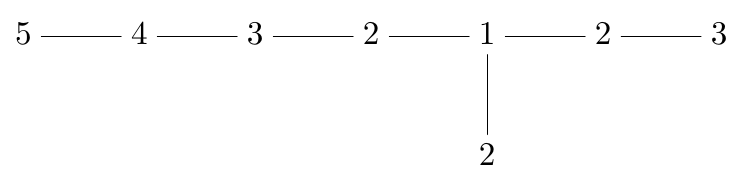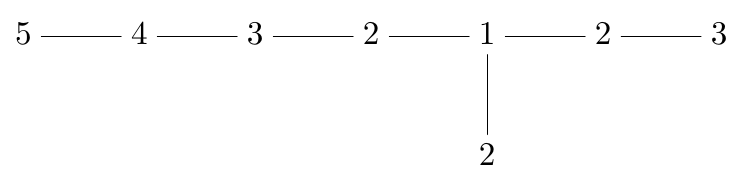Duval's work


This amazing fact was discovered by Patrick Du Val in 1934. Why is it true? I'll just mention some clues.
The E8 Dynkin diagram:
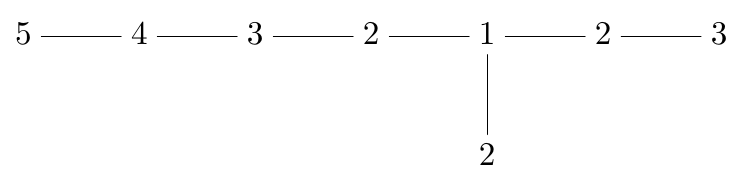
is closely connected to the relation between the three Γ-invariant polynomials on ℂ2:
V5 + E2 + F3 = 0
and also this group presentation:
Γ = ⟨v, e, f | v5 = e2 = f 3 = vef ⟩
For an introduction to these matters, see sections 6-7 here:
- Peter Slodowy, Platonic solids, Kleinian singularities, and Lie groups, in Algebraic Geometry, Springer, Berlin, 1983, pp. 102–138.
and sections 5-7 here:
For full details, see:
-
Klaus Lamotke, Regular Solids and Isolated Singularities, Vieweg & Sohn, Braunschweig, 1986.
The group A5 has this presentation:
⟨v, e, f | v5 = e2 = f 3 = vef = 1⟩
where:
-
v is a 1/5 turn around some vertex,
-
e is a 1/2 turn around the center of an edge touching that vertex,
-
f is a 1/3 turn around the center of a face touching that vertex,
and we need to choose the sense of the rotations correctly to get vef = 1. Similarly, the group Γ has this presentation:
⟨v, e, f | v5 = e2 = f 3 = vef ⟩
The two-to-one map from Γ to A5 sends the element v5 = e2 = f 3 = vef to 1, since this element describes a 360° rotation.