

Next: Special Relativity, Spinors, and the Dirac Equation
Up: Loose Ends
Can one reconstruct the Lie group from the Lie
algebra? In general, the multiplication table of a group is determined if
you know the multiplication table for its generators; why not try this
with the ``infinitesimal'' generators?
If you try this approach, you will find you need to know the commutators of
infinitesimal elements, like
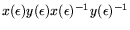 .
.
My ``definition'' of the Lie algebra involved approximating infinitesimal
generators by Taylor expansions out to the first order. In other words, I
used only first order derivatives. But to the first order, the commutators
are zero!
Say we approximate an ``infinitesimal'' element of the Lie group
out to the second order:
If you work out the commutator, you will find expressions of the form
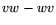 appearing, where
appearing, where 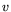 and
and 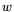 belong to the Lie algebra. And one
can verify that
belong to the Lie algebra. And one
can verify that 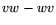 belongs in fact to the Lie algebra, as I've defined
it, although
belongs in fact to the Lie algebra, as I've defined
it, although 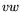 and
and 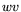 in general don't.
in general don't.
Remarkably, knowledge of these second order terms completely specifies the
structure of the Lie group near the identity. That is, if the Lie algebras
are isomorphic, then the Lie groups are locally isomorphic. Third and
higher-order terms are not needed.


Next: Special Relativity, Spinors, and the Dirac Equation
Up: Loose Ends
© 2001 Michael Weiss