

Up: Loose Ends
Previous: Special Relativity, Spinors, and The Dirac Equation
The spin-statistics theorem of quantum
field theory says that particles with half-odd-integer spin (like the
electron) must be fermions, while particles with integer spin (like the
photon) must be bosons. Fermions obey Fermi-Dirac statistics, and hence
obey the Pauli exclusion principle. Bosons obey Bose-Einstein statistics.
The difference in statistics stems from the properties of the exchange
operator. This is a unitary operator, say 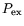 , which
represents the effect of exchanging two identical fermions, or two
identical bosons. For the fermion case, one has at a critical point in the
calculations
, which
represents the effect of exchanging two identical fermions, or two
identical bosons. For the fermion case, one has at a critical point in the
calculations
and for the boson case,
The minus sign for fermions ultimately derives from the double covering of
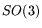 via
via 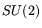 . Spinors also get into the act. Since I don't fully
understand the story myself, this seems like a good place to stop.
. Spinors also get into the act. Since I don't fully
understand the story myself, this seems like a good place to stop.


Up: Loose Ends
Previous: Special Relativity, Spinors, and The Dirac Equation
© 2001 Michael Weiss
For more on the spin-statistics theorem, try
this.
![]() , which
represents the effect of exchanging two identical fermions, or two
identical bosons. For the fermion case, one has at a critical point in the
calculations
, which
represents the effect of exchanging two identical fermions, or two
identical bosons. For the fermion case, one has at a critical point in the
calculations