vectors in 3-space |
We have two fundamental concepts that are easy to visualize:
vectors in 3-space |
The rotation group acts on the space of vectors. For any representation of the rotation group and any representation of the vector space, we would like to have an intuitive grasp of the action. (Since the action preserves distances, one can also consider the action of the group just on the set of vectors of norm 1, i.e., on the sphere.)
Possible representations for the rotation group: ![]() ,
, ![]() ,
quaternions of norm 1. Possible representations for the vector space:
,
quaternions of norm 1. Possible representations for the vector space:
![]() ,
, ![]() ,
, ![]() , and the space of traceless Hermitian
matrices. For
, and the space of traceless Hermitian
matrices. For ![]() with
with ![]() , the action is matrix
multiplication on the left:
, the action is matrix
multiplication on the left: ![]() . For
. For ![]() with
with ![]() , or
, or
![]() with
with ![]() or the traceless Hermitian matrices, the action is
conjugation:
or the traceless Hermitian matrices, the action is
conjugation:
![]() .
.
The actions with ![]() are all faithful. The actions with
are all faithful. The actions with ![]() are
all two-to-one:
are
all two-to-one: ![]() and
and ![]() determine the same action (i.e., rotation).
determine the same action (i.e., rotation).
Let's look at the ![]() actions in more detail. The space of traceless
Hermitian matrices consists of all matrices of the form
actions in more detail. The space of traceless
Hermitian matrices consists of all matrices of the form
![]() ,
,
![]() . This is in one-one
correspondence with
. This is in one-one
correspondence with ![]() :
:
An arbitary element ![]() of
of ![]() looks like
looks like
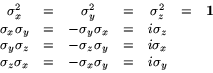
![\begin{displaymath}
\begin{array}{ccc}
\sigma_x\left[\begin{array}{c}p\\ q\end{a...
...& \left[\begin{array}{c}p\\ -q\end{array}\right]\\
\end{array}\end{displaymath}](img174.gif)
We have here non-commuting Hermitian matrices whose product is not
Hermitian-- in fact is anti-Hermitian. Now, one has an analogy between
matrices and complex numbers, under which ``Hermitian'' goes with ``real'',
``anti-Hermitian'' goes with ``purely imaginary'', and ``unitary'' goes
with ``on the unit circle''. The ![]() matrices provide a striking
example of the analogy breaking down. Non-commutativity is the culprit--
for of course the product of commuting Hermitian matrices is Hermitian.
matrices provide a striking
example of the analogy breaking down. Non-commutativity is the culprit--
for of course the product of commuting Hermitian matrices is Hermitian.
Example: what rotation does ![]() represent? Its action on the unit
x vector,
represent? Its action on the unit
x vector, ![]() , is just
, is just
![]() . Similar calculations show
that y goes to
. Similar calculations show
that y goes to ![]() y and z stays put, so we have a
y and z stays put, so we have a ![]() rotation about
the z-axis. Similarly for
rotation about
the z-axis. Similarly for ![]() and
and ![]() .
.
The exponential map provides a mapping from ![]() into
into ![]() :
:
So one can directly picture the action of ![]() on vectors in 3-space.
The ``double angles''
on vectors in 3-space.
The ``double angles'' ![]() , etc., stem from the two multiplications in
the action:
, etc., stem from the two multiplications in
the action:
![]() . And the double angles in turn are the reason
the map from
. And the double angles in turn are the reason
the map from ![]() to
to ![]() is two-to-one.
is two-to-one.
![]() acts on
acts on ![]() via left multiplication:
via left multiplication: ![]() , where
, where ![]() is a column vector. Can one picture
is a column vector. Can one picture ![]() as some kind of geometric object in 3-space? Yes indeed! An
object known as a spin vector embodies
as some kind of geometric object in 3-space? Yes indeed! An
object known as a spin vector embodies ![]() geometrically. But I
won't get to them.
geometrically. But I
won't get to them.
© 2001 Michael Weiss