We now reach a topic highlighted by Fong and Spivak: "generative effects". These are, roughly, situations where the whole is more than the sum of its parts. A nice example shows up in the logic of partitions.
Remember that any set \\(X\\) has a poset of partitions. This poset is called \\(\mathcal{E}(X)\\), and its elements are partitions of \\(X\\). Each partition \\(P\\) corresponds to an equivalence relation \\(\sim_P\\), where \\(x \sim_P y\\) if and only if \\(x\\) and \\(y\\) are in the same part of \\(P\\). This makes it easy to describe the partial order on \\(\mathcal{E}(X)\\): we say a partition \\(P\\) is **finer** than a partition \\(Q\\), or \\(Q\\) is **coarser** than \\(P\\), or simply \\(P \le Q\\), when
\[ x \sim_P y \textrm{ implies } x \sim_Q y \]
for all \\(x,y \in X\\).
Now that we have this poset, how can we do _logic_ with it?
In the logic of subsets, we've seen that "and" and "or" are the operations of "meet" and "join" in a certain poset. So, the logic of partitions should use "meet" and "join" in the poset \\(\mathcal{E}(X)\\). Let's see what they're like!
First, we can ask whether two partitions \\(P\\) and \\(Q\\) have a meet. Remember: the **meet** \\(P \wedge Q\\), if it exists, is the coarsest partition that is finer than \\(P\\) and \\(Q\\).
**Puzzle 34.** Can you draw the coarsest partition that's finer than these two partitions?
 In fact the meet of two partitions always exists, and it's easy to describe:
**Puzzle 35.** Suppose \\(P\\) and \\(Q\\) are two partitions of a set \\(X\\). Show that there's an equivalence relation \\( \approx \\) defined by
\[ x \approx y \textrm{ if and only if } x \sim_P y \textrm{ and } x \sim_Q y . \]
**Puzzle 36.** Every equivalence relation gives a partition as in [Puzzle 29](https://forum.azimuthproject.org/discussion/1963/lecture-10-the-logic-of-partitions/p1). Show that \\(\approx\\) gives the partition \\(P \wedge Q\\).
We can also ask whether \\(P\\) and \\(Q\\) have a join! The **join** \\(P \vee Q\\), if it exists, is the finest partition that is coarser than \\(P\\) and \\(Q\\).
Can you draw the finest partition that's coarser than these two partitions?
In fact the meet of two partitions always exists, and it's easy to describe:
**Puzzle 35.** Suppose \\(P\\) and \\(Q\\) are two partitions of a set \\(X\\). Show that there's an equivalence relation \\( \approx \\) defined by
\[ x \approx y \textrm{ if and only if } x \sim_P y \textrm{ and } x \sim_Q y . \]
**Puzzle 36.** Every equivalence relation gives a partition as in [Puzzle 29](https://forum.azimuthproject.org/discussion/1963/lecture-10-the-logic-of-partitions/p1). Show that \\(\approx\\) gives the partition \\(P \wedge Q\\).
We can also ask whether \\(P\\) and \\(Q\\) have a join! The **join** \\(P \vee Q\\), if it exists, is the finest partition that is coarser than \\(P\\) and \\(Q\\).
Can you draw the finest partition that's coarser than these two partitions?
 To check your answer, see our discussion of [Exercise 2](https://forum.azimuthproject.org/discussion/1872/exercise-2-chapter-1).
The join of two partitions always exists. Since "and" and "or" are meet and join in the logic of subsets, you might think the to describe the join of partitions, we just copy Puzzle 35 and replace "and" with "or". _But no!_
**Puzzle 37.** Suppose \\(P\\) and \\(Q\\) are two partitions. Show that the relation \\( \frown\\) defined by
\[ x \frown y \textrm{ if and only if } x \sim_P y \textrm{ or } x \sim_Q y \]
is _not always_ an equivalence relation.
To get the equivalence relation corresponding to \\(P \vee Q\\), we have to work harder. Say we have any partitions \\(P\\) and \\(Q\\) of some set \\(X\\). If you give me two elements \\(x, y \in X\\) and ask if they're in the same part of \\(P \vee Q\\), it's _not enough_ to check whether
\[ x \textrm{ and } y \textrm{ are in the same part of } P \textrm{ or the same part of } Q . \]
(That's what \\(x \frown y\\) means.) Instead, you have to check whether there's a _list_ of elements \\(z_1, \dots, z_n\\) such that
\[ x \textrm{ and } z_1 \textrm{ are in the same part of } P \textrm{ or the same part of } Q \]
and
\[ z_1 \textrm{ and } z_2 \textrm{ are in the same part of } P \textrm{ or the same part of } Q \]
and so on, and finally
\[ z_n \textrm{ and } y \textrm{ are in the same part of } P \textrm{ or the same part of } Q . \]
This picture by [Michael Hong](https://forum.azimuthproject.org/discussion/1855/introduction-michael-hong) shows how it works:
To check your answer, see our discussion of [Exercise 2](https://forum.azimuthproject.org/discussion/1872/exercise-2-chapter-1).
The join of two partitions always exists. Since "and" and "or" are meet and join in the logic of subsets, you might think the to describe the join of partitions, we just copy Puzzle 35 and replace "and" with "or". _But no!_
**Puzzle 37.** Suppose \\(P\\) and \\(Q\\) are two partitions. Show that the relation \\( \frown\\) defined by
\[ x \frown y \textrm{ if and only if } x \sim_P y \textrm{ or } x \sim_Q y \]
is _not always_ an equivalence relation.
To get the equivalence relation corresponding to \\(P \vee Q\\), we have to work harder. Say we have any partitions \\(P\\) and \\(Q\\) of some set \\(X\\). If you give me two elements \\(x, y \in X\\) and ask if they're in the same part of \\(P \vee Q\\), it's _not enough_ to check whether
\[ x \textrm{ and } y \textrm{ are in the same part of } P \textrm{ or the same part of } Q . \]
(That's what \\(x \frown y\\) means.) Instead, you have to check whether there's a _list_ of elements \\(z_1, \dots, z_n\\) such that
\[ x \textrm{ and } z_1 \textrm{ are in the same part of } P \textrm{ or the same part of } Q \]
and
\[ z_1 \textrm{ and } z_2 \textrm{ are in the same part of } P \textrm{ or the same part of } Q \]
and so on, and finally
\[ z_n \textrm{ and } y \textrm{ are in the same part of } P \textrm{ or the same part of } Q . \]
This picture by [Michael Hong](https://forum.azimuthproject.org/discussion/1855/introduction-michael-hong) shows how it works:
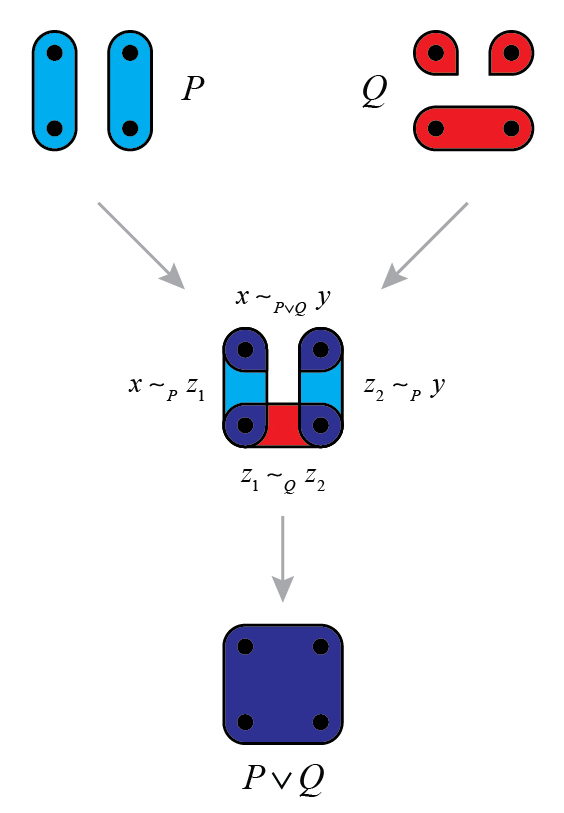 So, the join is a lot more complicated than the meet!
**Puzzle 38.** If \\(P\\) and \\(Q\\) are two partitions on a set \\(X\\), let the relation \\( \simeq \\) be the **[transitive closure](https://en.wikipedia.org/wiki/Transitive_closure)** of the relation \\( \frown \\) defined in Puzzle 37. This means that \\( x \simeq y\\) if and only if
\[ x \frown z_1 \textrm{ and } z_1 \frown z_2 \textrm{ and } \dots \textrm{ and } z_{n-1} \frown z_n \textrm{ and } z_n \frown y \]
for some \\(z_1, \dots, z_n \in X\\). Show that \\( \simeq \\) is an equivalence relation.
**Puzzle 39.** Show that the equivalence relation \\( \simeq \\) on \\(X\\) gives the partition \\(P \vee Q \\).
This is the first hint of what Fong and Spivak call a "generative effect". To decide if two elements \\(x , x' \in X\\) are in the same part of the meet \\(P \wedge Q\\), it's enough to know if they're the same part of \\(P\\) and the same part of \\(Q\\), since
\[ x \sim_{P \wedge Q} x' \textrm{ if and only if } x \sim_P x' \textrm{ and } x \sim_Q x'. \]
But this does _not_ work for the join!
\[ \textbf{THIS IS FALSE: } \; x \sim_{P \vee Q} x' \textrm{ if and only if } x \sim_P x' \textrm{ or } x \sim_Q x' . \]
To decide if \\(x \sim_{P \vee Q} y\\) you need to look at _other_ elements of \\(X\\), too. It's not a "local" calculation - it's a "global" one!
But to make this really precise and clear, we need to think about "pulling back" partitions. We'll do that next time.
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Course)**
So, the join is a lot more complicated than the meet!
**Puzzle 38.** If \\(P\\) and \\(Q\\) are two partitions on a set \\(X\\), let the relation \\( \simeq \\) be the **[transitive closure](https://en.wikipedia.org/wiki/Transitive_closure)** of the relation \\( \frown \\) defined in Puzzle 37. This means that \\( x \simeq y\\) if and only if
\[ x \frown z_1 \textrm{ and } z_1 \frown z_2 \textrm{ and } \dots \textrm{ and } z_{n-1} \frown z_n \textrm{ and } z_n \frown y \]
for some \\(z_1, \dots, z_n \in X\\). Show that \\( \simeq \\) is an equivalence relation.
**Puzzle 39.** Show that the equivalence relation \\( \simeq \\) on \\(X\\) gives the partition \\(P \vee Q \\).
This is the first hint of what Fong and Spivak call a "generative effect". To decide if two elements \\(x , x' \in X\\) are in the same part of the meet \\(P \wedge Q\\), it's enough to know if they're the same part of \\(P\\) and the same part of \\(Q\\), since
\[ x \sim_{P \wedge Q} x' \textrm{ if and only if } x \sim_P x' \textrm{ and } x \sim_Q x'. \]
But this does _not_ work for the join!
\[ \textbf{THIS IS FALSE: } \; x \sim_{P \vee Q} x' \textrm{ if and only if } x \sim_P x' \textrm{ or } x \sim_Q x' . \]
To decide if \\(x \sim_{P \vee Q} y\\) you need to look at _other_ elements of \\(X\\), too. It's not a "local" calculation - it's a "global" one!
But to make this really precise and clear, we need to think about "pulling back" partitions. We'll do that next time.
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Course)**


