Before we dive into the math of resource theories, let me say a bit more about what they're good for! I said they're good for answering questions like these:
1. Given what I have, _is it possible_ to get what I want?
2. Given what I have, _how much will it cost_ to get what I want?
3. Given what I have, _how long will it take_ to get what I want?
4. Given what I have, _what is the set of ways_ to get what I want?
and also others. But let's see examples!
**Chemistry.** Suppose we have a bunch of chemicals, and reactions involving these chemicals. Then we can ask which collections of molecules can turn into which other collections. We can also ask what's the set of ways in which this can happen.
**Puzzle 55.** For example, suppose you have these chemical reactions:
\[ \text{C} + \text{O}_2 \longrightarrow \text{CO}_2 \]
\[ \text{CO}_2 + \text{NaOH} \longrightarrow \text{NaHCO}_3 \]
\[ \text{NaHCO}_3 + \text{HCl} \longrightarrow \text{H}_2 \text{O} + \text{NaCl} + \text{CO}_2 \]
Can you use these to turn
\[ \text{C} + \text{O}_2 + \text{NaOH} + \text{HCl} \]
into
\[ \text{CO}_2 + \text{H}_2\text{O} + \text{NaCl} \text{?} \]
If so, how many ways can you do it?
The "can you do it?" question here is called the **reachability problem**, and you can read about it here:
* John Baez and Jacob Biamonte, _[Quantum Techniques for Stochastic Mechanics](https://arxiv.org/abs/1209.3632)_, Section 25.1: The Reachability Problem, World Scientific Press, 2018.
If you like hard problems, the reachability problem is for you! The puzzle above is not hard, but in general the reachability problem is very hard. It was proved in 1981 that there's an algorithm to solve it, no matter what chemicals and reactions you choose. In other words, it's ["decidable"](https://en.wikipedia.org/wiki/Decidability_(logic)). However, it's known that no algorithm can solve it in [polynomial time](https://en.wikipedia.org/wiki/Time_complexity#Polynomial_time). The only known _upper bound_ on the runtime of an algorithm that solves the reachability problem is insanely bad... in fact, so bad that I'll make you read our book to learn how bad! So, there's a very interesting set of puzzles here for people skilled in [computational complexity theory](https://en.wikipedia.org/wiki/Computational_complexity_theory).
One way to draw a bunch of chemicals and reactions involving them is a ["Petri net"](https://en.wikipedia.org/wiki/Petri_net). Here's the Petri net for the reactions I just listed:
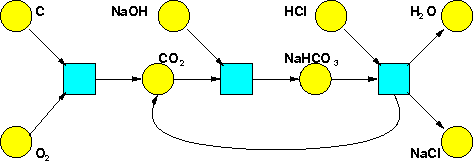 My book with Jacob is really about Petri nets. They're actually used in computer science more than chemistry! That's because they're a good way to draw a bunch of processes that take certain inputs and produce a bunch of outputs. Whenever we have this sort of situation, the reachability problem becomes important.
**Scheduling.** Suppose you have a bunch of jobs to do, that take various amounts of time. And suppose you can only start some jobs when others are done. How long will it take to do all these jobs?
This a hugely important problem, for example in big companies. One approach to solving it uses ["PERT charts"](https://en.wikipedia.org/wiki/Program_evaluation_and_review_technique), where "PERT" - businesspeople love acronyms but I hate them - stands for "program evaluation and review technique". Here's an example:
My book with Jacob is really about Petri nets. They're actually used in computer science more than chemistry! That's because they're a good way to draw a bunch of processes that take certain inputs and produce a bunch of outputs. Whenever we have this sort of situation, the reachability problem becomes important.
**Scheduling.** Suppose you have a bunch of jobs to do, that take various amounts of time. And suppose you can only start some jobs when others are done. How long will it take to do all these jobs?
This a hugely important problem, for example in big companies. One approach to solving it uses ["PERT charts"](https://en.wikipedia.org/wiki/Program_evaluation_and_review_technique), where "PERT" - businesspeople love acronyms but I hate them - stands for "program evaluation and review technique". Here's an example:
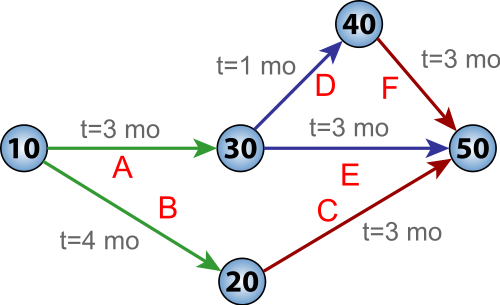 The circles are different **states**, while the edges are different **tasks**. Each state is labelled with an arbitrary name: 10, 20, 30, 40 and 50. The tasks also have names: A, B, C, D, E, and F. More importantly, each task is labelled by the amount of time that task requires!
Your goal is to start at state 10 and move all the way to state 50. Since you're bossing lots of people around, you can make them do tasks simultaneously. However, you can only reach a state after you have done _all_ the tasks leading up to that state. For example, you can't reach state 50 unless you have already done _all_ of tasks C, E, and F.
**Puzzle 56.** What is the minimum amount of time it takes to get from state 10 to state 50?
**Puzzle 57.** Which tasks could take longer, without changing the answer to Puzzle 56? How much longer could each task take, without changing the answer? This amount of time is called the **slack** for that task.
For an introduction to PERT charts and their uses, see:
* Wikipedia, [Program evaluation and review technique](https://en.wikipedia.org/wiki/Program_evaluation_and_review_technique).
* Wikipedia, [Critical path method](https://en.wikipedia.org/wiki/Critical_path_method).
You can read about algorithms to solve puzzles like those above: companies use the algorithms to schedule tasks! And so do governments. It's used to simplify the scheduling of large and complex projects - first in 1957 by the U.S. Navy, but later all over industry. For example, in 1968 it was used to help plan the Olympics.
As a category theorist, I am immediately attracted to _diagrams_, so I loved Petri nets and PERT charts as soon as I saw them. The puzzle for me was then to figure out the category theory hiding behind these diagrams!
I think I understand some things now. For example, it's possible to reinterpret PERT charts as "timed" Petri nets: that is, Petri nets where each reaction takes a specific amount of time.
But I haven't figured out everything. It's all part of a big subject: _resource theories!_
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_2)**
The circles are different **states**, while the edges are different **tasks**. Each state is labelled with an arbitrary name: 10, 20, 30, 40 and 50. The tasks also have names: A, B, C, D, E, and F. More importantly, each task is labelled by the amount of time that task requires!
Your goal is to start at state 10 and move all the way to state 50. Since you're bossing lots of people around, you can make them do tasks simultaneously. However, you can only reach a state after you have done _all_ the tasks leading up to that state. For example, you can't reach state 50 unless you have already done _all_ of tasks C, E, and F.
**Puzzle 56.** What is the minimum amount of time it takes to get from state 10 to state 50?
**Puzzle 57.** Which tasks could take longer, without changing the answer to Puzzle 56? How much longer could each task take, without changing the answer? This amount of time is called the **slack** for that task.
For an introduction to PERT charts and their uses, see:
* Wikipedia, [Program evaluation and review technique](https://en.wikipedia.org/wiki/Program_evaluation_and_review_technique).
* Wikipedia, [Critical path method](https://en.wikipedia.org/wiki/Critical_path_method).
You can read about algorithms to solve puzzles like those above: companies use the algorithms to schedule tasks! And so do governments. It's used to simplify the scheduling of large and complex projects - first in 1957 by the U.S. Navy, but later all over industry. For example, in 1968 it was used to help plan the Olympics.
As a category theorist, I am immediately attracted to _diagrams_, so I loved Petri nets and PERT charts as soon as I saw them. The puzzle for me was then to figure out the category theory hiding behind these diagrams!
I think I understand some things now. For example, it's possible to reinterpret PERT charts as "timed" Petri nets: that is, Petri nets where each reaction takes a specific amount of time.
But I haven't figured out everything. It's all part of a big subject: _resource theories!_
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_2)**

