I'm going to end my [lectures on Chapter 2](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_2) now, since my plan is to spend three weeks on each chapter, and I'm eager to tell you about _categories_ - the subject of the next chapter!
There are a few loose ends I'd like to tie up, though.
One is a trick for building \\(\mathrm{Cost}\\)-categories from pictures like this:
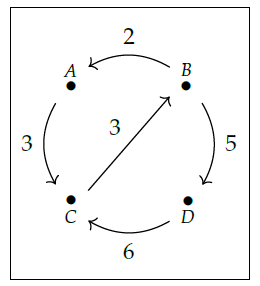 This is called a **\\(\mathbf{Cost}\\)-weighted graph** since it's a graph with edges labeled by costs. You can think of the vertices of the graph as cities, and the edges as ways to get from one city to another. Each of these ways has a cost.
Here's how we build a \\(\mathrm{Cost}\\)-category \\(\mathcal{X}\\) from this data. We take \\(\mathrm{Ob}(\mathcal{X})\\), the set of objects of \\(\mathcal{X}\\), to be the the set of vertices of our graph. For each pair of vertices \\(x,y\\) we then need to choose a cost \\(\mathcal{X}(x,y)\\). To do this, we find the cost of the cheapest path from \\(x\\) to \\(y\\). Here a "path" is a sequence of edges in our graph, each starting where the last one ended. The "cost" of a path is the sum of the costs of all the edges in this path.
For example, in the picture above there are exactly two paths from \\(B\\) to \\(C\\). One goes from \\(B\\) to \\(A\\) to \\(C\\) and its cost is \\(2 + 3 = 5\\). The other goes from \\(B\\) to \\(D\\) to \\(C\\) and its cost is \\(5 + 6 = 11\\). So,
$$ \mathcal{X}(B, C) = 5 . $$
All this should be familiar if you often travel, paying fares for planes, trains, buses and taxis. The nice thing is that this recipe really obeys the two rules of a \\(\mathrm{Cost}\\)-category! We have
$$ \mathcal{X}(x,x) = 0 $$
since to get from \\(x\\) to itself we can always use the path with no edges, which has cost \\(0\\). We also have the triangle inequality
$$ \mathcal{X}(x,z) \le \mathcal{X}(x,y) + \mathcal{X}(y,z) $$
since _one_ way to get from \\(x\\) to \\(z\\) is to take the cheapest path from \\(x\\) to \\(y\\) and then the cheapest path from \\(y\\) to \\(z\\).
I'm being quick and sloppy here, but you can see more details in Section 2.3.3 of the book.
**Puzzle 93.** How should we define \\(\mathcal{X}(x,y)\\) when there is no path from \\(x\\) to \\(y\\)? How can we define \\(\mathcal{X}(x,y)\\), more rigorously than I've done, yet also very simply, so that this case is not an "exception"?
We can generalize this whole story, replacing \\(\mathbf{Cost}\\) by any [unital commutative quantale](https://en.wikipedia.org/wiki/Quantale). These are a very nice kind of symmetric monoidal poset - another example is our friend \\(\mathbf{Bool}\\). You can read about them in Section 2.5 of the book. When \\(\mathcal{V}\\) is one of these, you can build a \\(\mathcal{V}\\)-category from any \\(\mathcal{V}\\)-weighted graph, and the book gives a nice algorithm for doing it.
One other loose end involves maps between enriched categories. I explained [last time](https://forum.azimuthproject.org/discussion/2169/lecture-32-chapter-2-enriched-functors/p1) what a map between two \\(\mathcal{V}\\)-categories is like - it's called a \\(\mathcal{V}\\)-functor. But I didn't tell you how to map a \\(\mathcal{V}\\)-category to a \\(\mathcal{W}\\)-category! You can only do this when we have a map from \\(\mathcal{V}\\) to \\(\mathcal{W}\\).
This involves a beautiful trick called **change of base**.
**Puzzle 94.** Suppose \\(\mathcal{V}\\) and \\(\mathcal{W}\\) are monoidal posets and \\(f: \mathcal{V} \to \mathcal{W}\\) is a monoidal monotone. Suppose \\(\mathcal{X}\\) is a \\(\mathcal{V}\\)-category. Show how to construct a \\(\mathcal{W}\\)-category \\(\mathcal{X}_f\\) with the same objects as \\(\mathcal{X}\\) and
\[ \mathcal{X}_f(x,x') = f(\mathcal{X}(x,x')) \]
for all objects \\(x,x'\\). Hint: follow your nose, don't do anything fancy.
Once you've done this, you can map your \\(\mathcal{V}\\)-category \\(\mathcal{X}\\) to a \\(\mathcal{W}\\)-category \\(\mathcal{Y}\\). First you use change of base to turn \\(\mathcal{X}\\) into a \\(\mathcal{W}\\)-category \\(\mathcal{X}_f\\), and then you pick a \\(\mathcal{W}\\)-functor
\[ F : \mathcal{X}_f \to \mathcal{Y} .\]
In short: first you move \\(\mathcal{X}\\) to the world where \\(\mathcal{Y}\\) lives, and then it can talk to \\(\mathcal{Y}\\)!
To understand the usefulness of this, you need to see examples. I'll get you started here:
**Puzzle 95.** Show that there is a monoidal monotone \\(f : \mathbf{Cost} \to \mathbf{Bool} \\) sending \\(\infty\\) to \\(\texttt{false}\\) everything else to \\(\texttt{true}\\). In economics, this means "if the cost of something is infinite, nobody can do it - otherwise it's possible, at least if you're rich enough".
**Puzzle 96.** Take this \\(\mathbf{Cost}\\)-graph
This is called a **\\(\mathbf{Cost}\\)-weighted graph** since it's a graph with edges labeled by costs. You can think of the vertices of the graph as cities, and the edges as ways to get from one city to another. Each of these ways has a cost.
Here's how we build a \\(\mathrm{Cost}\\)-category \\(\mathcal{X}\\) from this data. We take \\(\mathrm{Ob}(\mathcal{X})\\), the set of objects of \\(\mathcal{X}\\), to be the the set of vertices of our graph. For each pair of vertices \\(x,y\\) we then need to choose a cost \\(\mathcal{X}(x,y)\\). To do this, we find the cost of the cheapest path from \\(x\\) to \\(y\\). Here a "path" is a sequence of edges in our graph, each starting where the last one ended. The "cost" of a path is the sum of the costs of all the edges in this path.
For example, in the picture above there are exactly two paths from \\(B\\) to \\(C\\). One goes from \\(B\\) to \\(A\\) to \\(C\\) and its cost is \\(2 + 3 = 5\\). The other goes from \\(B\\) to \\(D\\) to \\(C\\) and its cost is \\(5 + 6 = 11\\). So,
$$ \mathcal{X}(B, C) = 5 . $$
All this should be familiar if you often travel, paying fares for planes, trains, buses and taxis. The nice thing is that this recipe really obeys the two rules of a \\(\mathrm{Cost}\\)-category! We have
$$ \mathcal{X}(x,x) = 0 $$
since to get from \\(x\\) to itself we can always use the path with no edges, which has cost \\(0\\). We also have the triangle inequality
$$ \mathcal{X}(x,z) \le \mathcal{X}(x,y) + \mathcal{X}(y,z) $$
since _one_ way to get from \\(x\\) to \\(z\\) is to take the cheapest path from \\(x\\) to \\(y\\) and then the cheapest path from \\(y\\) to \\(z\\).
I'm being quick and sloppy here, but you can see more details in Section 2.3.3 of the book.
**Puzzle 93.** How should we define \\(\mathcal{X}(x,y)\\) when there is no path from \\(x\\) to \\(y\\)? How can we define \\(\mathcal{X}(x,y)\\), more rigorously than I've done, yet also very simply, so that this case is not an "exception"?
We can generalize this whole story, replacing \\(\mathbf{Cost}\\) by any [unital commutative quantale](https://en.wikipedia.org/wiki/Quantale). These are a very nice kind of symmetric monoidal poset - another example is our friend \\(\mathbf{Bool}\\). You can read about them in Section 2.5 of the book. When \\(\mathcal{V}\\) is one of these, you can build a \\(\mathcal{V}\\)-category from any \\(\mathcal{V}\\)-weighted graph, and the book gives a nice algorithm for doing it.
One other loose end involves maps between enriched categories. I explained [last time](https://forum.azimuthproject.org/discussion/2169/lecture-32-chapter-2-enriched-functors/p1) what a map between two \\(\mathcal{V}\\)-categories is like - it's called a \\(\mathcal{V}\\)-functor. But I didn't tell you how to map a \\(\mathcal{V}\\)-category to a \\(\mathcal{W}\\)-category! You can only do this when we have a map from \\(\mathcal{V}\\) to \\(\mathcal{W}\\).
This involves a beautiful trick called **change of base**.
**Puzzle 94.** Suppose \\(\mathcal{V}\\) and \\(\mathcal{W}\\) are monoidal posets and \\(f: \mathcal{V} \to \mathcal{W}\\) is a monoidal monotone. Suppose \\(\mathcal{X}\\) is a \\(\mathcal{V}\\)-category. Show how to construct a \\(\mathcal{W}\\)-category \\(\mathcal{X}_f\\) with the same objects as \\(\mathcal{X}\\) and
\[ \mathcal{X}_f(x,x') = f(\mathcal{X}(x,x')) \]
for all objects \\(x,x'\\). Hint: follow your nose, don't do anything fancy.
Once you've done this, you can map your \\(\mathcal{V}\\)-category \\(\mathcal{X}\\) to a \\(\mathcal{W}\\)-category \\(\mathcal{Y}\\). First you use change of base to turn \\(\mathcal{X}\\) into a \\(\mathcal{W}\\)-category \\(\mathcal{X}_f\\), and then you pick a \\(\mathcal{W}\\)-functor
\[ F : \mathcal{X}_f \to \mathcal{Y} .\]
In short: first you move \\(\mathcal{X}\\) to the world where \\(\mathcal{Y}\\) lives, and then it can talk to \\(\mathcal{Y}\\)!
To understand the usefulness of this, you need to see examples. I'll get you started here:
**Puzzle 95.** Show that there is a monoidal monotone \\(f : \mathbf{Cost} \to \mathbf{Bool} \\) sending \\(\infty\\) to \\(\texttt{false}\\) everything else to \\(\texttt{true}\\). In economics, this means "if the cost of something is infinite, nobody can do it - otherwise it's possible, at least if you're rich enough".
**Puzzle 96.** Take this \\(\mathbf{Cost}\\)-graph
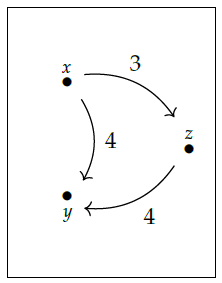 turn it into a \\(\mathbf{Cost}\\)-category \\(\mathcal{X}\\), and then use change of base to create the \\(\mathbf{Bool}\\)-category \\(\mathcal{X}_f\\). Describe \\(\mathcal{X}_f\\) in detail and also say what it means in terms of travel routes!
I also feel bad because I didn't get as deep into some applications as I'd like - for example, Tobias Fritz's theorems justifying the use of _real numbers_ to measure the value of resources in some cases (but not in others). I'd be happy to talk about them in our discussions, though! You can get started by reading these blog articles:
* Tobias Fritz, [Resource convertibility (part 1)](https://johncarlosbaez.wordpress.com/2015/04/07/resource-convertibility-part-1/), _Azimuth_, 7 April 2015.
* Tobias Fritz, [Resource convertibility (part 2)](https://johncarlosbaez.wordpress.com/2015/04/10/resource-convertibility-part-2/), _Azimuth_, 10 April 2015.
* Tobias Fritz, [Resource convertibility (part 3)](https://johncarlosbaez.wordpress.com/2015/04/13/resource-convertibility-part-3/), _Azimuth_, 13 April 2015.
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_2)**
turn it into a \\(\mathbf{Cost}\\)-category \\(\mathcal{X}\\), and then use change of base to create the \\(\mathbf{Bool}\\)-category \\(\mathcal{X}_f\\). Describe \\(\mathcal{X}_f\\) in detail and also say what it means in terms of travel routes!
I also feel bad because I didn't get as deep into some applications as I'd like - for example, Tobias Fritz's theorems justifying the use of _real numbers_ to measure the value of resources in some cases (but not in others). I'd be happy to talk about them in our discussions, though! You can get started by reading these blog articles:
* Tobias Fritz, [Resource convertibility (part 1)](https://johncarlosbaez.wordpress.com/2015/04/07/resource-convertibility-part-1/), _Azimuth_, 7 April 2015.
* Tobias Fritz, [Resource convertibility (part 2)](https://johncarlosbaez.wordpress.com/2015/04/10/resource-convertibility-part-2/), _Azimuth_, 10 April 2015.
* Tobias Fritz, [Resource convertibility (part 3)](https://johncarlosbaez.wordpress.com/2015/04/13/resource-convertibility-part-3/), _Azimuth_, 13 April 2015.
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_2)** 

