Chapter 3 of _[Seven Sketches](http://math.mit.edu/~dspivak/teaching/sp18/7Sketches.pdf)_ is about databases, which are a great excuse to finally introduce the main theme of this course: _categories!_   

So, with no further ado:

**Definition.**  A **category** \\(\mathcal{C}\\) consists of:

1.  a collection \\(\mathrm{Ob}(\mathcal{C})\\), elements of which are called **objects**;

2.  for each pair of objects \\(c,c'\\), a set \\(\mathcal{C}(c,c')\\).   Elements of this set are called **morphisms from \\(c\\) to \\(c'\\)**.    If \\(f\\) is a morphism from \\(c\\) to \\(c'\\) we write \\(f: c \to c'\\).   

Furthermore:

a) given morphisms \\(f : c \to c'\\) and \\(g : c' \to c''\\) there is a morphism \\(g \circ f : c \to c''\\) called the **composite** of \\(f\\) and \\(g\\);

b) given any object \\(c\\) there is a morphism \\(1_c : c \to c\\) called the **identity morphism** of \\(c\\).

Finally, we require that these laws hold:

i) the **associative law**: \\(h \circ (g \circ f)  = (h \circ g) \circ f\\) holds for any morphisms \\(f: c \to c', g: c' \to c'', h: c'' \to c'''\\);

ii) the **left and right unit laws**: \\(1_{c'} \circ f = f = f \circ 1_c \\) holds for any morphism \\(f : c \to c'\\).

To understand all this, it's important to know a bunch of examples.  I'll start you out with two, and make you come up with some others in some puzzles.

First, _every preorder gives a category!_  This is why we spent so much time on preorders.  

Suppose we have a preorder \\( (X, \le ) \\).  Here's how to build a category \\(\mathcal{C}\\).  Take the objects of \\(\mathcal{C}\\) to be the elements of \\(X\\), and let \\(C\\) have exactly one morphism from \\(x\\) to \\(y\\) when \\(x \le y\\), and none otherwise.  Then there is just one way to define composition and identity morphisms to create a category!

To see this, notice:

a) Given morphisms  \\(f : x \to x'\\) and \\(g : x' \to x''\\) in \\(\mathcal{C}\\), we must have \\(x \le x'\\) and \\(x' \le x''\\), so by transitivity we have \\(x \le x''\\).  Thus, there is exactly one morphism \\(h: x \to x''\\), so we have to define \\(g \circ f = h\\).   So, _transitivity gives composition, without any choice about how to do it!_

b) Given an object \\(x\\), we must have \\(x \le x\\), by reflexivity.   Thus, there is exactly one morphism \\(f: x \to x\\), so we have to define \\(1_x = f\\).   So, _reflexivity gives identity morphisms, without any choice about how to do it!_

Then:

i) The associative law is automatic: for any morphisms \\(f: x \to x', g: x' \to x'', h: x'' \to x'''\\), we must have \\(h \circ (g \circ f)  = (h \circ g) \circ f\\) because there's at most one morphism from \\(x\\) to \\(x''\\).

ii) The left and right unit laws are automatic: for any morphism \\(f: x \to x'\\) we must have \\(1_{x'} \circ f = f = f \circ 1_x\\) because there's at most one morphism from \\(x\\) to \\(x'\\).  

So, preorders give rise to a very special sort of category: a category where there's at most one morphism \\(f : c \to c'\\) from any object \\(c\\) to any object \\(c'\\)   Conversely, you can turn around the argument I just made and show that any category of this sort comes from a preorder!

So, you know lots of categories: all the preorders you know give examples of categories.   And in fact, everything we've done so far is a special case of something one can do with categories!   

So let's look at an example of another sort.   There's a category \\(\mathbf{Set}\\) where:

1.  the objects of \\(\mathbf{Set}\\) are sets;

2.  if \\(S,S'\\) are sets, a morphism \\(f: S \to S'\\) is a function from \\(S\\) to \\(S'\\).

To make this into a category, we need to define composition and identity morphisms.
 
a) Given functions \\(f : S \to S'\\) and \\(g : S' \to S''\\), the composite function \\(g \circ f : S \to S''\\) is defined in the usual way:

\[    (g \circ f)(x) = g(f(x))  \]

for all \\(x \in S\\).

b) Given any set \\(S\\),  the identity function \\(1_S : S \to S\\) is defined in the usual way:

\[    1_S (x) = x \]

for all \\(x \in S\\).

It's easy to check the associative law and the left and right unit laws - if you haven't done this before, you've gotta do now!

Notice that this category \\(\mathbf{Set}\\) is not a preorder, because in this category there are usually _lots_ of morphisms from one object to another.

Okay, let's conclude with a few puzzles.

**Puzzle 97.**  How many different categories are there with exactly 4 morphisms?   

**Puzzle 98.**   What does a category with exactly one object amount to?   It's something we've already discussed!

**Puzzle 99.**  There is a category whose only object \\(x\\) is this picture:

<center><img width = "120" src = "http://math.ucr.edu/home/baez/mathematical/7_sketches/square.png"></center>

with morphisms \\(f : x \to x\\) being all the ways of rotating and/or reflecting this picture to get the same picture, and with composition and the identity morphism defined in the obvious way.    How many morphisms are there in this category?   Is this category a preorder?

**Puzzle 100.**  There is a category with these 8 pictures as objects:

<center><img src = "http://math.ucr.edu/home/baez/mathematical/7_sketches/square_groupoid.png"></center>

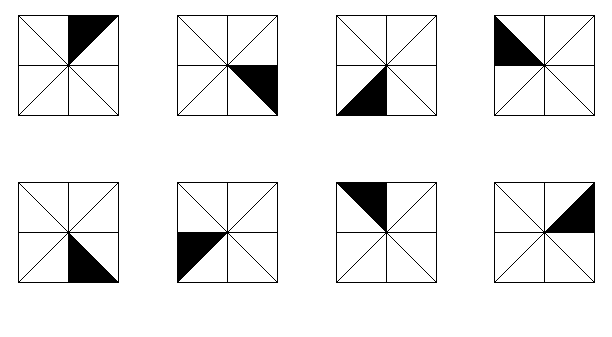and all ways of rotating and/or reflecting a picture \\(x\\) to get a picture \\(y\\) as morphisms \\(f : x \to y\\), with composition and identities defined in the obvious way.    How many morphisms are there in this category?   Is this category a preorder?

**Puzzle 101.**  There are certain sets \\(S\\) such that there's at most one function from any set to \\(S\\) and also at most one function from \\(S\\) to any set.   If we take sets of this sort and functions between them, we get a "subcategory" of \\(\mathbf{Set}\\) that's actually a preorder.   What is this preorder like?

**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_3)**